Exercice 01-02
Montrer que chaque fonction ci-dessous est bijective, et donner sa réciproque.
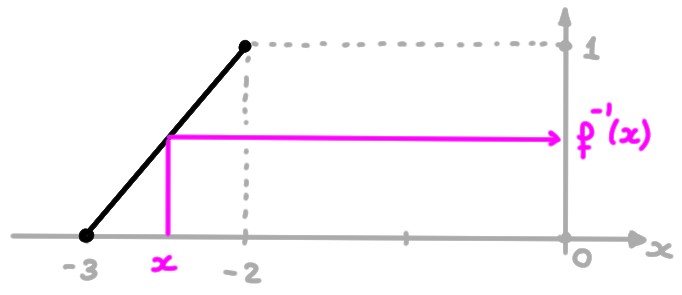
  1. \(f:[0,1]\to [-3,-2]\), \(f(x)=x-3\).
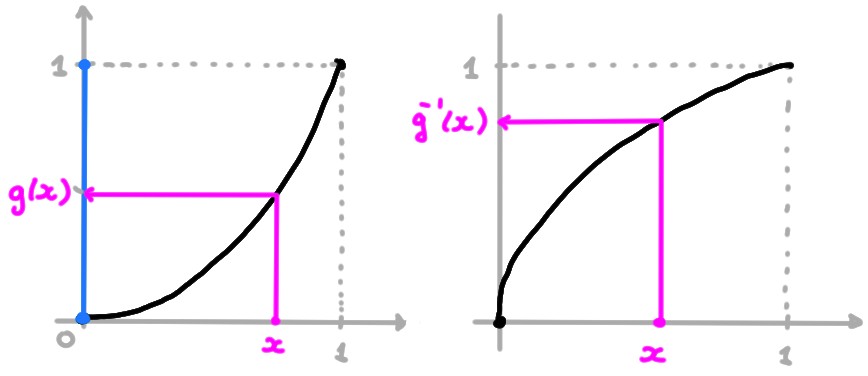
  2. \(g:[0,1]\to [0,1]\), \(g(x)=x^2\).
  3. \(h:[-1,0]\to [0,1]\), \(h(x)=x^2\).
Ensuite, esquisser le graphe de chacune de ces fonctions, ainsi que de leurs réciproques.
Rappelons qu'une fonction est bijective si elle est à la fois injective et bijective. Voir ici pour le cas des fonctions réelles.

Dans cet exercice, il s'agit d'entraîner les définitions, et de les mettre à l'oeuvre dans des cas simples concrets. Quelques points qu'il faut bien maîtriser:

il faut montrer que si \(x,x'\in A\) sont tels que \(f(x)=f(x')\), alors ceci entraîne que \(x=x'\).

il faut montrer que pour tout \(y\in B\), il existe au moins un \(x\in A\) tel que \(f(x)=y\).

l'unique fonction \(f^{-1}:B\to A\) telle que \(y=f(x)\) si et seulement si \(x=f^{-1}(y)\).

en réfléchissant celui de \(f\) à travers la diagonale (c'est-à-dire la droite d'équation \(y=x\)).

Remarque: Cet exercice fait usage de la fonction ''racine carrée'', qui ne sera construite que plus tard dans le cours.

Sur les images ci-dessous, l'ensemble image d'une fonction est toujours représenté en bleu.
  1. On peut commencer par remarquer que le problème est bien posé, puisque les images des \(x\in [0,1]\) par \(f(x)=x-3\) sont bien toutes dans \([-3,-2]\).
    Soient \(x,x'\in [0,1]\) tels que \(f(x)=f(x')\), c'est-à-dire tels que \(x-3=x'-3\). Comme ceci implique (on fait ''\(+3\)'' des deux côtés) que \(x=x'\), ceci montre que \(f\) est injective.

    Fixons ensuite un \(y\in [-3,-2]\), et considérons l'équation \(y=f(x)\), c'est-à-dire \(y=x-3\). Puisque cette dernière peut s'écrire \(x=y+3\), on a bien trouvé une préimage (ce \(x\) là) pour \(y\). Il faut encore vérifier que \(x\in [0,1]\). Or, puisque \(-3\leqslant y\leqslant -2\), on a \(0\leqslant y+3\leqslant 1\), c'est-à-dire \(x\in [0,1]\). Ceci montre que \(f\) est surjective.

    Donc \(f\) est bijective. Sa réciproque s'obtient en fixant \(y\in [-3,-2]\) et en exprimant explicitement l'unique \(x\) tel que \(y=f(x)=x-3\). Or comme \(x=y+3\), on a que \(f^{-1}(y)=y+3\). Donc la réciproque est \(f^{-1}:[-3,-2]\to [0,1]\), donnée par \(f^{-1}(x)=x+3\).
  2. On peut commencer par remarquer que le problème est bien posé, puisque les images des \(x\in [0,1]\) par \(f(x)=x^2\) sont bien toutes dans \([0,1]\). Soient \(x,x'\in [0,1]\) tels que \(g(x)=g(x')\), c'est-à-dire tels que \(x^2={x'}^2\). Remarquons que ceci implique \(x^2-{x'}^2=0\), qui est équivalent à \[ (x-x')(x+x')=0\,. \] Pour que ce dernier produit soit nul, au moins une des parenthèses doit être nulle. Or la deuxième ne peut être nulle que si \(x=x'=0\) (on rappelle que \(x,x'\) sont tous les deux dans \([0,1]\)). Et la première ne peut être nulle que si \(x=x'\). On a donc bien que \(g(x)=g(x')\Rightarrow x=x'\): \(f\) est injective.

    On verra au cours que si on fixe \(y\in[0,1]\), alors il existe \(x\in [0,1]\) tel que que \(g(x)=x^2=y\).

    Ainsi, \(g:[0,1]\to[0,1]\) est bijective, et possède une réciproque \(g^{-1}:[0,1]\to[0,1]\). On la note \(g^{-1}(y)=\sqrt{y}\), et on l'appelle racine carrée.
  3. On montre comme au point précédent que \(h\) est injective. Pour montrer qu'elle est surjective, fixons \(y\in [0,1]\). Si on pose \(x:= -\sqrt{y}\) (''\(\sqrt{\phantom{y}}\)'' étant la racine carrée du point précédent), on remarque que \[ x^2=(-\sqrt{y})^2=\sqrt{y}^2=y\,, \] donc \(x\) est préimage de \(y\). Ceci montre que \(h\) est surjective.

    Ainsi, \(h\) est bijective, et sa réciproque n'est autre que \(h^{-1}:[0,1]\to[-1,0]\), \(h^{-1}(y)=-\sqrt{y}\).