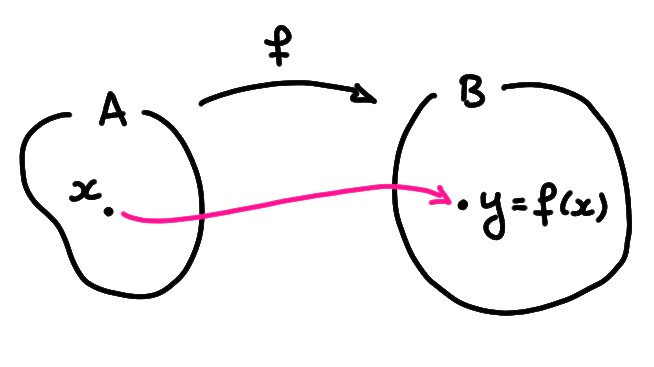
Dans cette section, on rappelle quelques définitions élémentaires relatives à la notion de fonction. Même si dans ce cours on s'intéressera surtout à des fonctions réelles d'une variable réelle, ce que l'on présente ici est très général et s'applique à des situations très diverses, comme par exemple l'étude des applications linéaires en algèbre linéaire.
Lorsque \(x\in A\) est associé à \(y\in B\), on pourra penser à cette association comme à une ''flèche de \(x\) vers \(y\)''. En termes de flèches, une fonction de \(A\) dans \(B\) est donc bien définie une fois que l'on a, pour chaque \(x\in A\), exactement une flèche reliant ce \(x\) à un (et un seul) \(y\in B\). En particulier, il ne peut pas y avoir deux flèches sortant d'un \(x\).
Pour des raisons évidentes, \(A\) est parfois appelé l'ensemble de départ, et \(B\) l'ensemble d'arrivée. Pour bien indiquer l'ensemble de départ et d'arrivée d'une fonction, on écrit \[\begin{aligned} f:A& \to B\\ x&\mapsto y=f(x)\,. \end{aligned}\]
Exemple: Considérons \(A=\mathbb{Z}\), \(B=\{\bigstar,\clubsuit,\spadesuit,\blacklozenge\}\), et définissons la fonction \(f:A\to B\) comme suit: pour \(x\in A\), \[ f(x):= \begin{cases} \bigstar&\text{ si }x\leqslant -17\,,\\ \clubsuit&\text{ si }-17\lt x \lt -16 \,,\\ \spadesuit&\text{ si }-16\leqslant x \leqslant 1 \,,\\ \blacklozenge&\text{ si } x\gt 1 \,. \end{cases} \] Ici, \(\bigstar\) et \(\blacklozenge\) possèdent chacun une infinité de préimages, \(\spadesuit\) possède \(18\) préimages, et \(\clubsuit\) ne possède aucune préimage.
Il est naturel de considérer, pour commencer l'étude d'une fonction, de déterminer quels sont les éléments de l'ensemble d'arrivée qui possèdent au moins une préimage:
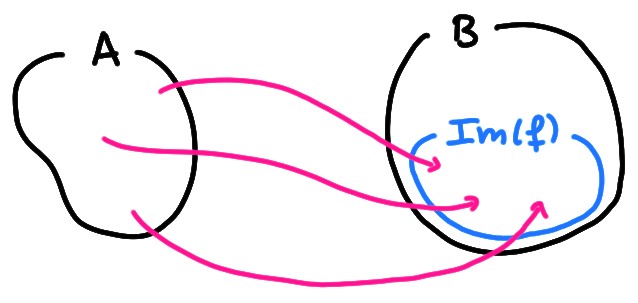
Par la définition de fonction, une flèche sort de chaque \(x\in A\); mais tous les \(y\in B\) ne sont pas forcément atteints par une flèche. L'ensemble image est donc constitué des éléments de l'ensemble d'arrivée qui sont atteints par au moins une flèche. On peut imaginer \(\mathrm{Im} (f)\) obtenu en ''balayant'' tout \(A\) avec la variable \(x\), et en observant tous les \(y=f(x)\in B\) obtenus.
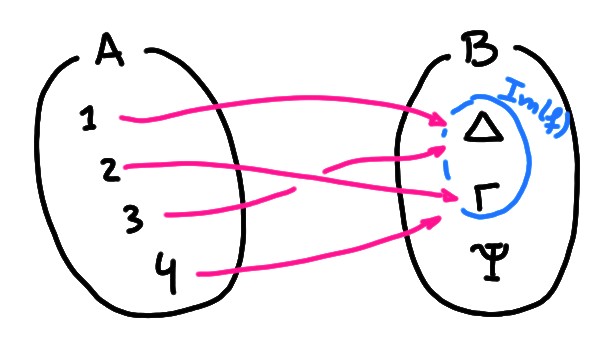
Exemple: Soit \(A=\{1,2,3,4\}\), \(B=\{\Delta, \Gamma, \Psi\}\), et \(f:A\to B\) la fonction définie par: \[ f(1)=\Delta\,,\quad f(2)=\Gamma\,, \quad f(3)=\Delta\,,\quad f(4)=\Gamma\,. \] Alors \(\mathrm{Im} (f)=\{\Delta,\Gamma\}\) (puisque \(\Psi\) n'a pas de préimage).
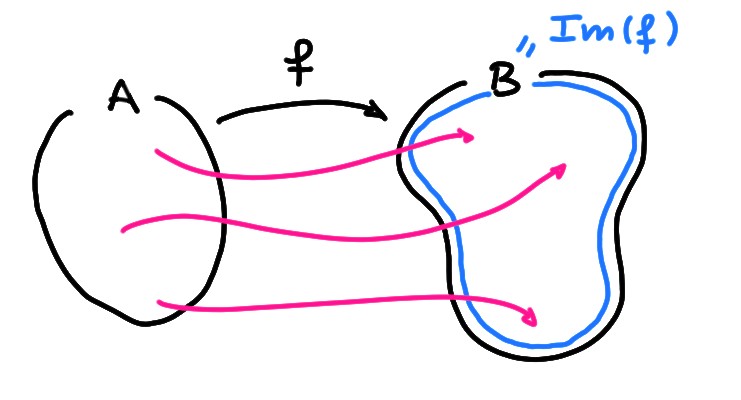
Par définition, l'ensemble image d'une fonction \(f:A\to B\) est un sous-ensemble de \(B\), \(\mathrm{Im} (f)\subset B\), et il est naturel de considérer les fonctions pour lesquelles il coïncide exactement avec \(B\):
Exemple: La fonction \[\begin{aligned} f:\mathbb{Z}&\to \mathbb{Z}\\ x&\mapsto f(x)=x+1 \end{aligned}\] est surjective. En effet, prenons un \(y\in\mathbb{Z}\) quelconque. Si on considère \(x:= y-1\), alors \[f(x)=x+1=(y-1)+1=y\,,\] donc \(x\) est antécédent de \(y\), et donc \(y\in \mathrm{Im} (f)\).
Exemple: Soit \(A\) l'ensemble des étudiant.e.s dans l'auditoire, et soit \(B=\mathbb{N}=\{0,1,2,3,\dots\}\). Considérons \[\begin{aligned} f:A&\to B\\ x&\mapsto f(x)\,, \end{aligned}\] où \(f(x)\) est le nombre de frères et soeurs de \(x\). Pour trouver \(\mathrm{Im} (f)\), on peut procéder comme suit: pour tout \(y\in B\), on pose la question: ''Qui possède exactement \(y\) frères et soeurs?'' Si au moins une main se lève, c'est que \(y\in \mathrm{Im} (f)\). Dès qu'on a un \(y\) pour lequel aucune main se lève, c'est que \(f\) n'est pas surjective. Pour s'assurer facilement que \(f\) n'est effectivement pas surjective, on peut simplement poser la question: ''Est-ce que quelqu'un a plus de \(100\) frères et soeurs?'' Si personne ne lève la main, c'est que \(\mathrm{Im} (f)\subset\{0,1,2,3,\dots,99,100\}\). (Si on sonde l'auditoire, on observe probablement quelque chose comme \(\mathrm{Im} (f)=\{0,1,2,3,4,5\}\).)
Toute fonction peut être transformée en une fonction surjective, en modifiant simplement son ensemble d'arrivée. En effet, si \[\begin{aligned} f:A&\to B\\ x&\mapsto f(x) \end{aligned}\] n'est pas surjective, c'est que son ensemble d'arrivée \(B\) est ''trop grand'': \(\mathrm{Im} (f)\) est un sous-ensemble stricte de \(B\). On peut alors retirer les éléments de \(B\) qui ne sont pas dans l'image, et obtenir une fonction surjective. Plus précisément, \[\begin{aligned} \tilde{f}:A&\to \mathrm{Im} (f)\\ x&\mapsto f(x) \end{aligned}\] est surjective.
Exemple: La fonction \[\begin{aligned} f:\mathbb{N}&\to \mathbb{N}\\ x&\mapsto 2x \end{aligned}\] n'est pas surjective, puisque si \(y\in\mathbb{N}\) est impair, il ne possède pas de préimage. Ici, \(\mathrm{Im} (f)=\mathbb{N}_{\text{pairs}}\), l'ensemble de tous les entiers positifs pairs. En restreignant son ensemble d'arrivée à \(\mathrm{Im} (f)\), on obtient \[\begin{aligned} \tilde{f}:\mathbb{N}&\to \mathbb{N}_{\text{pairs}}\\ x&\mapsto 2x\,, \end{aligned}\] qui est surjective.
Une deuxième chose naturelle à considérer, pour une fonction donnée, est de savoir si celle-ci sépare les points, c'est-à-dire si des points différents, dans l'ensemble de départ, ont des images différentes:
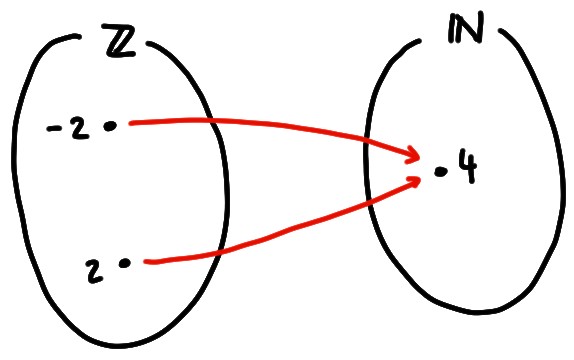
Exemple: Considérons \[\begin{aligned} f:\mathbb{Z}&\to \mathbb{N}\\ x&\mapsto x^2\,. \end{aligned}\] Puisque \(f(-2)=4\) et \(f(2)=4\), \(f\) n'est pas injective.
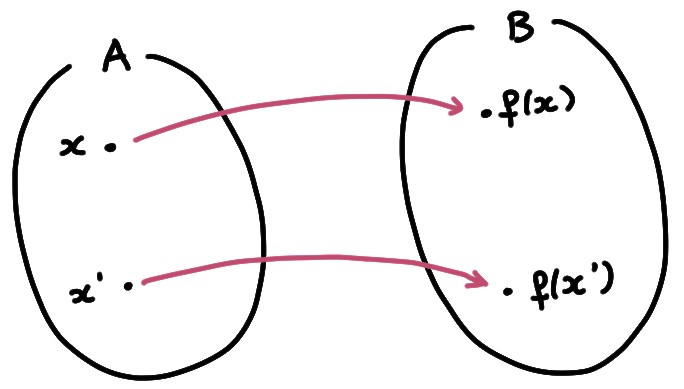
Une caractérisation équivalente de l'injectivité, plus commode à manipuler dans la pratique, est la suivante: \(f\) est injective si \(f(x)=f(x')\) implique \(x=x'\).
Exemple: Montrons que \[\begin{aligned} f:\mathbb{N}&\to \mathbb{Q}\\ x&\mapsto \frac{x^2}{x^2+1} \end{aligned}\] est injective. Pour ce faire, prenons deux éléments \(x,x'\in\mathbb{N}\), et supposons que \(f(x)=f(x')\), c'est-à-dire \[ \frac{x^2}{x^2+1}= \frac{{x'}^2}{{x'}^2+1}\,. \] Quelques manipulations montrent que cette dernière identité est équivalente à \[ x^2-{x'}^2=0\quad \Leftrightarrow \quad (x-x')(x+x')=0\,, \] qui n'est vérifiée que si au moins une des parenthèses est nulle. Or la première est nulle si \(x=x'\), et puisque \(x,x'\in\mathbb{N}\), la deuxième ne peut s'annuler que si \(x=x'=0\). Dans tous les cas, on a bien montré que \(f(x)=f(x')\) implique \(x=x'\), donc \(f\) est injective.
Voyons ce qui se passe lorsqu'une fonction possède en même temps les deux propriétés introduites dans les sections précédentes.
L'intérêt d'une fonction bijective est qu'on peut
l'inverser, ce qui signifie revenir de l'ensemble
image à l'ensemble de départ, sans ambiguïté.
En effet, supposons que \(f:A\to B\) est bijective, et fixons
un élément quelconque de l'ensemble d'arrivée, \(y\in B\).
On en déduit que \(y\) possède exactement une préimage dans l'ensemble de départ: on la note \(f^{-1}(y)\). Avoir associé à tout \(y\in B\) un unique élément \(f^{-1}(y)\in A\) signifie que nous avons défini une fonction de \(B\) dans \(A\). Puisque cette fonction permet d'obtenir l'unique préimage de chaque élément de \(B\), on l'appelle la réciproque de \(f\): \[\begin{aligned} f^{-1}:B&\to A\\ y&\mapsto f^{-1}(y) \end{aligned}\] Par définition, la réciproque permet de récupérer la préimage: \[ f^{-1}(f(x))=x\,\qquad \forall x\in A\,. \] Mais aussi, \[ f(f^{-1}(y))=y\,\qquad \forall y\in B\,. \]
Remarque: L'utilisation du symbole ''\(f^{-1}\)'', pour la réciproque, est largement répandue, et nous l'utiliserons, mais elle peut prêter à confusion. En effet, pour des fonctions numériques, \(f^{-1}(y)\) ne doit en aucun cas être confondu avec \(f(y)^{-1}\), qui signifie \(\frac{1}{f(y)}\)!
Exemple:
Montrons que la fonction \[\begin{aligned} f:{\color{blue}\mathbb{Q}}&\to{\color{magenta}\mathbb{Q}}\\ x&\mapsto f(x)=\frac{x-5}{3} \end{aligned}\] est bijective. (On utilise des couleurs uniquement pour distinguer les ensembles de départ et d'arrivée.)
Maintenant que \(f\) est bijective, donnons sa réciproque explicitement: \[\begin{aligned} f^{-1}:{\color{magenta}\mathbb{Q}}&\to{\color{blue}\mathbb{Q}}\\ y&\mapsto f^{-1}(y)\,. \end{aligned}\] L'expression de \(f^{-1}(y)\) a en fait été trouvée plus haut: il s'agit d'isoler \(x\) dans \(y=f(x)\), ce qui donne \(x=f^{-1}(y)=3y+5\).
Dernière compilation: 2024-01-22 (20:49:36)
Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)
