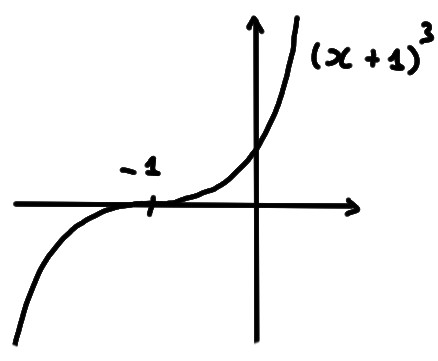Exercice 00-19
Esquisser à la main (sans l'aide d'une calculatrice) les graphes suivants.
- \(y=x^3\)
- \(y=(x+1)^3\)
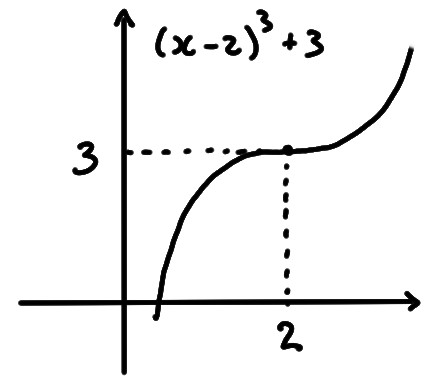
- \(y=(x-2)^3+3\)
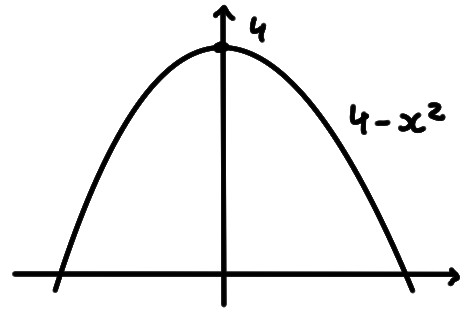
- \(y=4-x^2\)
- \(y=\sqrt{x}\)
- \(y=2\sqrt{x}\)
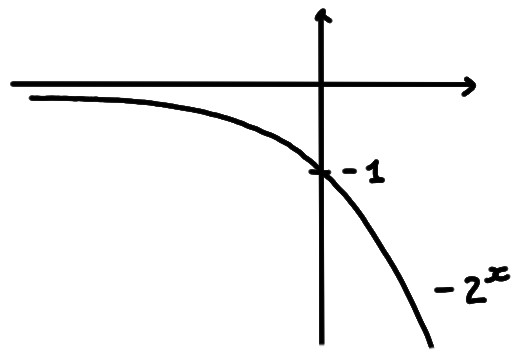
- \(y=-2^x\)
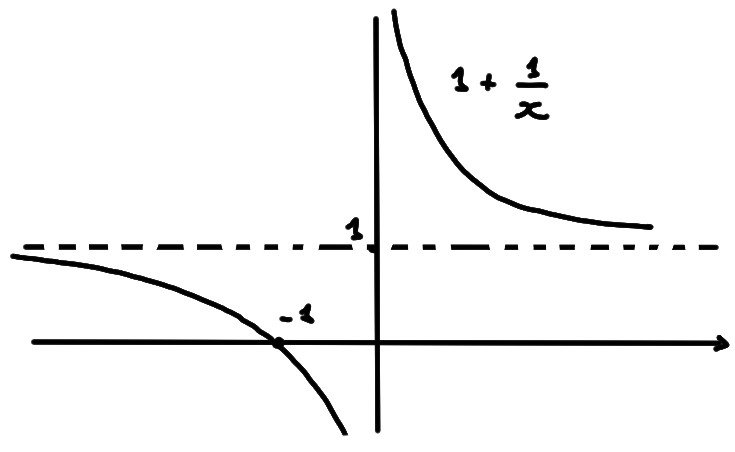
- \(y=1+x^{-1}\)
Il est essentiel de connaître les graphes des fonctions élémentaires
(puissances, trigos, exponentielles et logarithmes), ainsi que des fonctions
obtenus à partir de celles-ci par des transformations élémentaires.
-
-
Ce graphe est celui du dessus, translaté de \(1\) unité vers la gauche:
-
Ce graphe est obtenu à partir de
celui de \(x^2\), translaté de \(2\) unités vers la droite, puis
translaté de \(3\) unités vers le haut:
-
Ce graphe est obtenu à partir de celui de \(x^2\), que l'on commence par
réfléchir à travers l'axe \(Ox\), et qu'on translate ensuite de \(4\) unités
vers le haut:
-
\(\sqrt{x}\) étant la réciproque de \(x^2\), son graphe s'obtient en
réfléchissant celui de \(x^2\) à travers la diagonale
(voir ici, bas de
page):
-
Ce graphe s'obtient à partir de celui de \(\sqrt{x}\), par une dilatation
verticale d'un facteur \(2\):
-
Ce graphe s'obtient à partir de celui de \(2^x\)
(voir ici), par
une réflexion à travers l'axe \(Ox\):
-
Ce graphe s'obtient à partir de celui de \(1/x\)
(voir ici),
par une translation verticale de \(1\) unité vers le haut: