7.7 Limites infinies en un point

Si aucune des limites \[ \lim_{x\to x_0}f(x)\,,\qquad \lim_{x\to x_0^-}f(x)\,,\qquad \lim_{x\to x_0^+}f(x) \] n'existe au sens des définitions précédentes (c'est-à-dire que \(f(x)\) tend vers un \(L\in \mathbb{R}\) bien défini), alors un des scénarios possibles est que les valeurs de \(f(x)\) deviennent arbitrairement grandes à l'approche de \(x_0\), avec un signe bien défini.

Soit \(f\) définie dans un voisinage de \(x_0\).

Limite infinie lorsque \({x\to x_0}\): Limite infinie lorsque \({x\to x_0^+}\): Limite infinie lorsque \({x\to x_0^-}\):

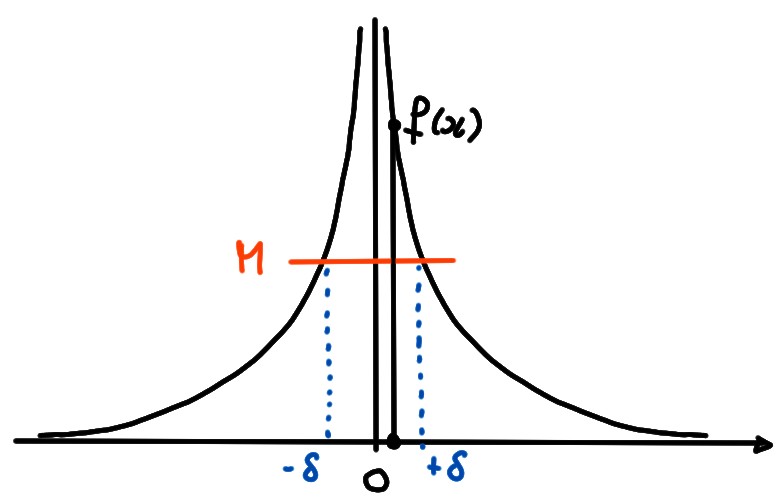
Exemple: Soit \(f(x)=\frac{1}{x^2}\), au voisinage de \(x=0\). Montrons que \[\lim_{x\to 0}f(x)=+\infty\,,\] au sens de la définition ci-dessus. En effet, fixons un seuil \(M\gt 0\), et montrons que \(f(x)\geqslant M\) pour tout \(x\) suffisamment proche de \(0\).

On remarque que pour un \(M\gt 0\) fixé (grand), \[ f(x)\geqslant M\quad \Leftrightarrow \quad \frac{1}{x^2}\geqslant M\quad \Leftrightarrow \quad x^2\leqslant \frac{1}{M}\quad \Leftrightarrow \quad |x|\leqslant \frac{1}{\sqrt{M}}\,. \] Définissons donc \(\delta:= \frac{1}{\sqrt{M}}\). Comme conséquence de ce qui précède, en prenant un \(x\) tel que \(0\lt |x|\leqslant \delta\), on garantit que \(f(x)\geqslant M\).

Exemple: Considérons ensuite \(f(x)=\frac1x\) au voisinage de \(x=0\). Dans ce cas on peut obtenir des limites infinies seulement au sens latéral: \[ \lim_{x\to 0^+}\frac{1}{x}=+\infty\,,\qquad \lim_{x\to 0^-}\frac{1}{x}=-\infty\,. \]

Exemple: Pour \(f(x)=\log_a(x)\), dont le domaine est \(\mathbb{R}_+^*\), \[\lim_{x\to 0^+}\log_a(x)= \begin{cases} -\infty&\text{ si } a\gt 1\,,\\ +\infty&\text{ si }0\lt a\lt 1\,. \end{cases} \]

Propriétés des limites infinies en un point

Comme on sait depuis le chapitre sur les suites, les limites infinies ne se manipulent pas comme leurs analogues finies.

La résultat suivant est l'exact analogue de la proposition donnée pour les suites qui tendent vers l'infini. On ne les formule que dans le cas de la limite \(x\to x_0\). On laisse au lecteur le soin de formuler les propriétés analogues pour les limites latérales \(x\to x_0^\pm\).

Soient \(f,g\) définies dans un voisinage épointé de \(x_0\), et où \(f\) est telle que \(\lim_{x\to x_0}f(x)=+\infty\). Alors
  1. \(\lim_{x\to x_0}\frac{1}{f(x)}=0\).
  2. Si \(\lim_{x\to x_0}g(x)=+\infty\), alors \[\lim_{x\to x_0}(f(x)+g(x))=+\infty\,,\quad \text{et} \quad \lim_{x\to x_0}f(x)g(x)=+\infty\,.\]
  3. Si \(g\) est bornée dans un voisinage épointé de \(x_0\), alors \[ \lim_{x\to x_0}(f(x)+g(x))=+\infty\,,\quad \text{et} \quad \lim_{x\to x_0}\frac{g(x)}{f(x)}=0\,. \]
  4. Si \(\lim_{x\to x_0}g(x)=L\neq 0\), alors \[ \lim_{x\to x_0}f(x)g(x)= \begin{cases} +\infty&\text{ si }L>0,\\ -\infty&\text{ si }L<0\,. \end{cases} \]
  5. Si il existe \(\delta>0\) tel que \(g(x)\geqslant \delta\) dans un voisinage épointé de \(x_0\), alors \(\lim_{x\to x_0}f(x)g(x)=+\infty\).
  6. Si \(g(x)\geqslant f(x)\) pour tout \(x\) dans un voisinage épointé de \(x_0\), alors \(\lim_{x\to x_0}g(x)=+\infty\).

Exemple: Parfois, on peut devoir faire une factorisation avant d'utiliser les propriétés ci-dessus: \[\begin{aligned} \lim_{x\to -1^+} \frac{x^2-1}{x^2+2x+1} &= \lim_{x\to -1^+} \frac{(x-1)(x+1)}{(x+1)^2}\\ &= \lim_{x\to -1^+} \underbrace{(x-1)}_{\to -2\neq 0} \underbrace{\frac{1}{x+1}}_{\to +\infty}=-\infty\,. \end{aligned}\]

Quiz 7.7-1 : Vrai ou faux?
  1. Si \(\lim_{x\to x_0^-}f(x)=+\infty\) et \(\lim_{x\to x_0^-}g(x)=-\infty\), alors \(\lim_{x\to x_0^-}f(x)g(x)=-\infty\).
  2. Si \(\lim_{x\to x_0^+}f(x)=+\infty\) et \(\lim_{x\to x_0^+}g(x)=-\infty\), alors \(\lim_{x\to x_0^+}f(x)e^{g(x)}=0\).
  3. Si \(\lim_{x\to\infty}\frac{f(x)}{g(x)}=\frac{a}{b}\), avec \(a\neq 0\) et \(b\neq 0\), alors \(\lim_{x\to\infty}\frac{e^{f(x)}}{e^{g(x)}}=\frac{e^a}{e^b}\).
Quiz 7.7-2 : Soient \(f,g\) deux fonctions définies au voisinage de \(x_0\). Quelles affirmations sont toujours vraies?
  1. Si \(f(x)\leqslant g(x)\) pour tout \(x\lt x_0\) et si \(\lim_{x\to x_0^-}f(x)=+\infty\), alors \(\lim_{x\to x_0^-}g(x)=+\infty\).
  2. Si \(\lim_{x\to x_0}f(x)g(x)=+\infty\), alors au moins une des limites \(\lim_{x\to x_0}f(x)\), \(\lim_{x\to x_0}g(x)\) doit être \(+\infty\).
  3. Si \(\sup_{]x_0,x_0+\delta[}f=+\infty\) pour tout \(\delta\gt 0\) suffisamment petit, alors \(\lim_{x\to x_0^+}f(x)=+\infty\).
  4. Si \(f\) est bornée dans un voisinage de \(x_0\) et si \(\lim_{x\to x_0^+}g(x)=+\infty\), alors \(\lim_{x\to x_0^+}f(x)g(x)=+\infty\).
  5. Si \(f\) est bornée dans un voisinage de \(x_0\) et si \(\lim_{x\to x_0^+}g(x)=0\), alors \(\lim_{x\to x_0^+}f(x)g(x)=0\).
  6. Si \(\lim_{x\to x_0^+}f(x)=+\infty\), alors il existe \(\delta\gt 0\) tel que \(f\) est décroissante sur \(]x_0,x_0+\delta[\).

Dernière compilation: 2024-01-22 (20:49:38)

Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)