Exercice 08-13
Étudier les limites suivantes.
  1. \(\displaystyle \lim_{x\to 2}\frac{\sqrt{6-x}-2}{\sqrt{3-x}-1}\),
  2. \(\displaystyle \lim_{x\to 3}\frac{|x-3|}{x-3}\)
  3. \(\displaystyle \lim_{x\to 2}\frac{5x-6-x^2}{4-x^2}\)
  4. \(\displaystyle \lim_{x\to -2^+}\frac{5x-6-x^2}{4-x^2}\)
  5. \(\displaystyle \lim_{x\to\infty}e^{x^2} \lfloor e^{8\sqrt{x}-x}\rfloor\)
  6. \(\displaystyle \lim_{x\to 0^{\pm}} x\lfloor\tfrac{1}{x}\rfloor\)
  7. \(\displaystyle \lim_{x\to 0^{\pm}}\lfloor x\rfloor\lfloor\tfrac{1}{x}\rfloor\)
Rappelons qu'avant de se lancer dans un calcul compliqué de limite, il faut d'abord regarder un peu ce que la fonction donnée a l'air de faire dans la limite demandée.

Quand on voit une différence de racines...

... et quand on voit deux différences de racines...

Rappelons que \(\lfloor y \rfloor\) représente la valeur entière de \(y\), et que \[ y-1\lt \lfloor y\rfloor \leqslant y\qquad \forall y\in \mathbb{R} \]

  1. La limite est une indétermination de la forme ''\(\frac00\)''. On multiplie et divise par les conjugués: \[\begin{aligned} \frac{\sqrt{6-x}-2}{\sqrt{3-x}-1} &= \frac{\sqrt{6-x}-2}{\sqrt{3-x}-1} \cdot\frac{\sqrt{6-x}+2}{\sqrt{6-x}+2} \cdot\frac{\sqrt{3-x}+1}{\sqrt{3-x}+1}\\ &= \frac{(\sqrt{6-x})^2-2^2}{(\sqrt{3-x})^2-1^2} \cdot\frac{\sqrt{3-x}+1}{\sqrt{6-x}+2}\\ &= \frac{\sqrt{3-x}+1}{\sqrt{6-x}+2} \end{aligned}\] On a donc \[ \lim_{x\to 2} \frac{\sqrt{6-x}-2}{\sqrt{3-x}-1} = \lim_{x\to 2} \frac{\sqrt{3-x}+1}{\sqrt{6-x}+2} =\frac{2}{4}=\frac12\,. \]
  2. Puisque \[|x-3|= \begin{cases} +(x-3)& \text{ si }x\geqslant 3\,,\\ -(x-3)& \text{ si }x\lt 3\,, \end{cases} \] on a \[ \lim_{x\to 3^+}\frac{|x-3|}{x-3} =\lim_{x\to 3^+}\frac{+(x-3)}{x-3} =\lim_{x\to 3^+}+1=+1\,, \] et \[ \lim_{x\to 3^-}\frac{|x-3|}{x-3} =\lim_{x\to 3^-}\frac{-(x-3)}{x-3} =\lim_{x\to 3^+}-1=-1\,. \] Donc, comme les limites latérales sont différentes, la limite \(\lim_{x\to 3}\frac{|x-3|}{x-3}\) n'existe pas.
  3. La limite est indéterminée de la forme ''\(\frac00\)''. Comme on a, pour tout \(x\) différent de \(\pm 2\), \[ \frac{5x-6-x^2}{4-x^2} =\frac{-(x-2)(x-3)}{-(x-2)(x+2)} =\frac{x-3}{x+2}\,, \] on peut calculer \[ \lim_{x\to 2}\frac{5x-6-x^2}{4-x^2}= \lim_{x\to 2}\frac{x-3}{x+2}=-\frac{1}{4}\,. \]
  4. En utilisant à nouveau la factorisation ci-dessus, \[ \lim_{x\to -2^+}\frac{5x-6-x^2}{4-x^2}= \lim_{x\to -2^+}\frac{x-3}{x+2}=-\infty\,. \] En effet, le numérateur tend vers \(-5\) et le dénominateur est positif lorsque \(x>-2\), et tend vers zéro.
  5. Écrivons \[ (8\sqrt{x}-x)= x\bigl(\frac{8}{\sqrt{x}}-1\bigr)\,. \] Dans ce produit, \(x\) tend vers \(+\infty\), et \(\frac{8}{\sqrt{x}}-1\) tend vers \(-1\). Le produit des deux tend donc vers \(-\infty\). Donc \(\lim_{x\to \infty}(8\sqrt{x}-x)\). Ainsi, \[ \lim_{x\to\infty}e^{8\sqrt{x}-x}=0\,. \] Ceci implique en particulier que \(0\lt e^{8\sqrt{x}-x}\lt 1\), et donc que \(\lfloor e^{8\sqrt{x}-x}\rfloor =0\), pour tout \(x\) suffisamment grand. On a donc \(\lim_{x\to\infty}e^{x^2} \lfloor e^{8\sqrt{x}-x}\rfloor=0\).

    Remarque: Ce qui peut perturber, dans cette limite, est que \(e^{x^2}\) tend vers \(+\infty\) bien plus vite que \(e^{8\sqrt{x}-x}\) ne tend vers zéro, donc \[ \lim_{x\to+\infty}e^{x^2}e^{8\sqrt{x}-x}=+\infty\,. \] Pourtant, la présence de la valeur entière implique \[ \lim_{x\to+\infty}e^{x^2}\lfloor e^{8\sqrt{x}-x}\rfloor=0\,. \]

  6. (fait en cours)
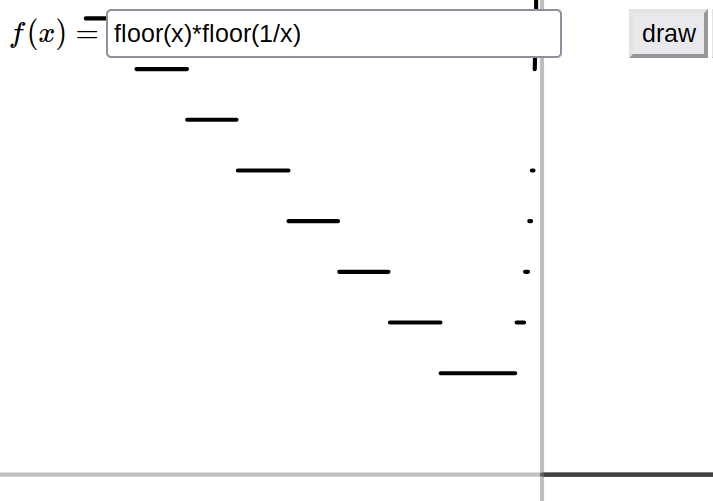
  7. Récrivons la fonction sur l'intervalle \(]-1,1[\). D'abord \[ \lfloor x \rfloor = \begin{cases} -1&\text{ si }-1\lt x\lt 0\,,\\ 0&\text{ si }0\lt x\lt 1\,, \end{cases} \] et ensuite \[\lfloor x\rfloor\lfloor\tfrac{1}{x}\rfloor = \begin{cases} -\lfloor \frac1x \rfloor &\text{ si }-1\lt x \lt 0\,,\\ 0 &\text{ si }0\lt x \lt 1\,, \end{cases} \] donc \[ \lim_{x\to 0^-}\lfloor x\rfloor\lfloor\tfrac{1}{x}\rfloor= -\lim_{x\to 0^-}\lfloor\tfrac{1}{x}\rfloor= +\infty\,, \] et \[ \lim_{x\to 0^+}\lfloor x\rfloor\lfloor\tfrac{1}{x}\rfloor= 0\]