Intuitivement, même si les rationnels sont un sous-ensemble (strict) des réels, ils doivent quand-même être un peu ''partout'' sur la droite des réels, dans le sens où on doit pouvoir en trouver dans n'importe quelle région de la droite, aussi petite soit-elle. On caractérise ceci précisément à l'aide de la notion de densité.
Il est clair que \(\mathbb{R}\) est dense dans lui-même, puisque pour toute paire
\(x,y\in \mathbb{R}\), \(x\lt y\), on peut toujours considérer le point milieu
\(z:= \frac{x+y}{2}\). Donc entre deux réels quelconques distincts, il y a
toujours un autre réel.
Ce qui est plus intéressant, ce sont les ensembles denses dans \(\mathbb{R}\) qui sont
des sous-ensembles stricts de \(\mathbb{R}\), c'est-à-dire qui sont plus petits
que \(\mathbb{R}\).
Théorème: L'ensemble des rationnels \(\mathbb{Q}\) est dense dans \(\mathbb{R}\).
Dans la preuve de ce théorème, nous utiliserons la notion suivante.
Exemple: \[ \lfloor \tfrac{5}{4}\rfloor=1\,,\quad \lfloor -\tfrac{1}{3}\rfloor=-1\,,\quad \lfloor -\sqrt{2}\rfloor=-2\,,\quad \lfloor \pi\rfloor=3\,. \]
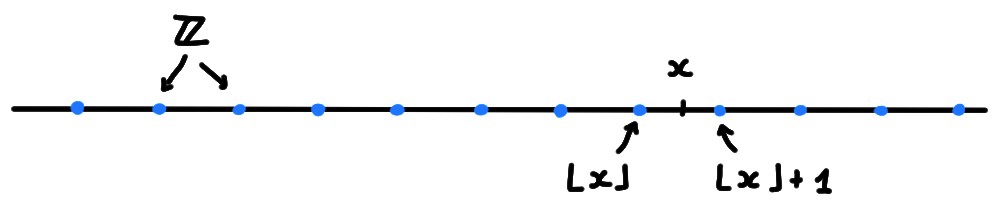
La définition de \(\lfloor x\rfloor\) implique \[\lfloor x\rfloor \leqslant x \lt \lfloor x \rfloor +1\,\qquad \forall x\in \mathbb{R}\,.\] Donc l'image qu'il faut garder en tête est la suivante:
Cette dernière peut aussi s'écrire \[ x-1\lt \lfloor x \rfloor \leqslant x\qquad \forall x\in \mathbb{R}\,. \] Passons à la preuve du théorème.
Soient deux réels \(x\lt y\), et soit \(n\) un entier suffisamment grand, tel que \(n\gt \frac{1}{y-x}\). On rappelle qu'un tel entier existe car \(\mathbb{N}\) n'est pas borné. Posons maintenant \[ r:= \frac{\lfloor nx\rfloor+1}{n}\,. \] Comme c'est un quotient de deux entiers, \(r\) est rationnel. Et puisque \[ nx-1\lt \lfloor nx\rfloor \leqslant nx\,, \] on a \[ \underbrace{\frac{(nx-1)+1}{n}}_{=x}\lt r\leqslant \underbrace{\frac{nx+1}{n}}_{=x+\frac1n\lt y}\,, \] ce qui implique \(x\lt r\lt y\).
La conséquence principale de ce résultat est que l'on peut approximer les réels par des rationnels, dans le sens suivant:
Posons \(x':= x-\varepsilon\), \(y'=x+\varepsilon\). Par le Théorème, il existe un rationnel \(\frac{p}{q}\) tel que \(x'\lt \frac{p}{q}\lt y'\), ce qui implique bien que \(-\varepsilon\leqslant x-\frac{p}{q}\leqslant +\varepsilon\).
En particulier, n'importe quel irrationnel peut être approximé par un rationnel, à un degré arbitraire de précision.
Exemple: Nous avons donné des approximations de \(\pi\) dans l'introduction. Dans le langage de la présente section, ces approximations s'expriment ainsi: \[\begin{aligned} \Bigl|\pi-\frac{22}{7}\Bigr|&\leqslant 0.01 \\ \Bigl|\pi-\frac{333}{106}\Bigr|&\leqslant 0.0001\\ \Bigl|\pi-\frac{103993}{33102}\Bigr|&\leqslant 0.000000001\\ \end{aligned}\] Donc même si \(\pi\) est irrationnel, on sait maintenant qu'on peut fixer un \(\varepsilon>0\) aussi petit que l'on veut, et le théorème garantit qu'il existe un rationnel \(\frac{p}{q}\) à distance au plus \(\varepsilon\) de \(\pi\): \[ \Bigl|\pi-\frac{p}{q}\Bigr|\leqslant \varepsilon\,. \]
Il se trouve que les irrationnels, eux aussi, permettent d'approximer n'importe quel réel:
Théorème: L'ensemble des irrationnels \(\mathbb{R}\setminus\mathbb{Q}\) est dense dans \(\mathbb{R}\).
(exercice)
On utilisera souvent les deux résultats ci-dessus, de la façon suivante: Si \(x\in \mathbb{R}\) est un réel quelconque, alors quel que soit \(\varepsilon\gt 0\) (sous-entendu: aussi petit que l'on veut), il existe toujours un rationnel \(r_*\in\mathbb{Q}\) et un irrationnel \(i_*\in\mathbb{R}\setminus\mathbb{Q}\) tels que \[ r_*\in\left]x-\varepsilon,x+\varepsilon\right[\,,\quad i_*\in\left]x-\varepsilon,x+\varepsilon\right[\,. \]
Dernière compilation: 2024-12-04 (07:30:05)
Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)
