Exercice 13-05
  1. Montrer que \(f\colon [0,1]\to \mathbb{R}\) définie par \[f(x)= \begin{cases} 1&\text{ si }x\in \mathbb{Q}\,,\\ 0&\text{ si }x\in \mathbb{R}\setminus\mathbb{Q}\,, \end{cases} \] n'est pas intégrable.
  2. Montrer que la fonction \(f\colon:[-1,1]\to\mathbb{R}\) définie par \[ f(x)= \begin{cases} 0&\text{ si }x\neq 0\,,\\ C&\text{ si }x= 0\, \end{cases} \] est intégrable, et calculer \(\int_{-1}^1f(x)\,dx\).
On a vu ici que la continuité d'une fonction \(f\colon\left[a,b\right]\to\mathbb{R}\) garantit son intégrabilité. Mais ceci ne signifie pas qu'une fonction qui possède des discontinuités n'est pas intégrable. En particulier, une fonction qui possède des discontinuités isolées est intégrable. La deuxième partie de l'exercice permet de le voir sur un exemple simple.

Si \(\sigma\) est une subdivision de \([0,1]\), on peut remarquer que par la densité de \(\mathbb{Q}\) et \(\mathbb{R}\setminus\mathbb{Q}\) dans \(\mathbb{R}\), chaque intervalle associé à la subdivision \(\sigma\) contient une infinité de rationnels, et une infinité d'irrationnels.

Pour une subdivision \(\sigma\) quelconque de \([-1,1]\),

  1. Soit \(\sigma=(x_0,x_1,\dots,x_n)\) une subdivision de \([0,1]\). Puisque les rationnels sont denses dans \(\mathbb{R}\), chacun des intervalles \(I_k=[x_{k-1},x_k]\) associés à \(\sigma\) contient au moins un rationnel, et donc \[ M_k=\sup_{I_k}f=1\] pour tout \(k\), ce qui implique \[\begin{aligned} \overline{S}_\sigma(f) &=\sum_{k=1}^nM_k(x_k-x_{k-1})\\ &=\sum_{k=1}^n(x_k-x_{k-1})\\ &=x_n-x_0 =1\,. \end{aligned}\] De même, puisque les irrationnels sont denses dans \(\mathbb{R}\), chacun des intervalles \(I_k=[x_{k-1},x_k]\) associés à \(\sigma\) contient au moins un irrationnel, et donc \[ m_k=\inf_{I_k}f=0\] pour tout \(k\), ce qui implique \[ \underline{S}_\sigma(f) =\sum_{k=1}^nm_k(x_k-x_{k-1})=0 \] On a donc \[\begin{aligned} \overline{S}(f)&=\inf_\sigma \overline{S}_\sigma(f)=1\,,\\ \underline{S}(f)&=\sup_\sigma \underline{S}_\sigma(f)=0\,. \end{aligned}\] Ainsi, \(\overline{S}(f)\neq \underline{S}(f)\), et donc \(f\) n'est pas intégrable.
  2. On considère le cas \(C\gt 0\). Soit \(\sigma=(-1,x_1,x_2,\dots,x_{n-1},+1)\) une subdivision de \([-1,1]\). On remarque d'abord que chacun des intervalles \(I_k\) associés à cette subdivision contient au moins un \(x\neq 0\), et donc \[m_k=\inf_{I_k}f=0\] La somme de Darboux inférieure est donc égale à \(\underline{S}_\sigma(f)=0\). Ceci implique en particulier que \[ \underline{S}(f)=\sup_\sigma \underline{S}_\sigma(f)=0\,. \] Pour la somme supérieure associée à \(\sigma\), on considère deux cas:
    • \(\sigma\) ne contient pas le point \(0\): dans ce cas, il existe exactement un intervalle \(I_k=[x_{k-1},x_k]\) contenant \(0\).
      Pour cet intervalle, on a \[ M_k=\sup_{I_k}f=C\,, \] alors que pour tous les autres intervalles ce nombre est zéro. On a donc \[ \overline{S}_\sigma(f)=C(x_k-x_{k-1})\,. \]
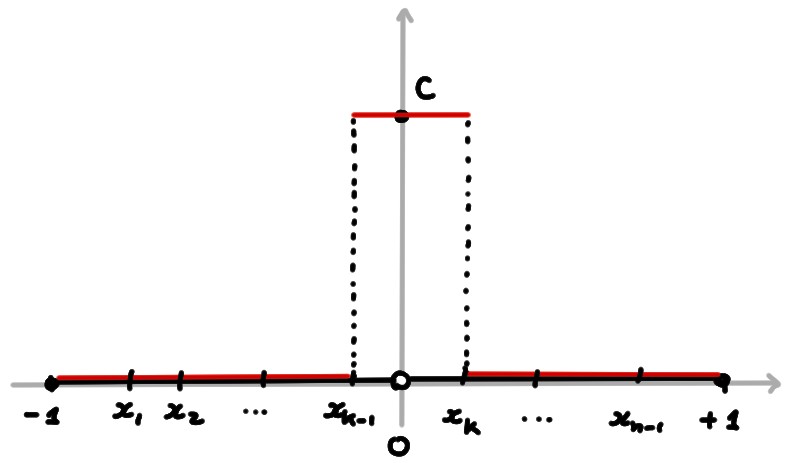
    • \(\sigma\) contient le point \(0\): dans ce cas, il existe exactement deux intervalles de la forme \(I_k=[x_{k-1},0]\), \(I_{k+1}=[0,x_{k+1}]\). Puisque ces intervalles contiennent \(0\), \[ M_k=M_{k+1}=C\,, \] alors que pour tous les autres intervalles ce nombre est zéro. On a donc \[\begin{aligned} \overline{S}_\sigma(f) &=C(0-x_{k-1})+C(x_{k+1}-0)\\ &=C(x_{k+1}-x_{k-1})\,. \end{aligned}\]
    Puisque dans les deux cas, la somme de Darboux supérieure ne dépend que d'une différence entre deux points consécutifs de la subdivision, cette différence peut être rendue aussi petite que nécessaire en prenant une subdivision pour laquelle la distance entre deux points consécutifs \(x_{k-1}\) et \(x_k\) devient arbitrairement petite. Ainsi, \[ \overline{S}(f)=\inf_\sigma \overline{S}_\sigma(f)=0\,. \] On a donc \(\overline{S}(f)=\underline{S}(f)=0\), ce qui signifie que \(f\) est intégrable et que \[ \int_{-1}^{1}f(x)\,dx=0\,. \]