12.3 Les fonctions intégrables

Se pose maintenant la question de savoir quelles fonctions sont réellement intégrables au sens de la définition donnée plus haut.

Commençons par un exemple (trop) simple.

Exemple: Soit \(f:[a,b]\to \mathbb{R}\) une fonction constante: \(f(x)=C\).

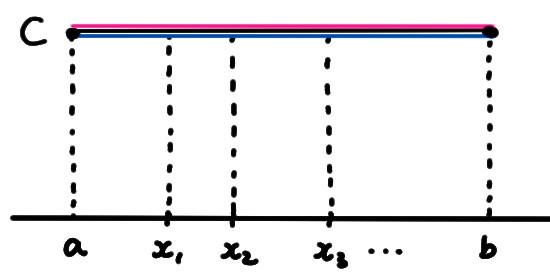
Si \(C>0\), on sait que l'intégrale doit exister, et puisqu'elle représente l'aire du rectangle de base \([a,b]\) et de hauteur \(C\), elle doit être égale à \(C(b-a)\). Voyons pourquoi c'est effectivement le cas.

Soit \(\sigma\) une subdivision de \([a,b]\). Puisque \(m_k=C\) pour tout \(k\), la Darboux inférieure vaut \[\begin{aligned} \underline{S}_\sigma(f) &=\sum_{k=1}^n m_k(x_k-x_{k-1})\\ &=C\sum_{k=1}^n (x_k-x_{k-1})\\ &=C((\cancel{x_1}-x_0)+(\cancel{x_2}-\cancel{x_1})+\dots+(x_n-\cancel{x_{n-1}}))\\ &=C(x_n-x_0)\\ &=C(b-a)\,. \end{aligned}\] De même, \(M_k=C\) pour tout \(k\), et donc la somme de Darboux supérieure vaut \(\overline{S}_\sigma(f)=C(b-a)\). Puisque les sommes ne dépendent pas du choix de la subdivision, ceci implique \[\begin{aligned} \underline{S}(f)&=\sup_\sigma \underline{S}_\sigma(f)=C(b-a)\,,\\ \overline{S}(f)&=\inf_\sigma \overline{S}_\sigma(f)=C(b-a)\,,\\ \end{aligned}\] et donc \(\underline{S}(f)=\overline{S}(f)\), ce qui entraîne que \(f\) est intégrable et que son intégrale vaut \[ \int_a^bf(x)\,dx=C(b-a)\,. \]

Ce dernier exemple est excessivement simple: puisque la fonction est constante, les sommes de Darboux sont constantes et ne dépendent pas de la subdivision, donc ne donnent aucun travail particulier.

Mais en général, dès que la fonction n'est plus constante, les sommes de Darboux sont toujours différentes, \(\underline{S}_\sigma(f)\lt \overline{S}_\sigma(f)\), peu importe la subdivision, et montrer qu'elles peuvent malgré tout être rendues proches l'une de l'autre semble être un problème difficile.

Dans la section suivante, nous allons donner un résultat qui, même s'il ne permet pas forcément de calculer une intégrale, pourra au moins garantir l'intégrabilité...

Remarque: Les résultats énoncés sur cette page sont donnés sans démonstration, puisqu'ils reposent tous, pour la plupart, sur la notion de continuité uniforme, une notion qui n'est pas traitée dans ce cours.

Une condition suffisante pour l'intégrabilité: la continuité

Théorème: Si \(f:[a,b]\to \mathbb{R}\) est continue, alors elle est intégrable.

Par conséquent, toutes les fonctions fondamentales (polynômes, fonctions trigo, exponentielles et logarithmes) sont intégrables sur les intervalles fermés et bornés contenus dans leurs domaines.

En fait, on peut montrer qu'il suffit que \(f\) soit continue par morceaux pour être intégrable:

La résultat ci-dessus a la conséquence suivante: si une fonction n'est pas intégrable, c'est qu'elle doit être ''très discontinue''.

Exemple: Soit \(f:[0,1]\to \mathbb{R}\) définie par \[ f(x):= \begin{cases} 1&\text{ si }x\in \mathbb{Q}\cap[0,1]\,,\\ 0&\text{ si }x\in (\mathbb{R}\setminus\mathbb{Q})\cap[0,1]\,. \end{cases} \] On voit facilement que \(\underline{S}_\sigma(f)=0\) et \(\overline{S}_\sigma(f)=1\), quelle que soit la subdivision \(\sigma\). Donc \(f\) n'est pas intégrable.

Voyons ensuite un résultat qui montre que l'on peut en principe calculer l'intégrale d'une fonction continue en choisissant des suites de subdivisions.

Pour une subdivision \(\sigma=(x_0,x_1,\dots,x_n)\), on définit \[ |\sigma|:=\max_{1\leqslant k\leqslant n}|x_k-x_{k-1}|\,. \]

Théorème: Soit \(f:[a,b]\to \mathbb{R}\) continue, et \(\sigma^{(N)}\) une suite de subdivisions telle que, dans la limite où \(N\to \infty\), \[ |\sigma^{(N)}|\to 0 \,. \] Alors \[ \overline{S}_{\sigma^{(N)}}(f)\to \int_a^bf(x)\,dx\,, \qquad \text{ et } \underline{S}_{\sigma^{(N)}}(f)\to \int_a^bf(x)\,dx\,. \]

Dans la pratique, on utilise souvent une suite de partitions régulières, où \(\sigma^{(N)}\) contient \(N\) intervalles de longueurs égales. Voyons cela sur un exemple.

Exemple: Considérons l'aire sous la ''parabole d'Archimède'', dont l'équation est \[f(x)=1-x^2\,,\qquad x\in [-1,1]\,.\]

Par parité, il suffit de calculer l'aire de la moitié de l'aire sous la courbe, disons la partie de droite: \[ \int_{-1}^{1}f(x)\,dx=2\int_0^1 f(x)\,dx\,. \] \(f\) étant continue, on peut utiliser le théorème et calculer l'intégrale en utilisant une suite de subdivisions Le plus simple, dans ce cas, est d'utiliser des subdivisions régulières. Prenons donc la suite de subdivisions \(\sigma^{(1)}, \sigma^{(2)}, \dots\) définie par \[ \sigma^{(N)}=\bigl( 0,\tfrac{1}{N}, \tfrac{2}{N}, \dots, \tfrac{N-1}{N}, 1 \bigr)\,, \] Dans \(\sigma^{(N)}\), on a que \(x_k-x_{k-1}=\frac{1}{N}\). On peut maintenant récrire précisément la somme de Darboux supérieure: \[\begin{aligned} \overline{S}_{\sigma^{(N)}}(f) &=\sum_{j=0}^{N-1}f(\tfrac{j}{N})\frac{1}{N}\\ &=\frac{1}{N}\sum_{j=0}^{N-1}\Bigl(1-\bigl(\frac{j}{N}\bigr)^2\Bigr)\\ &=1-\frac{1}{N^3}\sum_{j=0}^{N-1}j^2\\ &=1-\frac{(N-1)N(2(N-1)+1)}{6N^3} \end{aligned}\] Dans cette dernière ligne, on a utilisé la formule \[ \boxed{ 1^2+2^2+3^2+4^2+\dots+n^2=\frac{n(n+1)(2n+1)}{6}\,. } \] (Pour une preuve, voir ce qui a été fait ici.)

Donc, par le théorème, \[\begin{aligned} \int_0^1f(x)\,dx &=\lim_{N\to \infty} \overline{S}_{\sigma^{(N)}}(f)\\ &=1-\lim_{N\to \infty}\frac{(N-1)N(2(N-1)+1)}{6N^3}\\ &=1-\frac26=\frac23\,, \end{aligned}\] ce qui implique \[ \int_{-1}^1f(x)\,dx=\frac43=1.33333\dots\,. \]

Propriétés des fonctions intégrables
Soient \(f,g:[a,b]\to \mathbb{R}\) intégrables.
  1. Linéarité: pour toutes constantes \(\lambda_1,\lambda_2\in\mathbb{R}\), \[ \int_a^b\bigl(\lambda_1f(x)+\lambda_2g(x)\bigr)dx = \lambda_1\int_a^bf(x)dx+ \lambda_2\int_a^bg(x)dx\,. \]
  2. Pour tout \(a\lt c\lt b\), on a la relation de Chasles \[ \int_a^bf(x)dx= \int_a^cf(x)dx+ \int_c^bf(x)dx\,. \]
  3. Si \(f(x)\leqslant g(x)\) pour tout \(x\in [a,b]\), alors \[ \int_a^bf(x)dx\leqslant \int_a^bg(x)dx\,. \]
  4. Si \(\alpha\leqslant f(x)\leqslant \beta\) pour tout \(x\in [a,b]\), alors \[\alpha(b-a)\leqslant \int_a^b f(x)\,dx\leqslant \beta(b-a)\,.\]
  5. \[\Bigl|\int_a^b f(x)\,dx\Bigr|\leqslant \int_a^b|f(x)|\,dx\,.\]

La relation de Chasles est valable seulement lorsque \(a\lt c\lt b\), mais pour qu'elle reste vraie plus généralement, \[ \int_a^bf(x)\,dx + \int_b^af(x)\,dx = \int_a^af(x)\,dx=0\,, \] nous adopterons la convention suivante: \[ \boxed{ \int_b^af(x)\,dx:= -\int_a^bf(x)\,dx\,. } \]

Quiz 12.3-1 : Soit \(f:[a,b]\to \mathbb{R}\). Vrai ou faux?
  1. Si \(f\) est bornée, alors \(f\) est intégrable.
  2. Si \(f\) n'est pas bornée, alors \(f\) n'est pas intégrable.
  3. Si \(f\) est continue, alors \(f\) est intégrable.
  4. Si \(f\) n'est pas continue en au moins un point \(x_0\in ]a,b[\), alors \(f\) n'est pas intégrable.
  5. Si \(f\) est intégrable, alors \(f\) est continue.
  6. Si \(f\) est intégrable, alors \(f\) est continue par morceaux.
  7. Si \(f\) est dérivable sur \(]a,b[\), alors \(f\) est intégrable.
  8. Si \(f\) est intégrable, alors pour tout \(a\lt c\lt d\lt b\), \(f:[c,d]\to\mathbb{R}\) est aussi intégrable.
Quiz 12.3-2 : Soit \(f:[a,b]\to \mathbb{R}\) une fonction bornée, intégrable. Vrai ou faux?
  1. \(\int_a^bf(x)\,dx\) représente l'aire sous le graphe de \(f\).
  2. Si \(\int_a^bf(x)\,dx\geqslant 0\), alors \(f(x)\geqslant 0\) pour tout \(x\in [a,b]\).
  3. Si \(\int_a^bf(x)\,dx\geqslant 0\), alors l'intégrale représente l'aire sous le graphe de \(f\).
  4. Si \(f(x)=C\) pour tout \(x\in [a,b]\), alors \(\int_a^bf(x)\,dx=C(b-a)\).
  5. Si \(f(x)\geqslant 0\) pour tout \(x\in [a,b]\), alors \(\int_a^bf(x)\,dx\geqslant 0\).
Quiz 12.3-3 : Soit \(f:\mathbb{R}\to\mathbb{R}\) une fonction continue et périodique, de période \(T\). Vrai ou faux?
  1. \(\int_{-T}^Tf(x)\,dx=0\)
  2. \(\int_{-T}^0f(x)\,dx=\int_0^T f(x)\,dx\)
  3. \(\int_{0}^{nT}f(x)\,dx=n\int_0^T f(x)\,dx\) (\(n\in \mathbb{N}\))
  4. La limite \(\lim_{n\to\infty}\frac{1}{n}\int_{-n}^{n}f(x)\,dx\) existe

Dernière compilation: 2024-10-05 (22:34:29)

Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)