Exercice 14-14
  1. Montrer que pout tout \(n\geqslant 2\), \[ \log(n+1)\leqslant \sum_{k=1}^n \frac{1}{k}\leqslant \log(n)+1 \]
  2. Calculer la limite \[ \lim_{n\to\infty}\frac{1+ \frac{1}{2}+\frac13+\cdots+\frac1n}{\log(n)} \]
  3. Estimer l'entier \(N\) à partir duquel la somme partielle de la série harmonique, \(s_n\), dépasse le seuil \(M=50\).
On pourra s'inspirer des comparaisons entre sommes et intégrales, vues ici.

Interpréter la somme avec une somme d'aire de rectangles, puis comparer cette somme avec des parties de l'aire sous la courbe \(\frac{1}{t}\).

  1. Considérons la somme \(\sum_{k=1}^n\frac{1}{k}\). On interprète chaque terme \(\frac{1}{k}\) comme l'aire d'un rectangle dont un coin supérieur est sur le graphe de la fonction \(f(x)=\frac1x\). Pour commencer, interprétons \(\frac1k\) comme l'aire du rectangle rouge situé à droite du point \(x=k\), de hauteur \(\frac1k\):
    Dans ce cas, la somme des aires des rectangles rouges (\(k=1,\dots,n\)) est plus grande que l'aire sous le graphe de \(f(x)=\frac1x\), entre \(x=1\) et \(x=n+1\): \[ \sum_{k=1}^{n}\frac1k\geqslant \int_1^{n+1}\frac{1}{x}\,dx =\log(n+1)-\log(1)=\log(n+1)\,. \] Ensuite, interprétons \(\frac1k\) comme l'aire du rectangle bleu situé à gauche du point \(x=k\), de hauteur \(\frac1k\):
    Dans ce cas, la somme des aires des rectangles bleus (\(k=2,\dots,n\)) est plus petite que l'aire sous le graphe de \(f(x)=\frac1x\), entre \(x=1\) et \(x=n\): \[\begin{aligned} \sum_{k=1}^{n}\frac1k =\frac11+\sum_{k=2}^{n}\frac1k &\leqslant 1+ \int_1^{n}\frac{1}{x}\,dx\\ &=1+\log(n)-\log(1)=\log(n)+1\,. \end{aligned}\]
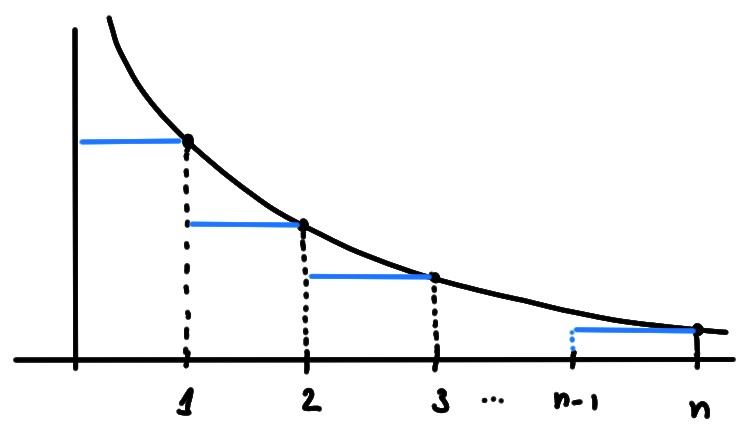
  2. De la première partie, on a que \[ \underbrace{\frac{\log(n+1)}{\log(n)}}_{=1+\frac{\log(1+\frac1n)}{\log(n)}} \leqslant \frac{\sum_{k=1}^n\frac{1}{k}}{\log(n)} \leqslant 1+\frac{1}{\log(n)}\,. \] Par le théorème des deux gendarmes, \[ \lim_{n\to\infty} \frac{\sum_{k=1}^n\frac{1}{k}}{\log(n)}=1\,. \]
  3. Si \(s_n=1+\frac12+\dots+\frac1n\), on sait que on sait depuis longtemps que \(s_n\to+\infty\), mais cela devient maintenant transparent puisque la première partie de l'exercice a montré que \[ \log(n+1)\leqslant s_n\leqslant \log(n)+1\,. \] Mais le minorant permet maintenant de montrer que si on veut garantir que \(s_n\geqslant 50\), alors il suffit d'imposer que \(\log(n+1)\geqslant 50\), qui est équivalente à \(n\geqslant e^{50}-1\). Ce nombre est de l'ordre de \(5\cdot 10^{21}\).