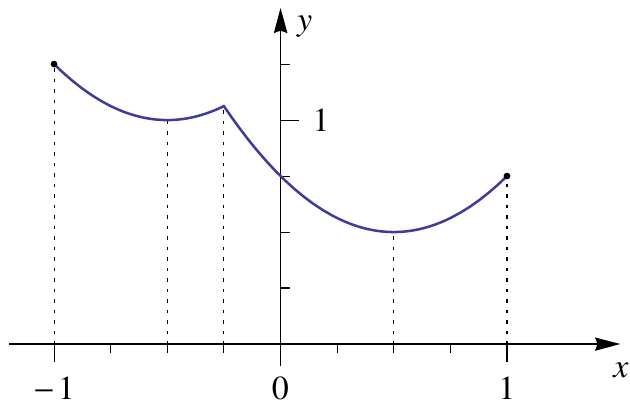
Trouver et charactériser
les extremas locaux et l'ensemble image de la fonction
\(f:[-1,1]\to \mathbb{R}\) définie par
\[
f(x)=x^{2}-\left|x+\tfrac{1}{4}\right|+1\,.
\]
Remarquons que \(f\) étant continue sur un intervalle fermé et borné, elle
atteint ses extrema globaux.
On les trouve en implémentant l'algorithme vu au cours.
Récrivons \(f\) en distinguant les deux cas. On a
\[\begin{aligned}
f(x)&=\begin{cases}
x^2+x+\frac{5}{4}\,, & -1\leqslant x\leqslant -\frac{1}{4} \\
x^2-x+\frac{3}{4}\,, & -\frac{1}{4}\lt x\leqslant 1
\end{cases}\,,\\
f'(x)&=\begin{cases}
2x+1\,, & -1\lt x\lt -\frac{1}{4} \\
2x-1\,, & -\frac{1}{4}\lt x\lt 1
\end{cases}
\end{aligned}\]
En \(x_0=-\frac{1}{4}\),
\[\begin{aligned}
f'_+(x_0) &= \lim\limits_{x\to {x_0}^+}\dfrac{f(x)-f(x_0)}{x-x_0}\\
&=\lim\limits_{x\to -\frac{1}{4}^+}\frac{x^2-x-\frac{5}{16}}{x+\frac{1}{4}}\\
&=\lim\limits_{x\to -\frac{1}{4}^+}
\frac{\left(x-\frac{5}{4}\right)\left(x+\frac{1}{4}\right)}{x+\frac{1}{4}}=-\frac{3}{2}
\end{aligned}\]
\[\begin{aligned}
f'_-(x_0) &= \lim\limits_{x\to {x_0}^-}\dfrac{f(x)-f(x_0)}{x-x_0}\\
&= \lim\limits_{x\to -\frac{1}{4}^-} \frac{x^2+x+\frac{3}{16}}{x+\frac{1}{4}}\\
& =
\lim\limits_{x\to -\frac{1}{4}^-}
\frac{\left(x+\frac{3}{4}\right)\left(x+\frac{1}{4}\right)}{x+\frac{1}{4}}\\
&=\frac{1}{2}
\end{aligned}\]
et donc \(f\) n'est pas dérivable en ce point: c'est un point stationnaire.
Remarque:
On aurait aussi pu calculer ces dérivées latérales à l'aide d'un résultat
au cours (Conséquence 3):
comme \(f\) est continue en \(x_0\), les limites
\[
\lim_{x\to x_0^+}f'(x)\,,\qquad
\lim_{x\to x_0^-}f'(x)\,,
\]
si elles existent, donnent les dérivées latérales en \(x_0\).
Les extrema locaux et absolus sont donc parmi les points suivants:
- \(f'(x)=0\), ce qui a lien en \(x_1=-\frac{1}{2}\) et
\(x_2=\frac{1}{2}\).
Comme \(f''(x_1)=f''(x_2)\gt 0\), \(x_1\)
et \(x_2\) sont des minima locaux.
On a \(\boxed{f(x_1)=1}\) et \(\boxed{f(x_2)=\frac{1}{2}}\).
- Points où \(f'\) n'existe pas: Le seul point à examiner est
\(x_0=-\frac{1}{4}\) pour lequel on a vu que
\(f'_+(x_0) = -\frac{3}{2}\) et
\(f'_-(x_0) = \frac{1}{2}\,\) (voir ci-dessus).
En ce point, \(f(x_0) = \frac{17}{16}\).
- Bord du domaine de \(f\):
\(\boxed{f(-1)=\frac{5}{4}}\) et \(\boxed{f(1)=\frac{3}{4}}\).
Donc on peut conclure:
- \(f\) possède un maximum global en \(x=-1\), où \(f(-1)=\frac{5}{4}\)
- \(f\) possède un minimum global en \(x=\frac{1}{2}\), où
\(f(\frac{1}{2})=\frac{1}{2}\).
On en déduit que \(\mathrm{Im} (f)=[\frac12,\frac54]\).