Analyse 1 | S. Friedli (EPFL)

9.12 Sur la recherche des extrema d'une fonction sur un intervalle $[a,b]$

Passons maintenant à l'utilisation de la dérivée dans la recherche des extrema d'une fonction.

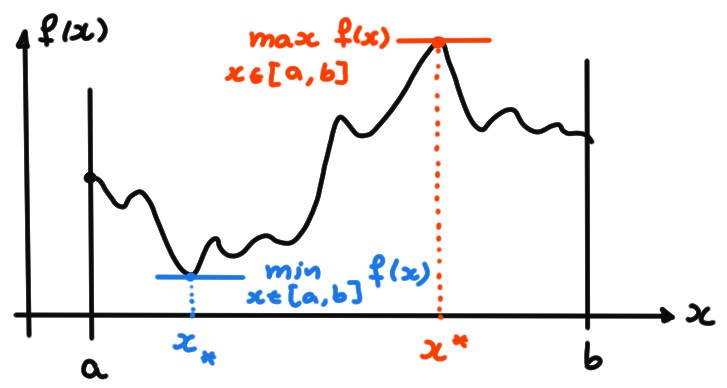
On sait que lorsque $f:[a,b]\to \mathbb{R}$ est continue, elle atteint son minimum et son maximum:

Dans cette section, on décrit un algorithme qui permet (en principe) de trouver ces extrema par le calcul.

Considérons, pour fixer les idées, la recherche du maximum global d'une fonction $f:[a,b]\to \mathbb{R}$ . On supposera que $f$ est continue. Par simple observation, puisqu'on sait qu'il est atteint quelque part sur $[a,b]$ , on peut facilement lister toutes les possibilités:

Il peut être atteint sur les bords, en $x=a$ ou en $x=b$ .
Il peut être atteint à l'intérieur de l'intervalle, c.-à-d. dans $]a,b[$ . Mais comme c'est un maximum global, il est aussi local. Donc si $f$ est dérivable en ce point, sa dérivée s'y annule. Et si elle n'est pas dérivable, on traite le cas séparément.

Cette simple distinction des cas nous mène directement à un algorithme pour la recherche du minimum et du maximum de $f$ :

On commencera par chercher les points stationnaires, c'est-à-dire les points $x\in ]a,b[$ où $f$ est dérivable et s'annule: $f'(x)=0$ , ainsi que les points de $]a,b[$ où $f$ n'est pas dérivable.
On regardera les valeurs de la fonction sur le bord de l'intervalle, en $x=a$ et $x=b$ , et on les comparera avec les valeurs en chacun des points trouvés à l'étape précédente.
Après avoir listé toutes ces valeurs, on garde la plus grande, et la plus petite.

Remarque: On a vu (dans Continuité sur un intervalle compact) que si $f:[a,b]\to\mathbb{R}$ est continue, alors son ensemble image est un intervalle fermé et borné, donné par $\mathrm{Im} (f)= \bigl[ \min_{x\in [a,b]}f(x)\,,\,\max_{x\in [a,b]}f(x) \bigr]\,,$ et peut donc être trouvé à l'aide de l'algorithme décrit ci-dessus.

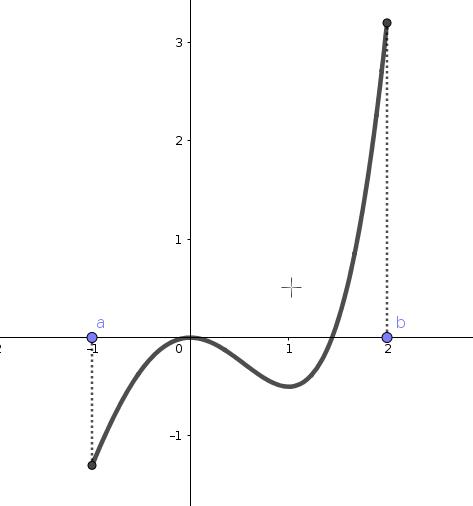
Exemple: Cherchons les extremas de la fonction $f(x)=3x^4+4x^3-12x^2$ sur $[-1,2]$ .

Points stationnaires: $\begin{aligned} f'(x)=12(x^3+x^2-2x)&=12x(x^2+x-2)\\ &=12x(x+2)(x-1)\,, \end{aligned}$ donc la dérivée est nulle en $-2\not \in [-1,2]$ , en $0\in [-1,2]$ et en $1\in [-1,2]$ . On garde: $\boxed{f(0)=0\,\quad f(1)=-5}$
Sur les bords: $\boxed{f(-1)=-13,\,\quad f(2)=32}$

En comparant les quatre valeurs encadrées ci-dessus, on voit que

$f$ atteint son maximum global en $x=2$ (sur le bord)
$f$ atteint son minimum global en $x=-1$ (sur le bord)

En particulier,

\mathrm{Im} (f)=[-13,32]\,.

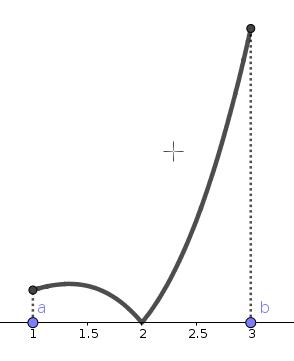
Exemple: Considérons $f(x)=|x^2(x-2)|$ sur l'intervalle $[1,3]$ . Comme $f:[1,3]\to \mathbb{R}$ est continue, elle atteint son minimum et son maximum. On commence par écrire $|x^2(x-2)|= \begin{cases} -x^2(x-2)&\text{ si }x\in [1,2]\,,\\ x^2(x-2)&\text{ si }x\in ]2,3]\,. \end{cases}$

Points stationnaires: Sur $]1,2[$ , $f'(x)=x(4-3x)$ , donc deux points où la dérivée s'annule, en $0\not \in ]1,2[$ et en $\frac43\in]1,2[$ : $\boxed{f(\tfrac43)=\frac{32}{27}}$ Sur $]2,3[$ , $f'(x)=x(3x-4)$ , donc ne s'annule pas.
Points où $f$ n'est pas dérivable? Seul candidat: $x=2$ . En effet, $\begin{aligned} \lim_{x\to 2^-}f'(x)&=\lim_{x\to 2^-}(x(4-3x))=-4\\ \lim_{x\to 2^+}f'(x)&=\lim_{x\to 2^+}(x(3x-4))=+4 \end{aligned}$ Donc on garde $\boxed{f(2)=0}$
Sur les bords: $\boxed{f(1)=1\,\quad f(3)=9}$

On conclut que

f

atteint son minimum en $x=2$ ,
atteint son maximum en $x=3$ (sur le bord).

Remarquons qu'en

x=\frac43

,

f

possède un maximum, qui est local mais pas global.

On a aussi montré que

\mathrm{Im} (f)=[0,9]

Quiz 9.12-1 : Soit

f:[a,b]\to \mathbb{R}

continue. Vrai ou faux?

Si $x_0\in ]a,b[$ est un point stationnaire de $f$ , alors $x_0$ est soit un minimum local, soit un maximum local.
Le nombre de points stationnaires de $f$ dans $]a,b[$ est fini.
Si $f$ possède une infinité de points stationnaires dans $]a,b[$ , alors $f$ atteint son maximum en une infinité de points.
Si $f$ possède dans $]a,b[$ plus de points stationnaires que de points où elle n'est pas dérivable, alors elle atteint son minimum et son maximum en un point stationnaire.