- VRAI. Soient \(x_1,x_2 \in \mathbb{R}\) tels que \(x_1 \lt x_2\). Si \(f\) est strictement croissante, on a \(f(x_1) \lt f(x_2)\) et si \(f\) est strictement décroissante, on a \(f(x_1)\gt f(x_2)\). Dans les deux cas \(f(x_1)\neq f(x_2)\), c.-à-d. que \(f\) est injective.
- FAUX.
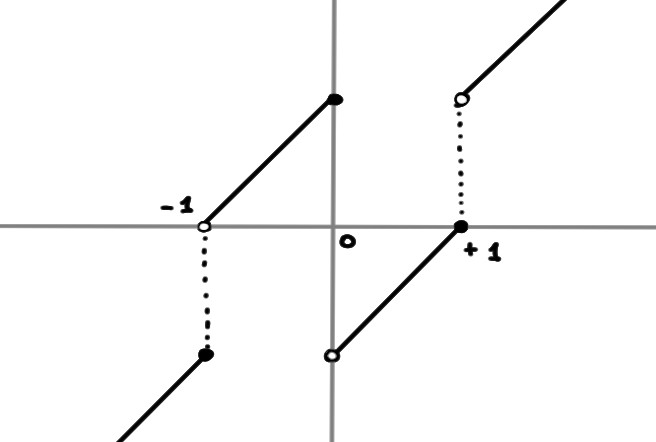
Par exemple, la fonction suivante est injective mais pas monotone:
\[
f(x):=
\begin{cases}
x&\text{ si }x\leqslant -1\\
x+1&\text{ si }-1\lt x\leqslant 0\\
x-1&\text{ si }0\lt x\leqslant 1\\
x&\text{ si }x\gt1\\
\end{cases}
\]
- FAUX. Prendre par exemple \(f(x)=x\), qui est croissante, pour laquelle \(f^{-1}(x)=x\), qui est aussi croissante.
- FAUX. Prendre par exemple \(f(x)=x\) et \(g(x)=-x\). Alors \((f\circ g)(x)=-x\) est décroissante mais \(f\) ne l'est pas.