Pour chaque fonction \(f\) définie sur l'intervalle \(I\),
trouver le domaine de définition de la fonction réciproque \(f^{-1}\) et esquisser
les graphes de \(f\) et \(f^{-1}\).
Rem.: Tous les domaines \(I\) sont
choisis en sorte que la fonction réciproque existe.
- \( f(x)=\sin(x)\) sur
\(I=\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\)
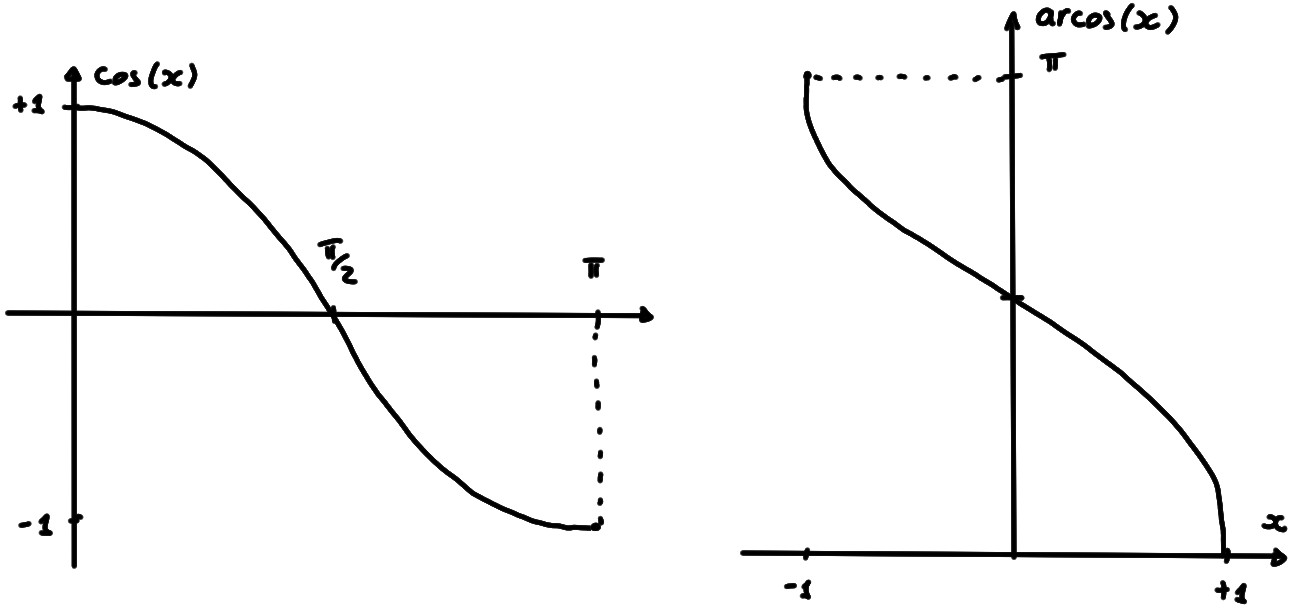
- \( f(x)=\cos(x)\) sur \(I=[0,\pi]\)
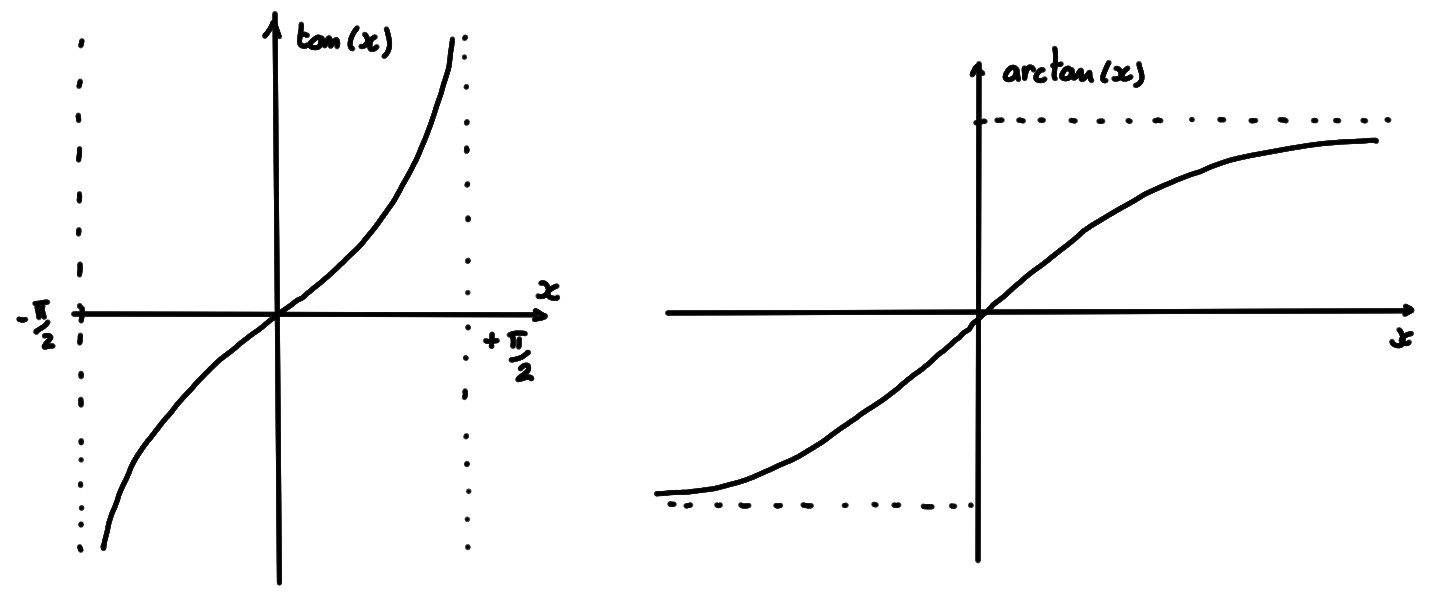
- \( f(x)=\tan(x)\) sur
\(I=\left] -\frac{\pi}{2},\frac{\pi}{2}\right[\)
- \( f(x)=e^x\) sur \(I=\mathbb{R}\)
Cet exercice consiste uniquement à tester la compréhension des fonctions
réciproques des fonctions trigonométriques
(voir
ici)
et exponentielles
(voir
ici).
Notons que le
domaine \(D(f^{-1})\) de la fonction réciproque \(f^{-1}\) est l'image de
\(f\). En effet, dans chacun des cas,
\(I\) a été choisi pour que \(f\) soit injective et surjective, et
donc \(f\) est bijective entre \(I\) et son image.
Rappelons aussi que le graphe de
\(f^{-1}\) s'obtient en faisant une réflexion de celui de \(f\)
par rapport à la droite \(y=x\).
-
\[\begin{aligned}
\arcsin: [-1,1]&\to [-\frac{\pi}{2},\frac{\pi}{2}]\\
x&\mapsto \arcsin(x)
\end{aligned}\]
-
\[\begin{aligned}
\arccos: [-1,1]&\to [0,\pi]\\
x&\mapsto \arccos(x)
\end{aligned}\]
-
\[\begin{aligned}
\arctan: \mathbb{R}&\to [-1,1]\\
x&\mapsto \arctan(x)
\end{aligned}\]
-
\[\begin{aligned}
\log: ]0,+\infty[&\to \mathbb{R}\\
x&\mapsto \log(x)
\end{aligned}\]
