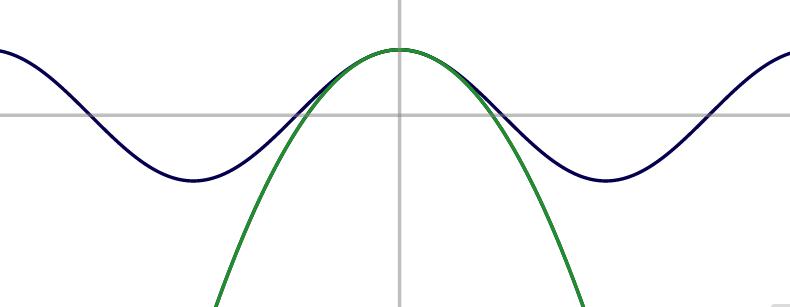
Montrer l'inégalité suivante: pour tout
\(x\in\mathbb{R}\),
\[
\cos(x)\geqslant 1-\frac{x^2}{2}\,.
\]
On a vu
ici (dans Conséquence 1)
comment utiliser le Théorème des Accroissements finis pour
obtenir l'
inégalité universelle
\[
e^x\geqslant 1+x\qquad \forall x\in \mathbb{R}\,.
\]
Pour commencer
On posera \(f(x):=\cos(x)-1+\frac{1}{2}x^2\). Comme \(f\) est paire, on
essaiera de montrer que
\[ f(x)\geqslant 0 \qquad \forall x\geqslant 0
\]
...
Mais puisque \(f(0)=0\), il s'agit en fait de montrer que
\[ f(x)\geqslant f(0) \qquad \forall x\geqslant 0
\]
Et pour ce faire, il est suffisant de montrer que \(f\) est croissante sur
\([0,+\infty[\).
Soit \(f(x):=\cos(x)-1+\frac{1}{2}x^2\).
Puisque \(f\) est paire, il suffit de montrer que
\(f(x)\geqslant 0\) pour \(x\geqslant 0\).
On a
\[f(0)=\cos(0)-1+0=0\,, \]
donc le résultat suivra du théorème des accroissements finis
si on peut montrer que
que \(f'(x)\geqslant 0\) pour tout \(x>0\). Or
\[ f'(x) = -\sin(x)+x\,. \]
Deux façons de montrer que cette dernière est \(\geqslant 0\):
- Comme \(\sin(x)\leqslant x\) pour tout \(x\geqslant 0\), on a
\[
f'(x)=-\sin(x)+x\geqslant -\sin(x)+\sin(x)=0\,.
\]
-
Mais on a \(f'(0)=0\). De nouveau, par
un résultat vu au cours,
il suffit de montrer que \(f''(x)\geqslant 0\) pour \(x\gt 0\).
Or,
\[
f''(x)=-\cos(x)+1\geqslant 0\,,
\]
parce que \(\cos(x)\in[-1,1]\).