Analyse 1 | S. Friedli (EPFL)

9.13 Dérivée seconde et convexité/concavité

Fonctions convexes/concaves

Rappelons qu'une fonction \(f\) est convexe si pour toute paire de points \(x_1\lt x_2\), et pour tout \(\lambda\in[0,1]\), \[ f((1-\lambda)x_1+\lambda x_2)\leqslant (1-\lambda) f(x_1)+\lambda f(x_2)\,.\] L'interprétation géométrique étant la suivante: si on choisit deux points quelconques sur le graphe de \(f\), le segment qui les relie est entièrement au-dessus du graphe.

Or on peut remarquer que lorsque \(f\) est dérivable, c'est-à-dire lorsque \(f'(x)\) est défini pour tout \(x\), alors la convexité semble être équivalente à la croissance de \(x\mapsto f'(x)\):

Sur l'animation ci-dessus, on a une fonction qui est manifestement convexe et dérivable, et on observe que sa dérivée est croissante. Ceci implique que si la dérivée est dérivable, et si la dérivée de la dérivée, c'est-à-dire la dérivée seconde, est positive, alors la fonction doit être convexe. Plus précisément:

Théorème: Soit \(I\) un intervalle ouvert, \(f:I\to \mathbb{R}\) deux fois dérivable sur \(I\) (\(f\) est dérivable, et \(f'\) est aussi dérivable sur \(I\)).

Si \(f''(x)\geqslant 0\) pour tout \(x\in I\), alors \(f\) est convexe sur \(I\).
Si \(f''(x)\leqslant 0\) pour tout \(x\in I\), alors \(f\) est concave sur \(I\).

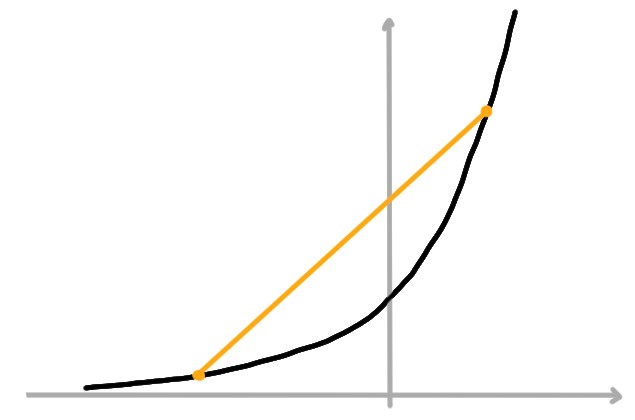
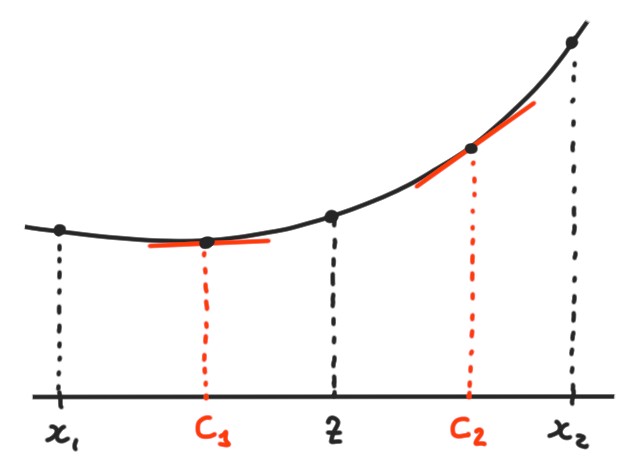
Il suffit de démontrer la première implication. Remarquons d'abord que comme \(f''\geqslant 0\), \(f'\) est croissante sur \(I\). Soient \(x_1\lt x_2\) dans \(I\). Fixons \(\lambda \in ]0,1[\) et posons \(z:= (1-\lambda)x_1+\lambda x_2\).

On applique deux fois le théorème des accroissements finis:

Sur \([x_1,z]\): il existe \(c_1\in]x_1,z[\) tel que \[ f'(c_1)=\frac{f(z)-f(x_1)}{z-x_1} \]
Sur \([z,x_2]\): il existe \(c_2\in]z,x_2[\) tel que \[ f'(c_2)=\frac{f(x_2)-f(z)}{x_2-z} \]

Remarquons que comme \(c_1\lt c_2\), et puisque \(f'\) est croissante, \[ f'(c_1)\leqslant f'(c_2) \] Donc \[\begin{aligned} f(z)-f(x_1)&\leqslant f'(c_2)(z-x_1) \qquad |\cdot(1-\lambda)\\ f(x_2)-f(z)&=f'(c_2)(x_2-z) \qquad |\cdot\lambda \end{aligned}\] En soustrayant les deux inégalités (multipliées par \(1-\lambda\) et \(\lambda\)), on trouve \[\begin{aligned} f(z)-&\bigl\{ (1-\lambda)f(x_1)+\lambda f(x_2) \bigr\}\leqslant\\ &f'(c_2)\bigl( \underbrace{(1-\lambda)(z-x_1)-\lambda(x_2-z)}_{=0}\bigr)=0\,. \end{aligned}\] On a donc montré que \[ f(z) \leqslant (1-\lambda)f(x_1)+\lambda f(x_2)\,. \]

Exemple: Prenons \(f(x)=x^2\) sur \(\mathbb{R}\). Comme \[f''(x)=2\gt 0\qquad \forall x\in \mathbb{R}\,,\] le théorème garantit que \(f\) est convexe.

Exemple: Prenons \(f(x)=e^x\) sur \(\mathbb{R}\). Puisque \[f''(x)=e^x\gt 0\qquad \forall x\in \mathbb{R}\,,\] le théorème garantit que \(f\) est convexe.

Exemple: Considérons maintenant \(f(x)=\log(x)\), sur \(\mathbb{R}_+^*\). Comme \[ f''(x)=-\frac{1}{x^2}\lt 0\qquad \forall x\in \mathbb{R}_+^*\,, \] le théorème entraîne que \(f\) est concave:

Exemple: Considérons le polynôme \(f(x)=x^4-x^2\), et cherchons les intervalles sur lesquels \(f\) est convexe/concave. Puisque \(f\) est deux fois dérivable, l'étude du signe de \(f''(x)=2(6x^2-1)\) donne:

On en déduit par le théorème que:

\(f\) est convexe sur \(]-\infty,-\sqrt{1/6}[\),
\(f\) est concave sur \(]-\sqrt{1/6},+\sqrt{1/6}[\),
\(f\) est convexe sur \(]+\sqrt{1/6},+\infty[\).

Les points \(P_\pm=(\pm\sqrt{1/6},f(\pm \sqrt{1/6}))\) sont des points d'inflexion: ce sont des points du graphe où la nature de la courbe change, passant de concave (resp. convexe) à convexe (resp. concave).

Quiz 9.13-1 : Soit \(I\) un intervalle ouvert et borné, \(f:I\to \mathbb{R}\). Vrai ou faux?

Si \(f\) n'est pas deux fois dérivable, alors elle n'est pas convexe.
Si \(f\) n'est pas dérivable, alors elle n'est pas convexe.
Si \(f\) est deux fois dérivable sur \(I\) et si \(f''(x)=0\) pour tout \(x\in I\), alors \(f\) est convexe.
Si \(f\) est convexe, alors elle est majorée.

Quiz 9.13-2 : Soit \(f:\mathbb{R}\to \mathbb{R}\) convexe. Vrai ou faux?

\(f\) atteint son minimum.
Il n'existe aucun intervalle \([a,b]\) sur lequel \(f\) est de la forme \(f(x)=mx+h\).
Si \(\displaystyle\lim_{x\to-\infty}f(x)= \lim_{x\to+\infty}f(x)=+\infty\), alors il existe \(\beta\in \mathbb{R}\) tel que \(f\) est décroissante sur \(]-\infty,\beta]\), croissante sur \([\beta,+\infty[\).
Si \(f\) est bornée, alors c'est une constante.
\(f\) est continue ⚡.