Rappelons qu'une fonction est continûment dérivable si elle est dérivable et que sa dérivée est continue. Voir les détails ici.

Toutes les fonctions \(f:\mathbb{R}\to\mathbb{R}\) données ici sont définies sur \(\mathbb{R}\): \(D(f)=\mathbb{R}\). On pourra donc, pour chacune: , on pourra donc

1. Commencer par étudier \(f'\), ainsi que son domaine \(D(f')\).
2. Étudier les points de \(D(f')\) en lesquels \(f'\) est continue.

Pour 3. et 4.

1. Remarquons que \(f\) est dérivable en tout \(x\neq 1\) (puisque c'est un quotient bien défini de fonctions dérivables), mais que \[\lim_{x\to 1}f(x)=1\neq 0=f(1)\,,\] et donc \(f\) n'est pas continue en \(1\), donc elle n'est pas non plus dérivable en \(1\). Donc \(D(f')=\mathbb{R}\setminus\{1\}\). Ensuite, comme \[ f'(x)=\frac{(x-1)\cos(x-1)-\sin(x-1)}{(x-1)^2} \qquad \forall x\neq 1\,, \] \(f'\) est clairement continue sur \(\mathbb{R}\setminus\{1\}\). Donc \(f\) est continûment dérivable sur \(\mathbb{R}\setminus\{1\}\), mais pas dérivable en \(1\).
2. Pour \(x\neq 0\), \(f\) est un produit de fonctions dérivables, elle est donc dérivable et \[\begin{aligned} f'(x) &= \sin(x)\sin(\tfrac{1}{x})+x\cos(x)\sin(\tfrac{1}{x}) - x\sin(x)\cos(\tfrac{1}{x})\tfrac{1}{x^{2}}\\ &= \sin(x)\sin(\tfrac{1}{x})+x\cos(x)\sin(\tfrac{1}{x}) - \tfrac{1}{x}\sin(x)\cos(\tfrac{1}{x})\,. \end{aligned}\] Pour la dérivée de \(f\) en \(x=0\), on a \[\begin{aligned} f'(0) & =\lim_{x\to 0}\frac{f(x)-f(0)}{x-0}\\ &=\lim_{x\to 0}\frac{x\sin(x)\sin(\tfrac{1}{x})-0}{x} \\ &=\lim_{x\to 0}(\sin(x)\sin(\tfrac{1}{x}))\\ &= \lim_{x\to 0}\frac{\sin(x)}{x} \,\lim_{x\to 0}(x\sin(\tfrac{1}{x}))\\ &=0\,, \end{aligned}\] où on a utilisé: \[ \lim_{x\to 0}\frac{\sin(x)}{x}= 1 \qquad \text{et} \qquad \lim_{x\to 0}x\sin(\tfrac{1}{x}) = 0\,. \] \(f\) est donc dérivable partout, \(D(f')=\mathbb{R}\), et sa dérivée est donnée par \[ f'(x)= \begin{cases} \sin(x)\sin(\frac{1}{x})+x\cos(x)\sin(\frac{1}{x}) - \frac{1}{x}\sin(x)\cos(\frac{1}{x})&\text{ si }x\neq 0\\ 0&\text{ si }x=0\,. \end{cases} \] Il est donc clair que \(f'\) est continue en tout \(x_0\neq 0\), puisqu'en ces points c'est une somme de produits de composées de fonctions dérivables.
   Pour la continuité de \(f'\) en \(x_0=0\), il faut voir si \(\lim_{x\to 0}f'(x)\) existe et vaut \(f'(0)=0\). Pour le premier terme, on a déjà vu ci-dessus que \[ \lim_{x\to 0}(\sin(x)\sin(\frac{1}{x}))=0\,. \] Pour le deuxième terme de \(f'\) on a \[ \lim_{x\to 0}x\cos(x)\sin(\tfrac{1}{x}) = \lim_{x\to 0}\cos(x) \,\cdot\, \lim\limits_{x\to 0}(x\sin(\tfrac{1}{x}))=1\cdot 0=0\,. \] Pour le troisième terme \[ -\frac{1}{x}\sin(x)\cos(\frac{1}{x}) =-\frac{\sin(x)}{x}\cos(\frac{1}{x})\,, \] on a bien-sûr existence de la limite de \(\frac{\sin (x)}{x}\), par contre \(\cos(\frac1x)\) n'a pas de limite lorsque \(x\to 0\). On en conclut que \(f'(x)\) n'a pas de limite lorsque \(x\to 0\), donc \(f'\) n'est pas continue en \(x=0\), ce qui implique que \(f\not\in C^1(\mathbb{R})\).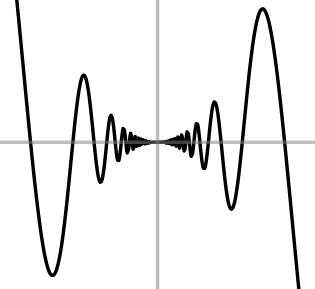
   
3. On a, pour tout \(x\neq 0\), \(f'(x)=\arctan(\frac{1}{x})-\frac{x}{1+x^2}\), qui est continue sur \(\mathbb{R}^*\). Par contre, \[ f'_{\pm}(0) =\lim_{x\to 0^\pm} \frac{f(x)-f(0)}{x-0} =\lim_{x\to 0^\pm} \arctan(\tfrac{1}{x})=\pm\frac{\pi}{2}\,. \] Donc \(f\) n'est pas dérivable en \(x=0\). Ainsi, \(D(f')=\mathbb{R}^*\).
4. On a, pour tout \(x\neq 0\), \(f'(x)=2x\arctan(\frac{1}{x})-\frac{x^2}{1+x^2}\), qui est continue sur \(\mathbb{R}^*\). Ensuite, \[ f'(0) =\lim_{x\to 0} \frac{f(x)-f(0)}{x-0} =\lim_{x\to 0} x\arctan(\tfrac{1}{x})=0\,, \] (puisque \(\arctan\) est bornée sur \(\mathbb{R}\)) et donc \(f\) est dérivable en \(0\). De plus, comme \[ \lim_{x\to 0}f'(x) =\lim_{x\to 0}\Bigl\{ 2x\arctan(\frac{1}{x})-\frac{x^2}{1+x^2} \Bigr\} =0=f'(0)\,, \] et donc \(f'\) est continue aussi en \(x=0\). Ainsi, \(f\in C^1(\mathbb{R})\).