Rappelons que le graphe de la fonction réciproque \(f^{-1}\) est le réfléchi du graphe de \(f\) à travers la diagonale:
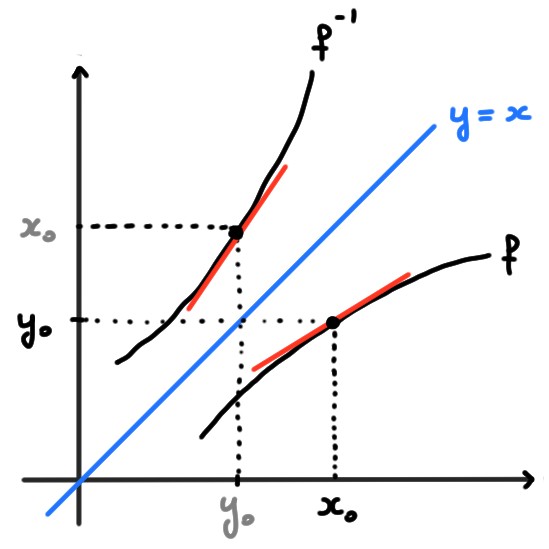
Rappelons que le graphe de la fonction réciproque \(f^{-1}\) est le réfléchi du graphe de \(f\) à travers la diagonale:
Or la réflexion d'une droite de pente \(m\neq 0\) à travers la diagonale est une droite de pente \(\frac{1}{m}\). On s'attend donc à ce que la dérivée de \(f^{-1}\) au point \((y_0,x_0)\) soit égale à l'inverse de la dérivée de \(f\) au point \((x_0,y_0)\):
Théorème: Soit \(I=\left]a,b\right[\) un intervalle ouvert, et \(f:I\to F\) une fonction bijective (en particulier, \(F=\mathrm{Im} (f)\)), dont la réciproque est notée \(f^{-1}:F\to I\). Soit encore \(x_0\in I\). Si \(f\) est dérivable en \(x_0\) et si \(f'(x_0)\neq 0\), alors \(f^{-1}\) est dérivable en \(y_0=f(x_0)\), et \[ (f^{-1})'(y_0)=\frac{1}{f'(x_0)}=\frac{1}{f'(f^{-1}(y_0))}\,. \]
Pour étudier la dérivée de la réciproque \(f^{-1}\) au point \(y_0=f(x_0)\), on
considère le quotient
est \[
\frac{f^{-1}(y)-f^{-1}(y_0)}{y-y_0}\,.
\]
Comme \(f\) est bijective, on peut associer à tout \(y\) proche de \(y_0\)
son unique préimage, \(x=f^{-1}(y)\).
Clairement, \(y\to y_0\) implique \(x\to x_0\).
On peut donc récrire la limite
\[\begin{aligned}
\frac{f^{-1}(y)-f^{-1}(y_0)}{y-y_0}
= \frac{1}{\frac{y-y_0}{f^{-1}(y)-f^{-1}(y_0)}}
= \frac{1}{ \frac{f(x)-f(x_0)}{x-x_0} }\,.
\end{aligned}\]
Puisque \(f'(x_0)\neq 0\), le
dénominateur de cette dernière fraction est non nul dès que \(x\) est
suffisamment proche de \(x_0\), c'est-à-dire lorsque \(y\) est suffisamment
proche de \(y_0\).
Maintenant, en prenant la limite,
\[\begin{aligned}
\lim_{y\to y_0}
\frac{f^{-1}(y)-f^{-1}(y_0)}{y-y_0}
&=
\lim_{x\to x_0}
\frac{1}{ \frac{f(x)-f(x_0)}{x-x_0} }\\
&=\frac{1}{f'(x_0)}\\
&=\frac{1}{f'(f^{-1}(y_0))}\,.
\end{aligned}\]
Exemple: Supposons qu'on connaît \((e^x)'=e^x\) mais qu'on ne sait plus dériver \(\log(x)\). Comme elles sont réciproques l'une de l'autre, que \(f(x)=e^x\) est dérivable partout et que sa dérivée n'est jamais nulle, on a \[ e^{\log(y)}=y\,, \] que l'on dérive par rapport à \(y\), \[ \underbrace{e^{\log (y)}}_{=y}(\log(y))'=1 \] On retrouve alors: \[(\log(y))'=\frac{1}{y}\,.\]
Dérivons maintenant les réciproques des fonctions trigonométriques.
Exemple: Rappelons que la réciproque du sinus est \[\begin{aligned} \arcsin:[-1,1]&\to [-\tfrac{\pi}{2},\tfrac{\pi}{2}]\\ x&\mapsto \arcsin(x) \end{aligned}\] Par définition, \[ y=\sin(\arcsin(y))\qquad\forall y\in [-1,1] \] Puisque la dérivée du sinus ne s'annule nulle part sur \(]-\frac{\pi}{2},\frac{\pi}{2}[\), le théorème garantit que \(\arcsin\) est dérivable sur \(]-1,1[\). En prenant la dérivée par rapport à \(y\) des deux côtés de cette dernière identité: si \(y\in ]-1,1[\), \[ 1=\bigl( \sin(\arcsin(y)) \bigr)'=\cos(\arcsin(y))(\arcsin(y))'\,. \] Comme l'angle \(\arcsin (y)\in ]-\tfrac{\pi}{2},\tfrac{\pi}{2}[\), son cosinus est positif, et donc \[ \cos(\arcsin(y))=\sqrt{1-\sin(\arcsin(y))^2}=\sqrt{1-y^2}\,. \] On a donc \[ \boxed{ (\arcsin(y))'=\frac{1}{\sqrt{1-y^2}}\qquad \forall y\in ]-1,1[ } \]
Exemple: Rappelons que la réciproque du cosinus est \[\begin{aligned} \arccos:[-1,1]&\to [0,\pi]\\ x&\mapsto \arccos(x) \end{aligned}\] Par définition, \[ y=\cos(\arccos(y))\qquad\forall y\in [-1,1] \] Puisque la dérivée du cosinus ne s'annule nulle part sur \(]0,\pi[\), le théorème garantit que \(\arccos\) est dérivable sur \(]-1,1[\). On calcule sa dérivée en prenant la dérivée par rapport à \(y\) des deux côtés de cette dernière identité: si \(y\in ]-1,1[\), \[ 1=\bigl( \cos(\arccos(y)) \bigr)'=-\sin(\arccos(y))(\arccos(y))'\,. \] Comme l'angle \(\arccos (y)\in ]0,\pi[\), son sinus est positif, et donc \[ \sin(\arccos(y))=\sqrt{1-\cos(\arccos(y))^2}=\sqrt{1-y^2}\,. \] On a donc \[ \boxed{ (\arccos(y))'=\frac{-1}{\sqrt{1-y^2}}\qquad \forall y\in ]-1,1[ } \]
Exemple: Rappelons que la réciproque de la tangente est \[\begin{aligned} \arctan:\mathbb{R}&\to ]-\tfrac{\pi}{2},\tfrac{\pi}{2}[\\ x&\mapsto\arctan(x) \end{aligned}\] Par définition, \[ y=\tan(\arctan(y))\qquad\forall y\in \mathbb{R} \] Comme la dérivée de la tangente ne s'annulle nulle part sur \(]-\tfrac{\pi}{2},\tfrac{\pi}{2}[\), \(\arctan\) est dérivable partout sur \(\mathbb{R}\). En dérivant rapport à \(y\) des deux côtés de cette dernière identité, \[\begin{aligned} 1&=\bigl( \tan(\arctan(y)) \bigr)'\\ &=(1+\tan^2(\arctan(y)))(\arctan(y))'\\ &=(1+y^2)(\arctan(y))'\,. \end{aligned}\] On a donc \[ \boxed{(\arctan(y))'=\frac{1}{1+y^2}\qquad \forall y\in \mathbb{R}\,.} \]
Dernière compilation: 2024-10-05 (22:34:29)
Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)
