Exercice 05-07
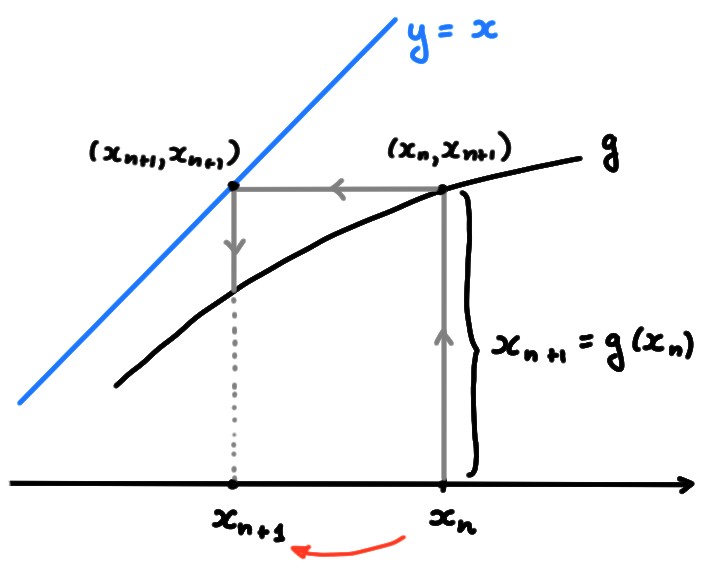
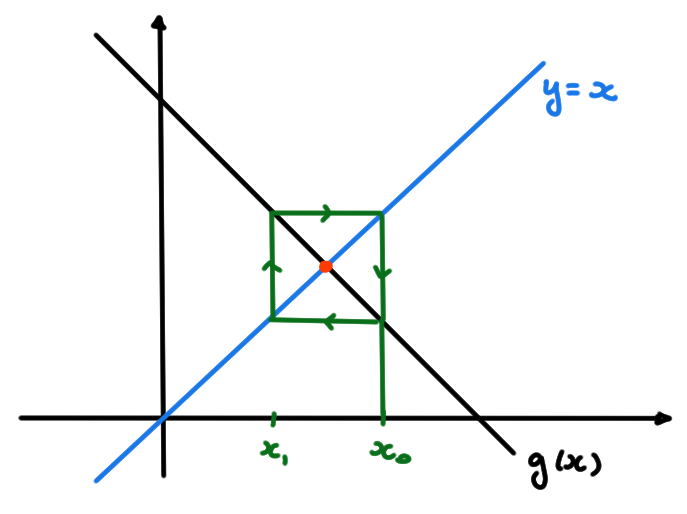
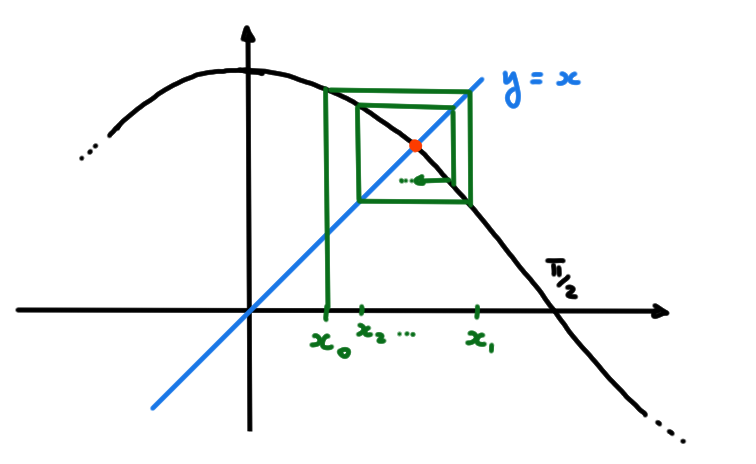
Décrire le comportement des suites \(x_{n+1}=g(x_n)\) ci-dessous dans la limite \(n\to \infty\), qualitativement, uniquement à l'aide de l'interprétation graphique de la trajectoire. On considérera en particulier le comportement en fonction du choix de la condition initiale.
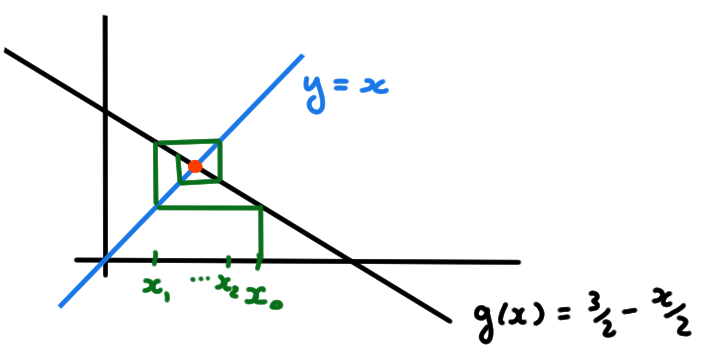
  1. \(x_0\in \mathbb{R}\), \(g(x):= \frac{3-x}{2}\).
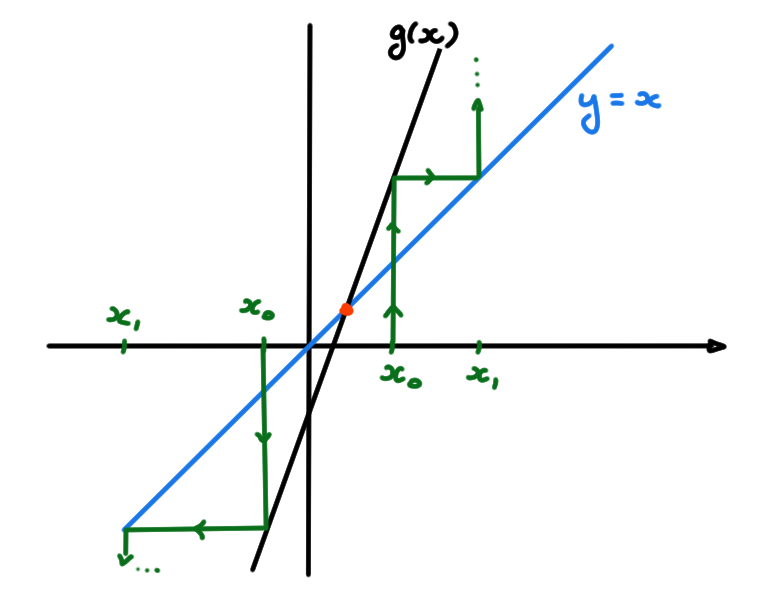
  2. \(x_0\in \mathbb{R}\), \(g(x):= 2x-5\).
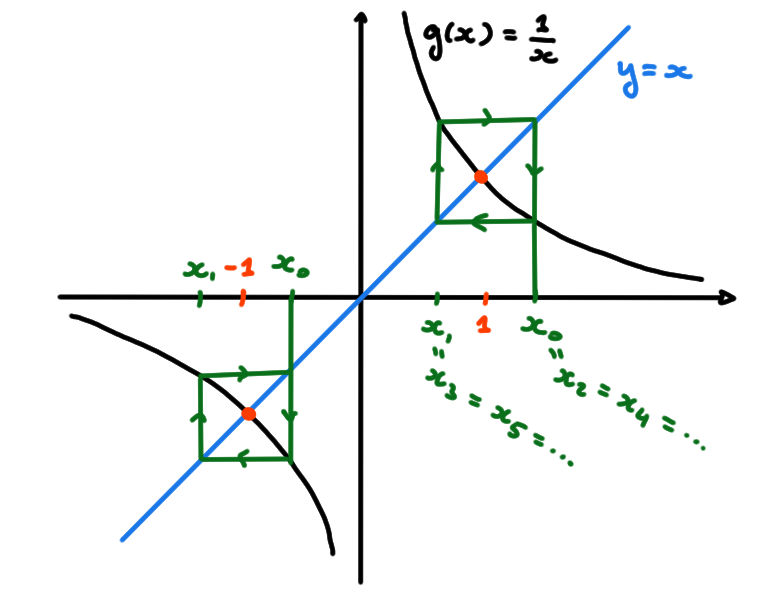
  3. \(x_0\in \mathbb{R}^*\), \(g(x):= \frac{1}{x}\).
  4. \(x_0\in \mathbb{R}\), \(g(x):= 4-x\).
  5. \(x_0\in \mathbb{R}\), \(g(x):= x^2+1\).
  6. \(x_0\in \mathbb{R}_+\), \(g(x):= x^2\).
  7. \(x_0\in \mathbb{R}\), \(g(x):= \cos(x)\).
  8. \(x_0\in \mathbb{R}\), \(g(x):= \begin{cases} \frac{x+1}{2}&\text{ si }x\lt 1\,, \\ \frac{x}{2}&\text{ si }x\geqslant 1\,. \end{cases} \)
On a vu ici que la connaissance du graphe de \(g\) permet d'obtenir des informations qualitatives utiles sur le comportement de la suite, en particulier dans la limite \(n\to \infty\).
Dans chaque cas, on devra distinguer le comportement de la suite en fonction de la condition initiale: si le comportement de la suite change en fonction de la condition initiale, on décrira ce changement.

L'interprétation graphique de la construction d'une suite définie par récurrence permet parfois, sans le moindre calcul, d'obtenir beaucoup d'informations, mais insistons sur le fait qu'elle ne représente pas une étude rigoureuse. Donc chacune des affirmations faites au sujet des suites ci-dessus, pour être validée, devrait en principe être complétée par une étude rigoureuse, comme vu au cours ou dans les exercices précédents.
On pourra tester toutes les suites avec l'animation ci-dessous:
  1. \(g(x)=\frac32-\frac12 x\):
    La suite n'est pas monotone, mais elle converge vers le point fixe de \(g\), \(x_n\to 1\), quelle que soit sa condition initiale.
  2. \(g(x)=2x-5\):
    La suite diverge dès que sa condition initiale est différente du point fixe de \(g\), donné par \(x_*=5\).
    • Si \(x_0\lt x_*\), alors \(x_n\to-\infty\).
    • Si \(x_0=x_*\), alors la suite est constante, \(x_n=x_*\) pour tout \(n\).
    • Si \(x_0\gt x_*\), alors \(x_n\to+\infty\).
  3. \(g(x)=\frac1x\):
    Remarquons que dans ce cas, \(x_1=\frac{1}{x_0}\), \(x_2=x_0\), \(x_3=\frac{1}{x_0}\), etc. Donc la suite ne converge pas, à moins que \(x_0\) soit un point fixe de \(g\), c'est-à-dire \(x_*=+1\) ou \(x_*=-1\):
  4. \(g(x)=4-x\):
    On a \(x_1=4-x_0\), \(x_2=4-x_1=4-(4-x_0)=x_0\), etc., donc la suite ne converge pas à moins que \(x_0=x_*=2\), le point fixe de \(g\), et dans ce cas c'est une suite constante.
  5. \(g(x)=x^2+1\):
    La suite tend vers l'infini, quelle que soit la condition initiale. Remarquons que \(g\) n'a pas de point fixe.
  6. \(g(x)=x^2\):
    Si \(|x_0|>1\), alors \(x_n\to+\infty\). Si \(x_0=\pm 1\), alors \(x_n=1\) pour tout \(n\). Finalement, si \(|x_0|\lt 1\), alors \(x_n\to 0\).
  7. \(g(x)=\cos (x)\):
    Dans ce cas, une analyse graphique n'est de loin pas suffisante, mais il semble que pour toute condition initiale \(x_0\), on a \(x_n\to x_*\), où \(x_*\) est le point fixe du cosinus, \(x_*=\cos(x_*)\) (équation transcendentale), dont la valeur approximative est \(x_*\simeq 0.739\).

    Suggestion: Sur votre calculatrice, choisissez une condition initiale quelconque \(x_0\), puis en appuyant de manière répétée sur ''\(\cos\)'', calculez les valeurs de \(x_1=\cos(x_0)\), \(x_2=\cos(\cos(x_0))\), etc., et observez que les valeurs de \(x_n\) semblent s'approcher (de façon non-monotone) d'un nombre \(0.739\cdots\)
  8. \(g(x):= \begin{cases} \frac{x+1}{2}&\text{ si }x\lt 1\,, \\ \frac{x}{2}&\text{ si }x\geqslant 1\,. \end{cases} \)
    On voit que \(g\) n'a pas de point fixe, mais pour toute condition initiale \(x_0\), \(x_n\to 1\).

    Ce comportement n'est pas en contradiction avec le résultat du cours (celui qui dit que ''si \(x_n\) converge, et si \(g\) est continue, alors \(x_n\) converge un point fixe de \(g\)''), puisque la fonction \(g\) n'est pas continue.