4.4 Approche graphique

La difficulté, dans l'étude d'une suite \(x_{n+1}=g(x_n)\), est parfois de savoir par où commencer. Montrer que la suite est majorée/minorée? Si oui, avec quel majorant/minorant? Montrer que la suite est croissante/décroissante?

Nous allons voir maintenant que le graphe de \(g\) peut être une aide précieuse dans cette analyse, et peut donner des pistes.

Remarque: L'approche graphique que nous allons présenter est utile car elle suggère des façons de commencer à étudier la suite, mais elle ne fournit en aucun cas une étude rigoureuse.

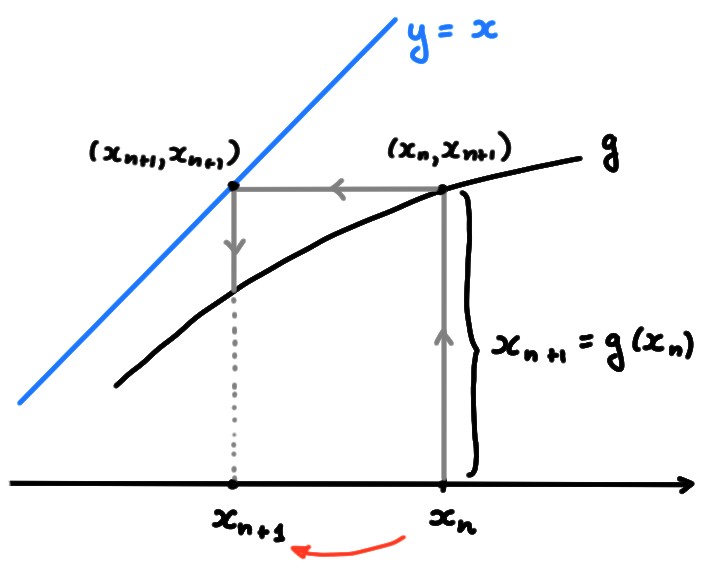
Supposons que le graphe de la fonction \(g\) est connu, et que la valeur de \(x_n\) a déjà été calculée. Montrons comment construire \(x_{n+1}\) graphiquement à partir de \(x_n\) et du graphe de \(g\):

  1. Commencer en \((x_n,0)\)
  2. Monter verticalement sur le graphe de \(g\), au point \((x_n,g(x_n))=(x_n,x_{n+1})\)
  3. Glisser horizontalement jusque vers la diagonale \(y=x\), au point \((x_{n+1},x_{n+1})\)
  4. Redescendre sur \((x_{n+1},0)\)

Bien-sûr, on peut sur le même dessin représenter \(x_{n+2}\) à partir de \(x_{n+1}\), etc. Donc en partant de \(x_0\), on a un moyen graphique de suivre la trajectoire \(x_0,x_1,x_2,\dots\)

Exemple: Reprenons le premier exemple considéré dans ce chapitre, associée à \[g(x)=1+\frac{x}{2}\,.\] Sur l'animation ci-dessous, observer le comportement de la suite en fonction de la condition initiale \(x_0\):

On observe graphiquement tout ce que nous avions obtenu analytiquement. En particulier, on voit le point fixe \(x_*=2\), à l'intersection entre le graphe de \(g\) et la droite \(y=x\). Puis, une fois la condition initiale \(x_0\) choisie,

Exemple: Considérons la suite traitée dans la section précédente, associée à \[g(x)=2-\frac1x\,,\] avec la condition initiale \(x_0=4\):

On remarque que le graphe de \(g\) est tangent à la diagonale au point fixe, et comme n'importe quelle condition initiale au-dessus du point fixe mène toujours à la même limite, qui est atteinte en décroissant, comme vu précédemment. D'autres conditions initiales mènent à la même limite, mais sans que la suite soit forcément monotone.

Exemple: Considérons la suite logistique de l'introduction, \[ x_{n+1}=rx_n(1-x_n)\,. \] L'animation ci-dessous montre les grandes différences dans le comportement asymptotique de la suite, en fonction de la valeur du paramètre \(r\gt 0\). (Pour ne pas rendre le dessin incompréhensible, on n'a représenté que les \(20\) premiers termes de la suite.)

Dernière compilation: 2024-12-04 (07:30:06)

Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)