Exercice 05-04
Considérer la suite \((a_n)\) définie par \(a_1:=\frac{5}{2}\) et, pour \(n\geqslant 1\), \[ a_{n+1}:=\frac{a_n^2+6}{5}\,. \]
  1. Montrer que \(2\leqslant a_n\leqslant 3\) pour tout pour tout \(n\geqslant 1\),
  2. Montrer que \((a_n)\) est décroissante,
  3. Conclure que \((a_n)\) converge et calculer sa limite.
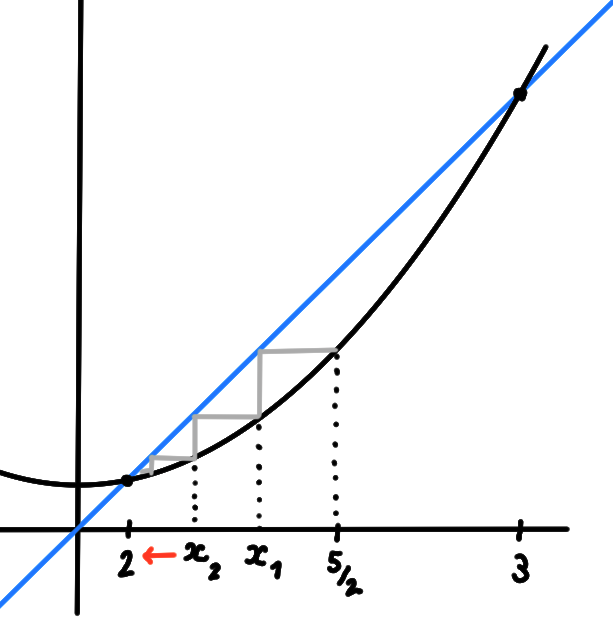
  4. Faire un croquis qui illustre graphiquement ce qui se passe.
Dans cet exercice on donne toutes les étapes qui mènent à une compréhension claire de ce que fait la suite. On suit la méthode qui a été décrite dans l'exemple détaillé ici dans le cas de \(g(x)=2-\frac{1}{x}\).

Montrer que \(2\leqslant a_n\leqslant 3\) par récurrence sur \(n\geqslant 1\).

Étudier \(a_{n+1}-a_n\), et utiliser 1.

Procéder comme au cours, en trouvant la valeur de la limite en prenant \(n\to \infty\) des deux côtés de la relation qui définit \(a_{n+1}\) en fonction de \(a_n\). Énoncer le résultat du cours utilisé.

  1. On procède par récurrence. Pour \(n=1\), on a \(2\leqslant a_1=\frac{5}{2}\leqslant 3\). Supposons alors que \(2\leqslant a_n\leqslant 3\). On a d'une part que \[ a_{n+1}=\frac{a_n^2+6}{5}\leqslant \frac{3^2+6}{5}=3\,, \] et d'autre part que \[ a_{n+1}=\frac{a_n^2+6}{5}\geqslant \frac{2^2+6}{5}=2\,, \] ce qui montre bien que \(2\leqslant a_{n+1}\leqslant 3\).
  2. On calcule \[\begin{aligned} a_{n+1}-a_n&=\frac{a_n^2+6}{5}-a_n\\ &=\tfrac{1}{5}(a_n^2-5a_n+6)\\ &=\tfrac15\underbrace{(a_n-3)}_{\leqslant 0}\underbrace{(a_n-2)}_{\geqslant 0}\leqslant 0\,, \end{aligned}\] donc \((a_n)\) est décroissante.
  3. Étant minorée (par \(2\)) et décroissante, \((a_n)\) converge: \[ \lim_{n\to \infty}a_n=L\,. \] Comme \(g(x)=\frac{x^2+6}{5}\) est continue, un théorème vu au cours garantit que \(L\) est un point fixe de \(g\), c'est-à-dire que \(L\) doit satisfaire \[ L=\frac{L^2+6}{5}\,. \] Cette dernière a pour solutions \(L_1=2\) et \(L_2=3\). Comme la suite est décroissante, on doit avoir \(L\leqslant a_1=\frac52\lt L_2\), la limite est donc \(L=L_1=2\).
  4. Illustrons la décroissance et la convergence vers le point fixe \(L=2\), à partir de la construction graphique de la suite vue au cours, et du graphe de \(g(x)=\frac{x^2+6}{5}\):
    Ce croquis montre tout ce qui est important: les deux points fixes, la condition initiale, la décroissance de la suite, ainsi que la convergence vers la limite. Mais le dessin n'est évidemment pas à l'échelle.