Exercice 13-09
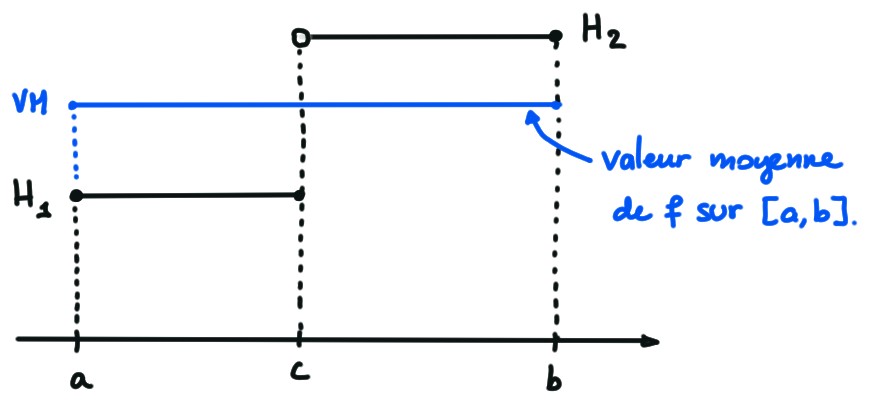
Soient \(a\lt c\lt b\), et \(f:[a,b]\to \mathbb{R}\) définie par \[ f(x):= \begin{cases} H_1&\text{ si }a\leqslant x\leqslant c\,,\\ H_2&\text{ si }c< x\leqslant b\,,\\ \end{cases} \] où \(H_1,H_2\) sont deux constantes.
  1. Calculer \(\overline{f}\) (valeur moyenne de \(f\) sur \([a,b]\)).
  2. Existe-t-il un \(c_*\in [a,b]\) tel que \(f(c_*)=\overline{f}\)?
Le but de cet exercice est de voir que la conclusion du Théorème de la Moyenne n'est plus vraie sans l'hypothèse de continuité.

Pour 2, on distinguera les cas \(H_1= H_2\), \(H_1\neq H_2\).
  1. Comme \(f\) est constante par morceaux, elle est intégrable, et \[\begin{aligned} \int_a^bf(x)\,dx &= \int_a^cf(x)\,dx+ \int_c^bf(x)\,dx\\ &=H_1(c-a)+H_2(b-c)\,. \end{aligned}\] Donc \[ \overline{f}=\frac{1}{b-a}\int_a^b f(x)\,dx= \frac{c-a}{b-a}H_1+\frac{b-c}{b-a}H_2\,. \]
  2. Dans le cas où \(H_1=H_2\), la réponse est ''oui'', puisque \(f\) est constante, et donc \(\overline{f}=H_1=H_2\), et \(c_*\) peut être n'importe quel point de \(]a,b[\): \(f(c_*)=\overline{f}\).

    Mais si \(H_1\neq H_2\), par exemple \(H_1\lt H_2\), alors \(f\) est discontinue en \(c\). De plus, \[ H_1\lt \overline{f}\lt H_2\,, \] et comme il n'existe aucun \(x\in ]a,b[\) où la fonction prend une valeur intermédiaire entre \(H_1\) et \(H_2\), on conclut qu'il n'existe aucun point \(c_*\) avec la propriété requise.