Analyse 1 | S. Friedli (EPFL)

12.4 Le Théorème de la Moyenne

La moyenne d'une fonction?

En arithmétique, on définit la moyenne d'une famille de nombres \(x_1,x_2,\dots,x_N\) par \[ \bar x:= \frac1N\bigl(x_1+x_2+\dots+x_N\bigr) \] Si on veut calculer la valeur moyenne d'une fonction \(f:[a,b]\to \mathbb{R}\), on ne peut pas simplement sommer ses valeurs , et on a naturellement recours à l'intégrale:

Si \(f:[a,b]\to \mathbb{R}\) est intégrable, on définit sa valeur moyenne sur \([a,b]\) par \[ \bar f:= \frac{1}{b-a}\int_a^bf(x)dx\,. \]

\(\bar f\) est l'analogue continu de la moyenne discrète \(\bar x\). En effet,

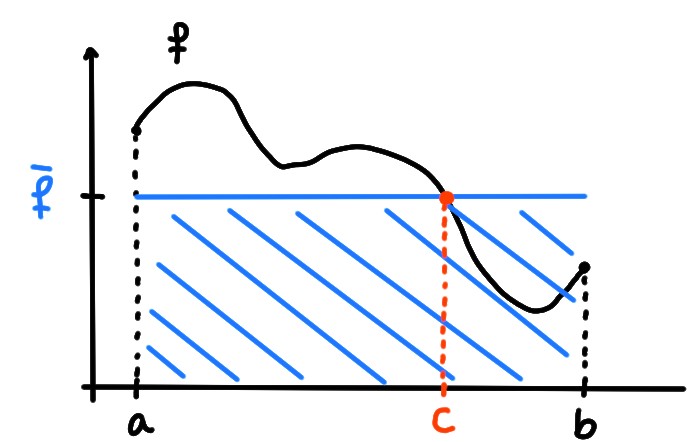
à la somme des \(x_k\), \(k\in \{1,\dots,N\}\) correspond l'intégrale des \(f(x)\), \(x\in [a,b]\), et
à la division par la taille de l'échantillon, \(\frac1N\), correspond la division par la longueur de l'intervalle \(\frac{1}{b-a}\).

Lorsque \(f(x)\geqslant 0\), on peut interpréter le nombre \(\bar f\) géométriquement: c'est l'unique nombre tel que le rectangle de base \([a,b]\) et de hauteur \(\bar f\) ait même aire que la région sous la courbe.

Supposons que la région sous le graphe de \(f\) est une forme faite de glace, contenue dans un récipient de base \([a,b]\); la quantité de glace présente dans cette forme est égale à \[\int_a^bf(x)\,dx\,.\] Si on laisse la glace fondre, après un certain temps, toute la glace s'est transformée en eau, dont le niveau dans le récipient est à une certaine hauteur \(\bar f\). Puisque la quantité d'eau est (en première approximation) égale à la quantité de glace initiale, on doit avoir \[ (b-a)\bar f=\int_a^bf(x)\,dx\,. \] Le niveau d'eau coïncide donc avec la valeur moyenne de \(f\).

Théorème: (Théorème de la moyenne) Si \(f:[a,b]\to \mathbb{R}\) est continue, alors il existe \(c\in ]a,b[\) tel que \[f(c)=\frac{1}{b-a}\int_a^bf(x)dx\,.\]

Preuve:

Comme \(f\) est continue, elle atteint une valeur minimum \(m\) et une valeur maximum \(M\); de plus, \(\mathrm{Im} (f)=[m,M]\), ce qui implique \(m\leqslant f(x)\leqslant M\) pour tout \(x\in [a,b]\), et donc aussi \[ \int_a^bm\,dx \leqslant \int_a^bf(x)dx\leqslant \int_a^bM\,dx\,, \] ce qui donne, après division par \(b-a\), \[ m\leqslant \bar f\leqslant M\,. \] Mais comme \(\mathrm{Im} (f)=[m,M]\), le Théorème de la valeur intermédiaire implique qu'il existe au moins un \(c\in ]a,b[\) tel que \(f(c)=\bar f\).

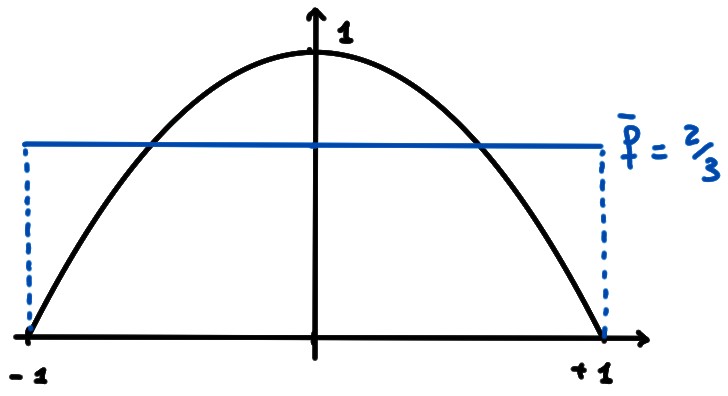
Exemple: Considérons encore la parabole d'Archimède, qui est le graphe de la fonction continue \(f(x)=1-x^2\), \(x\in [-1,1]\). Sa valeur moyenne est donnée par \[ \bar f=\frac{1}{1-(-1)}\int_{-1}^1(1-x^2)\,dx=\frac12\cdot \frac43=\frac23\, \]

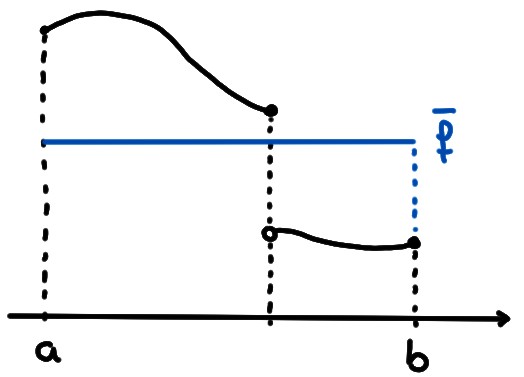
On voit qu'il existe deux nombres, \(\overline{c}=\pm\frac{1}{\sqrt{3}}\in]-1,1[\), tels que \(f(c)=\overline{f}\).

Remarque: Remarquons que si \(f\) n'est pas continue, alors le résultat n'est pas toujours vrai:

Cette fonction est manifestement continue par morceaux, donc intégrable, et sa valeur moyenne \(\bar f\) est bien définie. Par contre, il n'existe aucun \(c\in ]a,b[\) tel que \(f(c)=\bar f\).