Étudier la convergence de la série
\[
\sum_{n\geqslant 1}\frac{1}{\sqrt{1}+\sqrt{2}+\cdots+\sqrt{n}}
\]
Ce genre de série est difficile à étudier avec les techniques classiques vues
dans le
chapitre sur les séries,
parce que son terme général lui-même implique une somme. (Aucun critère simple
pour les séries ne permet de voir facilement si cette série converge ou
diverge.)
Pour commencer
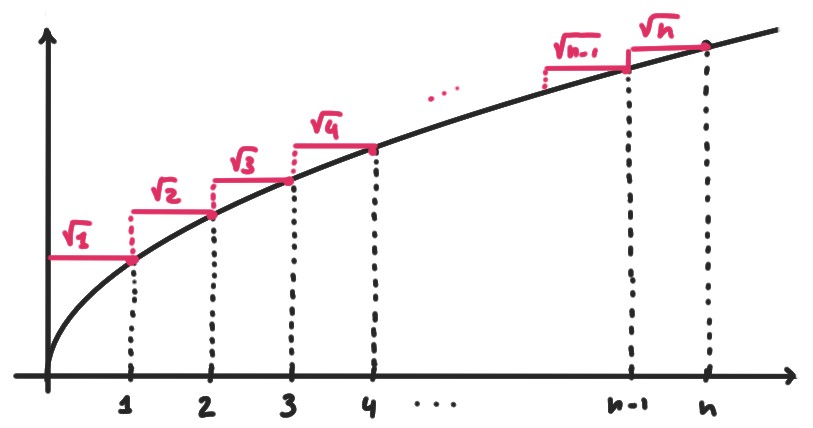
Comparer la somme \(\sqrt{1}+\sqrt{2}+\cdots+\sqrt{n}\) à une intégrale.
On minore le numérateur du terme général \(a_n\), en remarquant que
\[ \sqrt{1}+\sqrt{2}+\sqrt{3}+\cdots+\sqrt{n-1}+\sqrt{n}\geqslant
\int_0^n\sqrt{x}\,dx=\frac23 n^{3/2}\,,
\]
ce qui permet de majorer le terme général de la série de départ comme suit:
\[
0\leqslant a_n=
\frac{1}{\sqrt{1}+\sqrt{2}+\cdots+\sqrt{n}}
\leqslant \frac32 \frac{1}{n^{3/2}}
\]
Puisque la série \(\sum_n\frac{1}{n^{3/2}}\) est convergente (\(p=3/2\gt 1\)),
on conclut que \(\sum_na_n\) converge aussi.