Analyse 1 MATH-101(c)

On a vu ici comment obtenir le développement limité d'ordre

n

autour de

x_0=0

d'une fonction composée

g\circ h

, lorsqu'on possède des développements limités pour

h

(autour de

x_0=0

) et de

g

(autour de

u_0=h(0)

\begin{aligned} h(x)&=b_0+b_1x+b_2x^2+\cdots+b_nx^n+x^n\varepsilon_h(x)\,\\ g(u)&=a_0+a_1(u-u_0)+a_2(u-u_0)^2+\cdots+a_n(u-u_0)^n+(u-u_0)^n\varepsilon_g(u) \end{aligned}

On a expliqué comment obtenir la partie principale du développement de

g\circ h

. Pour 1.

L'avantage ici est que $h$ est une fonction qui est déjà sous forme polynomiale. On a vu un exemple très semblable au cours.

Pour 2.

Lorsque $x$ est petit, $\cos(x)$ est proche de $1$ . Donc on aura avantage à voir la fonction comme suit: $\log(\cos(x))=\log\big(1+\underbrace{(\cos(x)-1)}_{=:u}\bigr)$

Comme $\frac{1}{1+2x^3}$ est la composée de $g(u)=\frac{1}{1-u}$ (dont on connaît le développement limité) avec $h(x)=-2x^3$ . Lorsque $x$ est au voisinage de $x_0=0$ , les valeurs de $h(x)$ sont petites et donc on peut directement injecter $h(x)$ dans le développement limité de $g$ . Puisqu'on veut un $DL(6)$ , et que $h$ est de degré $3$ , il suffit de garder pour $g$ un $DL(2)$ : $\begin{aligned} \frac{1}{1+2x^3} &=\frac{1}{1-u}\Big|_{u=-2x^3}\\ &=1+u+u^2+u^2\varepsilon(u)\Big|_{u=-2x^3}\\ &=1-2x^3+4x^6+(-2x^3)^2\varepsilon(-2x^3)\\ &=1-2x^3+4x^6+x^6\underbrace{4\varepsilon(-2x^3)}_{\tilde\varepsilon(x)}\\ \end{aligned}$ où $\tilde\varepsilon(x)\to 0$ lorsque $x\to 0$ .

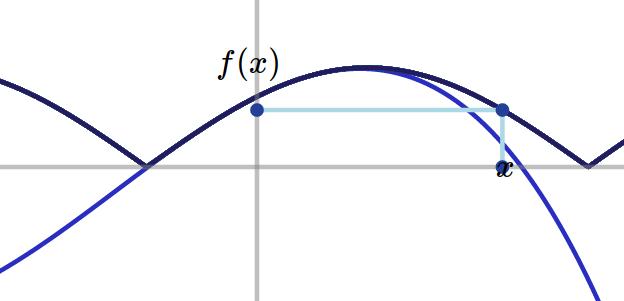
En bleu, la partie principale: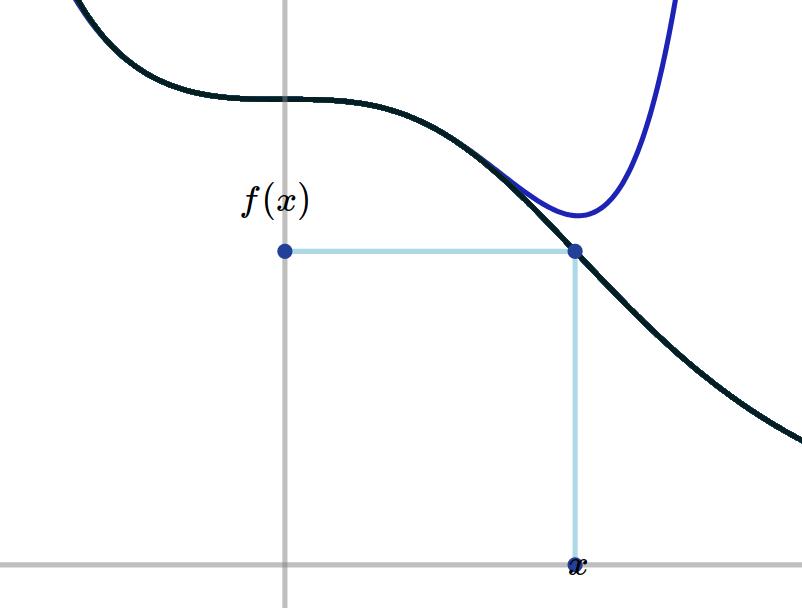
Lorsque $x$ est proche de $0$ , $\cos(x)$ est proche de $1$ , donc $\cos(x)-1$ est proche de $0$ . Il est donc plus judicieux d'écrire $f(x)= \log(\cos(x)) =\log\big(1+\underbrace{(\cos(x)-1)}_{=:u}\bigr)\,,$ et penser à $u$ comme étant une quantité petite. En fait, la petitesse de $u$ est en $x^2$ , puisque le $DL(4)$ autour de $0$ est donné par $u=h(x)=\cos(x)-1 =-\frac{x^2}{2!}+\frac{x^4}{4!} + x^4\varepsilon_c(x)\,.$ On sait que $f(u)=\log(1+u)$ a son $DL(4)$ autour de $u=0$ donné par $\log(1+u) = u-\frac{u^2}{2}+\frac{u^3}{3}-\frac{u^4}{4}+ u^4\varepsilon_l(u)\,.$ On pourrait injecter la partie principale du développement limité de $\cos(x)-1$ (dont le terme de plus petit degré est $x^2$ ) dans celle de $\log(1+u)$ , mais remarquons d'abord que
- le terme $\frac{u^3}{3}$ va donner des termes en $x^6$ , et
- le terme $\frac{u^4}{4}$ va donner des termes en $x^8$ .
Donc les termes $+\frac{u^3}{3}-\frac{u^4}{4}$ ne vont donner aucune contribution à la partie principale du développement que nous voulons pour $f(x)$ .

Il suffit donc d'utiliser simplement un $DL(2)$ : $\log(1+u) = u-\frac{u^2}{2}+ u^2\varepsilon_l(u)\,.$ Maintenant, en injectant une partie principale dans l'autre, $\begin{aligned} \left.u-\frac{u^2}{2}\right|_{u=-\frac{x^2}{2!}+\frac{x^4}{4!}} &=\left(-\frac{x^2}{2!}+\frac{x^4}{4!}\right)- \frac{1}{2}\left( -\frac{x^2}{2!}+\frac{x^4}{4!}\right)^2\\ &=-\frac{1}{2}x^2-\frac{1}{12}x^4+\underbrace{\frac{x^6}{2\cdot 4!}-\frac{x^8}{2\cdot 4!}}_{\text{degré}\gt 4} \end{aligned}$ On obtient donc $\begin{aligned} f(x)=\log(\cos(x)) =-\frac{1}{2}x^2-\frac{1}{12}x^4+x^4\varepsilon(x) \end{aligned}$ En bleu, la partie principale: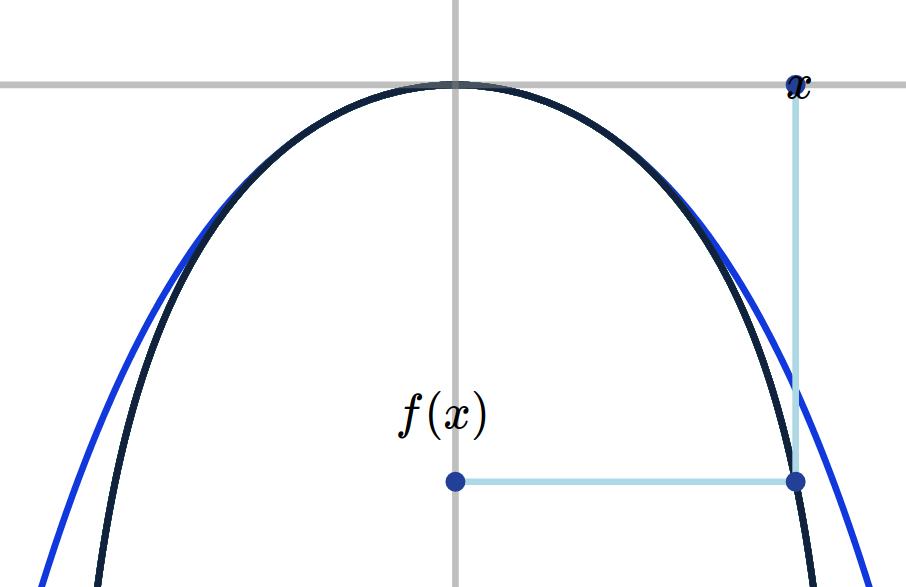
Le $DL(4)$ autour de $x_0=0$ : $h(x)=\sin(x) ={\color{green}x-\frac{x^3}{3!}+x^4\varepsilon_s(x)}\,.$ Puis, le $DL(4)$ autour de $u_0=h(0)=0$ : $\begin{aligned} e^u &=1+u+\dfrac{u^2}{2!}+\dfrac{u^3}{3!}+\dfrac{u^4}{4!}+u^4\varepsilon_e(u) \\ \end{aligned}$ Ainsi, en insérant la partie principale du sinus dans celle de l'exponentielle, $\begin{aligned} 1+u+\dfrac{u^2}{2!}+&\dfrac{u^3}{3!}+\dfrac{u^4}{4!}\Big|_{u={\color{green}x-\frac{x^3}{3!}}}\\ =&1 +\left({\color{green}x-\frac{x^3}{6}}\right) +\frac{1}{2}\left({\color{green}x-\frac{x^3}{3!}}\right)^2\\ &\phantom{xxxxx}+\frac{1}{6}\left({\color{green}x-\frac{x^3}{3!}}\right)^3 +\frac{1}{24}\left({\color{green}x-\frac{x^3}{3!}}\right)^4\\ =& 1+\left(x-\frac{x^3}{6}\right) + \frac{1}{2}\left(x^2-\frac{x^4}{3}\right) + \frac{1}{6}x^3+ \frac{1}{24}x^4 + \underbrace{\left(\dots\right)}_{\text{degré}>4} \end{aligned}$ On conclut donc que $\exp(\sin(x)) = 1+x+\frac{x^2}{2}-\frac{x^4}{8}+ x^4\varepsilon(x)\,.$ En bleu, la partie principale:
On a $\sqrt{1+\sin(x)}=g(h(x))$ , où $h(x)=\sin(x)$ , $g(u)=\sqrt{1+u}$ . Lorsque $x$ est proche de zéro, $u=h(x)=\sin(x)$ est proche de zéro aussi.

Les développements limités d'ordre $3$ sont, autour de $x_0=0$ : $\sin(x)=x-\frac{x^3}{6}+ x^3\varepsilon_s(x)\,,$ autour de $u=0$ , $\sqrt{1+u}=1+\frac{u}{2} -\frac{u^2}{8} + \frac{u^3}{16} + u^3\varepsilon_r(u)\,.$ En injectant une partie principale dans l'autre, $\begin{aligned} 1+\frac{u}{2} &-\frac{u^2}{8} + \frac{u^3}{16}\Big|_{u=x-\frac{x^3}{6}}\\ &= 1+\frac{1}{2}\left(x-\frac{x^3}{6}\right) -\frac{1}{8}\left(x-\frac{x^3}{6}\right)^2 \\ &\quad\; + \frac{1}{16}\left(x-\frac{x^3}{6}\right)^3\\ &= 1 + \frac{x}{2} - \frac{x^2}{8} -\frac{x^3}{48}+ \underbrace{\left(\dots\right)}_{\text{degré}>4} \,. \end{aligned}$ En bleu, la partie principale:

Exercice 12-06