On dit qu'une fonction
f:[a,b]→R possède
la propriété de l'accroissement fini
si il existe un point
c∈]a,b[ où
f est dérivable
et où
f′(c)=b−af(b)−f(a).
Déterminer, parmi les fonctions suivantes, celles qui possèdent la
propriété de
l'accroissement fini. Lorsque c'est le cas, on donnera si possible la valeur de
c.
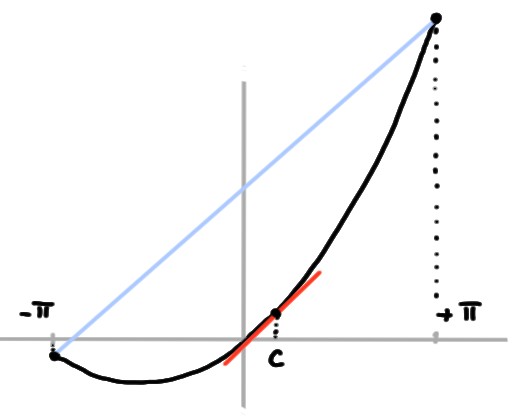
- f(x)=xex sur [−π,π]
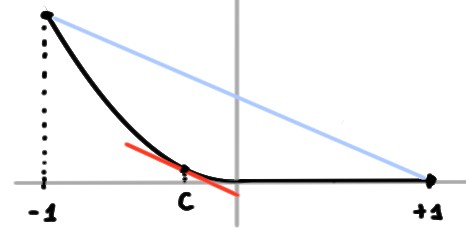
- f(x)={x20 si −1⩽x<0, si 0⩽x⩽1.
- f(x)={x22x si −1⩽x<0, si 0⩽x⩽1.
- f(x)=∣x∣ sur [−1,1]
Attention à bien relire l'énoncé!
Remarquons que
le Théorème des accroissements finis (TAF)
affirme que si
f:[a,b]→R satisfait aux hypothèses suivantes (appelées
''hypothèses du TAF''),
- f est continue sur [a,b],
- dérivable sur ]a,b[,
alors elle possède la propriété de l'accroissement fini définie dans l'énoncé.
Dans les cas considérés ici, on pourra parfois utiliser le TAF, parfois pas.