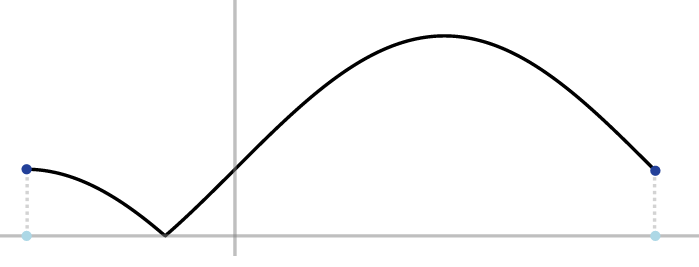
- \(f\) étant dérivable, elle est continue, et
ses points stationnaires, s'il y en a, sont ceux où sa dérivée s'annule.
Or
\[ f'(x)=2xe^x+x^2e^x=x(x+2)e^x\,.\]
Cette dernière s'annulle en \(x=0\), où \(f(0)=0\), et en \(x=-2\), où
\(f(-2)=4e^{-2}\).
Sur les bords, \(f(-3)=9e^{-3}\), \(f(1)=e\). Ainsi, \(f\) atteint son minimum en \(x_*=0\). Aussi,- \(f(1)\gt f(-3)\) car \(e\gt 9e^{-3}\) (puisque \(e^4\gt 9\)), et
- \(f(1)\gt f(-2)\) car \(e\gt 4e^{-2}\) (puisque \(e^3\gt 4\)).
Puisque \(f\) est continue, on a aussi que \(\mathrm{Im} (f)=[0,e]\).
- Commençons par remarquer que \(f\) est continue et que
\(\sin(x)+\frac12=0\) si et seulement si
\(x=-\frac{\pi}{6}+2k\pi\) ou \(x=\frac{7\pi}{6}+2k\pi\). Donc
\[ \sin(x)+\tfrac12
\begin{cases}
\lt 0&\text{ si }-\frac{\pi}{2}\leqslant x\lt -\frac{\pi}{6}\\
\geqslant 0&\text{ si }-\frac{\pi}{6}\leqslant x\leqslant \pi\,,
\end{cases}
\]
Ainsi,
\[f(x)=
\begin{cases}
-(\sin(x)+\tfrac12)&\text{ si }-\frac{\pi}{2}\leqslant x\lt -\frac{\pi}{6}\\
\sin(x)+\tfrac12&\text{ si }-\frac{\pi}{6}\leqslant x\leqslant \pi\,.
\end{cases}
\]
Les points stationnaires de \(f\) sur
\(]-\frac{\pi}{2},\pi[\) sont ceux où \(f\) n'est soit pas
dérivable, soit dérivable de dérivée nulle.
Or
\[f'(x)=
\begin{cases}
-\cos(x)&\text{ si }-\frac{\pi}{2}\lt x\lt -\frac{\pi}{6}\\
\cos(x)&\text{ si }-\frac{\pi}{6}\lt x\lt \pi\,,
\end{cases}
\]
qui donne comme unique point
de \(]-\frac{\pi}{2},\pi[\) où \(f\) est dérivable et sa dérivée s'annule,
\(f'(\frac{\pi}{2})=0\). De plus,
\[\begin{aligned}
\lim_{x\to-\frac{\pi}{6}^-}f'(x)&=-\tfrac{\sqrt{3}}{2}\,,\\
\lim_{x\to-\frac{\pi}{6}^+}f'(x)&=+\tfrac{\sqrt{3}}{2}\,,\\
\end{aligned}\]
et donc
\(f\) n'est pas dérivable en \(-\frac{\pi}{6}\).
Stationnaires: \(f(-\frac{\pi}{6})=0\), \(f(\frac{\pi}{2})=\frac32\).
Sur le bord, \(f(-\frac{\pi}{2})=\frac12\), \(f(\pi)=\frac12\).
On conclut que \(f\) atteint son minimum en \(x_*=-\frac{\pi}{6}\), et son maximum en \(x^*=\frac{\pi}{2}\).Puisque \(f\) est continue, on sait que \(\mathrm{Im} (f)=[0,\frac32]\).