Exercice 09-03
Étudier la continuité des fonctions \(f\colon\mathbb{R}\to\mathbb{R}\) ci-dessous, au point \(x_0=0\):
  1. \( f(x)= \begin{cases} \frac{1}{1 + 2^{1/x}} & x\neq 0 \\ 1 & x=0 \end{cases} \)
  2. \( f(x) = \begin{cases} \frac{1-\cos(x)}{x^2} &x\neq 0 \\ \frac{1}{2} &x=0 \end{cases} \)
  3. \(f(x)= \begin{cases} \cos(1/x)&x\neq 0 \\ 0 & x=0 \end{cases} \)
  4. \( f(x)= \begin{cases} x\cdot \sin (\frac1x) &x\neq 0 \\ 0 & x=0 \end{cases} \)
Rappelons qu'une fonction \(f\) est continue en \(x_0=0\) si sa limite \(\lim_{x\to 0} f(x)\) existe et vaut \[ \lim_{x\to 0} f(x)=f(0)\,. \] Si la structure de la fonction le suggère, on pourra séparer l'étude de la limite \(x\to x_0\) en ses deux versions latérales. Ceci mènera éventuellement à une notion de continuité latérale, plus faible.
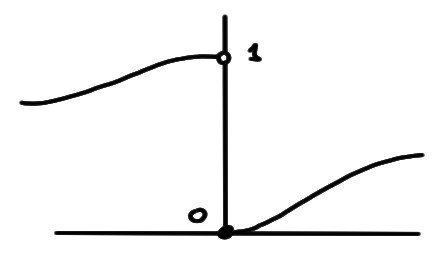
  1. On calcule les limites latérales lorsque \(x\to 0\), en introduisant \(u=\frac1x\), \[ \lim_{x\to 0^-}f(x) =\lim_{u\to -\infty}f\left(\tfrac{1}{u}\right)= \lim_{u\to -\infty}\frac{1}{1+2^u}=1=f(0)\,. \] \[ \lim_{x\to 0^+}f(x) =\lim_{u\to \infty}f\left(\tfrac{1}{u}\right) =\lim_{u\to\infty}\frac{1}{1+2^u}=0\neq f(0)\,. \] Donc \(f\) n'est pas continue mais seulement continue à gauche en \(x=0\):
  2. On calcule \[\begin{aligned} \lim_{x\to 0}f(x) &= \lim_{x\to 0}\frac{1-\cos(x)}{x^2}\\ &= \lim_{x\to 0}\frac{1-\cos(x)^2}{x^2\big(1+\cos(x)\big)}\\ &= \lim_{x\to 0}\left(\frac{\sin(x)}{x}\right)^2 \cdot\lim_{x\to 0}\frac{1}{1+\cos(x)} \\ &=1^2 \cdot \frac{1}{2} = \frac{1}{2}= f(0), \end{aligned}\] Ainsi \(f\) est continue en \(x=0\).
  3. Considérons les suites \((x_n)\) et \((y_n)\) définies respectivement par \(x_n=\frac{1}{2n\pi}\) et \(y_n=\frac{1}{\frac{\pi}{2}+2n\pi}\). Alors \(\lim_{n\to\infty} x_n=0=\lim_{n\to\infty}y_n\), mais \[ \lim_{n\to\infty}f(x_n)=\lim_{n\to\infty}\cos(2n\pi)=1\,, \] et \[ \lim_{n\to\infty}f(y_n) =\lim_{n\to\infty}\cos\big(\tfrac{\pi}{2}+2n\pi\big)=0\,. \] Ainsi \(\lim_{x\to 0}f(x)\) n'existe pas et \(f\) n'est pas continue en \(x=0\).
  4. Comme la fonction sinus prend des valeurs dans \([-1,1]\), on a \[ -|x|\leqslant x\cdot \sin\!\left(\frac{1}{x}\right)\leqslant |x|. \] Par le théorème des deux gendarmes, puisque \(\lim\limits_{x\to 0}|x|=0\), on a \[ \lim_{x\to 0}\left(x\cdot \sin\!\left(\frac{1}{x}\right)\right)=0 = f(0). \] Ainsi \(f\) est continue en \(x=0\).