Exercice 09-04
Les fonctions ci-dessous sont-elle continues sur \(\mathbb{R}\)?
  1. \(\displaystyle f(x)= \begin{cases} \dfrac{x^3-1}{x-1} & \text{ si }x\gt 1\,, \\ 3&\text{ si }x=1\,,\\ \dfrac{\sin(x-1)}{2x-2}\,, & \text{ si }x\lt 1\,, \end{cases} \)
  2. \(g(x)=\lfloor x\rfloor\)
  3. ⚡ \(h(x)= \begin{cases} x^2&\text{ si }x\in \mathbb{Q}\,,\\ 1-x^2&\text{ si }x\in \mathbb{R}\setminus\mathbb{Q}\,. \end{cases} \)
Rappelons qu'une fonction \(f\) est continue sur \(\mathbb{R}\) si pour tout \(x_0\in \mathbb{R}\), sa limite \(\lim_{x\to x_0} f(x)\) existe et vaut \[ \lim_{x\to x_0} f(x)=f(x_0)\,. \] Pour une fonction donnée, il s'agit donc de savoir si tous les points \(x_0\in \mathbb{R}\) sont des points de continuité.

Si la structure de la fonction le suggère, on pourra séparer l'étude de la limite \(x\to x_0\) en ses deux versions latérales. Ceci mènera éventuellement à une notion de continuité latérale, plus faible.

La nature de cette fonction suggère d'étudier la continuité séparément, en les points de \(\mathbb{Z}\), puis en ceux de \(\mathbb{R}\setminus\mathbb{Z}\).

Même si le graphe de cette fonction a un graphe qu'il est impossible de tracer, un petit croquis montre clairement les points où cette fonction a une chance d'être continue.

  1. En dehors de \(1\), \(f\) est continue puisque c'est une composition de fonctions élémentaires qui sont continues sur leur domaine de définition. Il reste donc à voir si \(f\) est continue en \(x_0=1\), c'est-à-dire si \[\lim_{x\to 1}f(x)=f(1)\,.\] Or dans ce cas, la limite représente une indétermination ''\(\frac00\)'', puisque le polynôme \(x^3-1\) s'annule en \(x=1\). On peut donc le factoriser: \[x^3-1=(x-1)(x^2+x+1)\,,\] qui permet de calculer: \[\begin{aligned} \lim_{x\to 1^+}f(x)&= \lim_{x\to 1^+}\frac{x^3-1}{x-1}\\ &=\lim_{x\to 1^+}\frac{(x-1)(x^2+x+1)}{x-1}\\ &=\lim_{x\to 1^+}(x^2+x+1)=3\,. \end{aligned}\] D'autre part, \[\begin{aligned} \lim_{x\to 1^-}f(x) &=\lim_{x\to 1^-}\frac{\sin(x-1)}{2(x-1)}\\ &=\lim_{z\to 0^-}\frac{\sin(z)}{2(z)}\\ &= \frac{1}{2}\,. \end{aligned}\] Puisque \(\lim_{x\to 1^-}f(x)\neq \lim_{x\to 1^+}f(x)\), \(f\) ne peut pas être continue en \(1\). Ainsi \(f\) est discontinue en \(x=1\).

    Remarquons quand-même que \(f(1)=3\), donc \(f\) est continue à droite en \(1\).
  2. Il est naturel de distinguer les points \(x_0\) entiers des autres.

    Pour commencer, si \(x_0\in \mathbb{R}\setminus\mathbb{Z}\), alors \(g\) est constante dans un voisinage de \(x_0\): \[ g(x_0\pm \varepsilon)=\lfloor x_0\pm \varepsilon\rfloor=\lfloor x_0\rfloor \] pour tout \(\varepsilon>0\) suffisamment petit. Donc \[ \lim_{\varepsilon\to 0}g(x+\varepsilon)=g(x_0), \] ce qui signifie que \(g\) est continue en \(x_0\).

    Si \(x_0\) est entier, \(x_0=n\), \(n\in \mathbb{Z}\), alors pour tout \(\varepsilon>0\) suffisamment petit, \[ g(x_0+\varepsilon)=\lfloor x_0+\varepsilon\rfloor =x_0\,, \] et \[g(x_0-\varepsilon)=\lfloor x_0-\varepsilon\rfloor =x_0-1\] En particulier, \(g\) est continue à droite en \(x_0\) puisque \[ \lim_{x\to x_0^+}g(x)=x_0=g(x_0)\,, \] mais \[ \lim_{x\to x_0^-}g(x)=x_0-1=g(x_0)-1 \neq g(x_0)\,, \] et donc \(g\) est discontinue en \(x_0\).

    Donc \(g\) est discontinue mais continue à droite en chaque \(x_0\in \mathbb{Z}\), et continue partout ailleurs.
  3. On ne peut pas tracer simplement le graphe de cette fonction, mais un croquis peut quand-même aider à comprendre ce qui se passe:
    Sur cette image: si un point est bleu, c'est que sa première composante est rationnelle; s'il est rose c'est que sa première composante est irrationnelle.

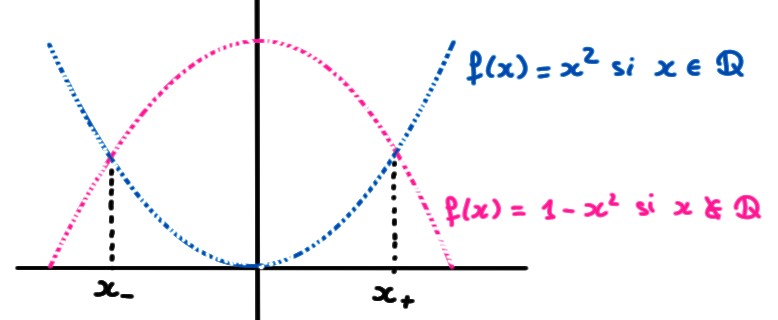
    Remarquons que les courbes \(y=x^2\) et \(y=1-x^2\) s'intersectent en exactement deux points: \(x_\pm=\pm \frac{\sqrt{2}}{2}\). Comme \[\lim_{x\to x_\pm}(1-x^2)= \lim_{x\to x_\pm}x^2, \] on en déduit que \(h\) est continue en ces deux points. Or \(h\) est discontinue en tout autre point \(x_0\not\in \{x_-,x_+\}\), puisque l'on peut toujours trouver une suite de rationnels \(x_n\in \mathbb{Q}\), \(x_n\to x_0\), pour laquelle \[ \lim_{n\to\infty}h(x_n)=\lim_{n\to\infty}x_n^2=x_0^2, \] et une suite d'irrationnels \(y_n\in \mathbb{R}\setminus \mathbb{Q}\), \(y_n\to x_0\), pour laquelle \[ \lim_{n\to\infty}h(y_n)=\lim_{n\to\infty}1-y_n^2=1-x_0^2\neq x_0^2\,.\]