On a vu au cours que pour trouver les racines \(n\)èmes de \(\omega\), on peut commencer par mettre \(\omega\) sous forme polaire/exponentielle, \(\omega=se^{\mathsf{i} \varphi}\). Ensuite, les racines sont \[ z_k=\sqrt[n]{s}e^{\mathsf{i} \frac{\varphi+2k\pi}{n}}\,\quad k\in\{0,1,2,\dots,n-1\}\,. \]

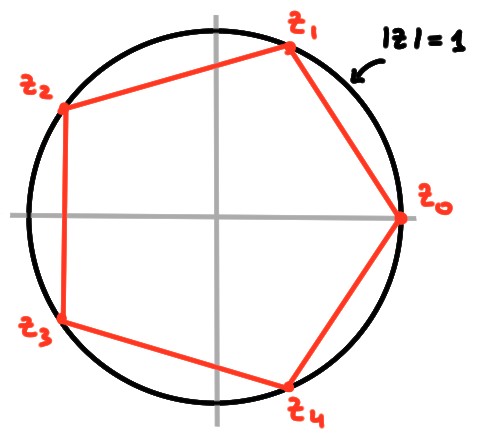
1. Sous forme polaire, \(\omega=1=1\cdot e^{\mathsf{i} 0}\), donc les racines \(5\)èmes sont \[z_{k}=e^{\mathsf{i}\frac{2\pi k}{5}}\,,\qquad k\in \{0,1,2,3,4\}\,.\] Celles-ci sont les sommets d'un pentagone centré à l'origine, de rayon \(1\):
   
2. Écrivons \(\omega=-3+4\mathsf{i}\) sous forme polaire/exponentielle. Puisque \(|\omega|=\sqrt{(-3)^2+4^2}=5\), on l'écrit comme \[ \omega=5\left(\frac{-3}{5}+\mathsf{i} \frac{4}{5}\right) \] Considérons un angle \(\theta\) qui satisfait \(\cos(\theta)=-\frac{3}{5}\) et \(\sin(\theta)=\frac{4}{5}\). Puisque \(\cos(\theta)\lt 0\) et \(\sin(\theta)\gt 0\), on peut choisir cet angle tel que \(\frac{\pi}{2}\lt \theta\lt \pi\), Ainsi, si on veut l'exprimer précisément: \(\theta=\arccos(-3/5)\). Maintenant, \[ \omega=5e^{\mathsf{i} \theta}\,, \] et ses racines carrées sont \[ z_k=\sqrt{5}\,e^{\mathsf{i}(\frac{\theta}{2} + \pi k)}\,\quad k\in\{0,1\}\,, \] c'est-à-dire \[ z_0=+\sqrt{5}e^{\mathsf{i}\frac{\theta}{2}}\,,\qquad z_1=-\sqrt{5}e^{\mathsf{i}\frac{\theta}{2}}\,.\qquad \] Puisque \(\frac{\pi}{2}\lt \theta\lt \pi\), on a \(\frac{\pi}{4}\lt \frac{\theta}{2}\lt \frac{\pi}{2}\), ce qui implique que \(\cos(\frac{\theta}{2})\gt 0\) et \(\sin(\frac{\theta}{2})\gt 0\).
   
   On peut être plus explicite en utilisant la relation trigonométrique \[ \cos^2(\theta/2)=\frac{1+\cos(\theta)}{2}=\frac{1-\frac35}{2}=\frac{1}{5}\, \] donc \(\cos(\frac{\theta}{2})=\frac{1}{\sqrt{5}}\) et \(\sin(\frac{\theta}{2})=\frac{2}{\sqrt{5}}\), ce qui donne comme solutions \[z_0=1+2\mathsf{i}, \qquad z_1=-1-2\mathsf{i}\,.\] On tombe directement sur cette solution explicite en utilisant des coordonnées cartésiennes. En effet, en posant \(z=a+\mathsf{i} b\), l'équation donnée devient \[a^2-b^2+2ab\mathsf{i}=-3+4\mathsf{i}\,,\] qui mène au système \[ \begin{cases} a^2-b^2= & -3 \\ 2ab =& 4 \end{cases} \] La deuxième équation implique que \(a\) et \(b\) sont non-nuls et donc \(b=\frac{2}{a}\). En insérant dans la première équation on obtient \[ a^2-\frac{4}{a^2}=-3 \,\Leftrightarrow\,a^4 + 3a^2 -4 = 0 \, \Leftrightarrow \, a^2\in \{1,-4\} \] Puisque \(a\in\mathbb{R}\), seulement la première solution est possible; on a donc \(a=+1\) (et dans ce cas \(b=+2\)) ou alors \(a=-1\) (et dans ce cas \(b=-2\)). Ainsi les solutions de l'équation initiale sont \(z_{1}=1+2\mathsf{i}\) et \(z_{2}=-1-2\mathsf{i}\) (ce qui est bien sur la figure du dessus).
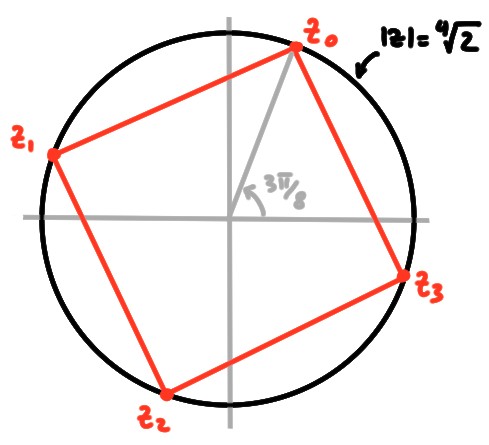
3. Puisque \(\omega=-2\mathsf{i}=2e^{\mathsf{i} \frac{3\pi}{2}}\), on a \[ z_k=\sqrt[4]{2}e^{\mathsf{i}(\frac{3\pi}{8}+\frac{\pi}{2}k)}\quad k\in \{0,1,2,3\}\,.\] Ces racines sont situées sur les sommets d'un carré:
   
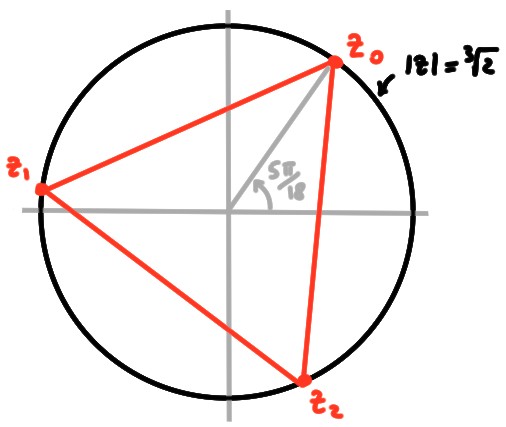
4. Comme \[\omega=-\sqrt{3}+\mathsf{i}=2(-\tfrac{\sqrt{3}}{2}+\tfrac{\mathsf{i}}{2})= 2e^{\mathsf{i}(\frac{5\pi}{6})}\,,\] les racines sont \[z_k=\sqrt[3]{2}\,e^{\mathsf{i}(\frac{5\pi}{18}+\frac{2\pi}{3}k)}\,,\quad k\in \{0,1,2\}\,.\] En remarquant que \(\frac{5\pi}{18}\) correspond à un angle de \(50^{\circ}\),