Dans chacun des cas ci-dessous, nous donnerons toujours l'exemple aussi simple que possibe de fonction qui satisfait à cette propriété.
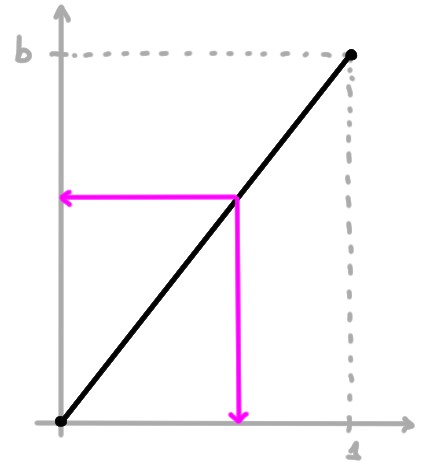
- On peut prendre la fonction dont le graphe est le segment reliant
\((0,0)\) à \((1,b)\) (sans ses extrémités):
\[\begin{aligned}
f:]0,1[&\to]0,b[\\
x&\mapsto f(x)=bx
\end{aligned}\]
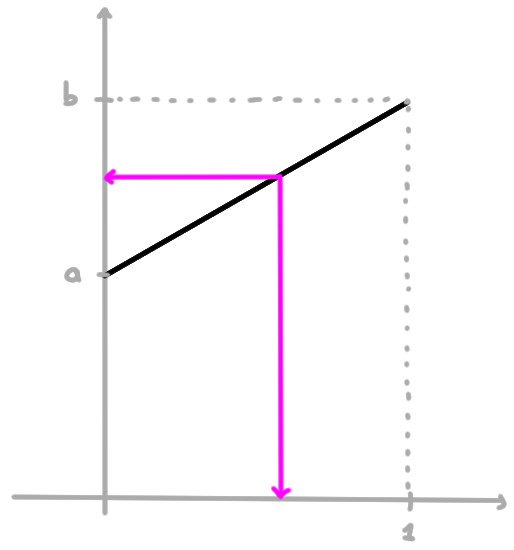
- On peut prendre la fonction dont le graphe est le segment reliant
\((0,a)\) à \((1,b)\) (sans ses extrémités):
\[\begin{aligned}
f:]0,1[&\to]a,b[\\
x&\mapsto f(x)=a+(b-a)x
\end{aligned}\]
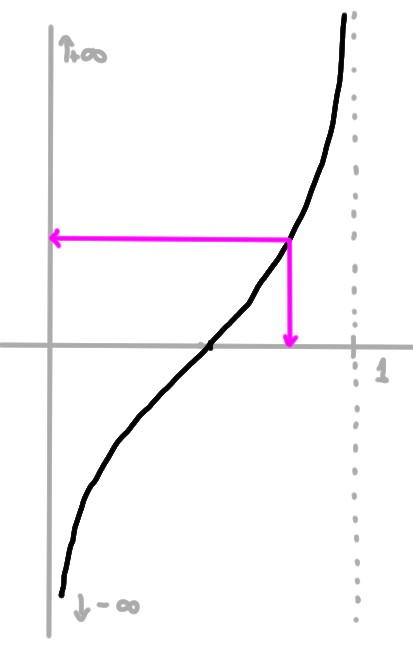
- On peut prendre par exemple
\[\begin{aligned}
f:]0,1[&\to]0,+\infty[\\
x&\mapsto f(x)=\tan(\tfrac{\pi}{2}x)
\end{aligned}\]
L'idée est qu'on connait le graphe de la fonction \(\tan:]-\frac{\pi}{2},\frac{\pi}{2}[\to \mathbb{R}\) (voir ici), donc aussi sur \(]0,\frac{\pi}{2}[\). On adapte ensuite pour passer de \(]0,\frac{\pi}{2}[\) à \(]0,1[\).

- Par exemple,
\[\begin{aligned}
f:]0,1[&\to\mathbb{R}\\
x&\mapsto f(x)=\tan(\pi(x-\tfrac12))
\end{aligned}\]
Ici aussi, on part du graphe de \(\tan:]-\frac{\pi}{2},\frac{\pi}{2}[\to\mathbb{R}\), qui est déjà une bijection, et on l'adapte pour se ramener à \(]0,1[\).
- (Rappel: cette partie de l'exercice est facultative!)
Suggestion: commencer par poser \(f(x)=x\), puis la modifier de manière à ce que \(f:]0,1[\to [0,1]\) devienne bijective (en particulier: \(0\) et \(1\in [0,1]\) doivent posséder au moins un antécédent). Une possibilité est de modifier \(f(x)=x\) seulement sur les points de la forme \(x=\frac1n\), comme suit: \[ f(x):= \begin{cases} 0&\text{ si }x=\tfrac12\,,\\ \frac{1}{n-2} & \text{ si }x=\tfrac1n\text{ avec }n\geqslant 3\,,\\ x&\text{ sinon}. \end{cases} \] Remarque: Cette fonction n'est pas continue. Comme on verra plus tard, une surjection \(f:]0,1[\to [0,1]\) ne peut pas être continue.
On pourra regarder l'approche semblable présentée sur la vidéo de Michael Penn.