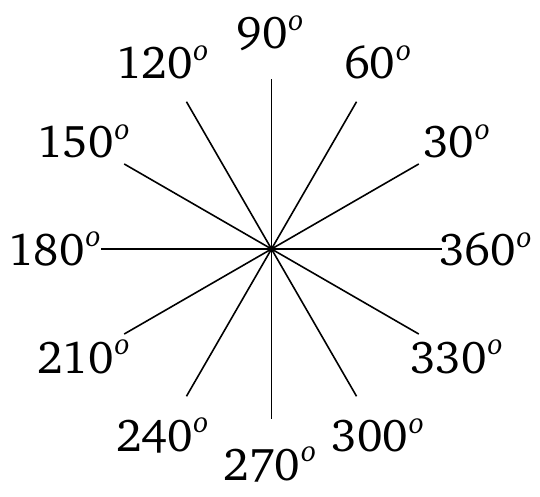
La mesure en degrés consiste à associer à l'angle total une mesure de \(360\) degrés, les autres angles étant mesurés de façon proportionnelle:
On rappelle ici les définitions et propriétés des
principales fonctions trigonométriques.
Pour commencer, rappelons
d'abord comment sont mesurés les angles dans le plan.
La mesure des angles se fait par un choix d'unités, et ce choix est déterminé une fois que l'on fixe la valeur de la mesure de l'angle total (ouverture correspondant à ''un tour complet'').
La mesure en degrés consiste à associer à l'angle total une mesure de \(360\) degrés, les autres angles étant mesurés de façon proportionnelle:

La mesure en radians est plus naturelle d'un point de vue géométrique, puisqu'elle consiste à mesurer une longueur le long d'un arc de cercle. Si la longueur parcourue est égale au rayon, ceci définit un angle de un radian:
L'angle total correspond donc à la longueur de la circonférence d'un cercle de rayon \(1\), à savoir \(2\pi\). Quelques angles intermédiaires:
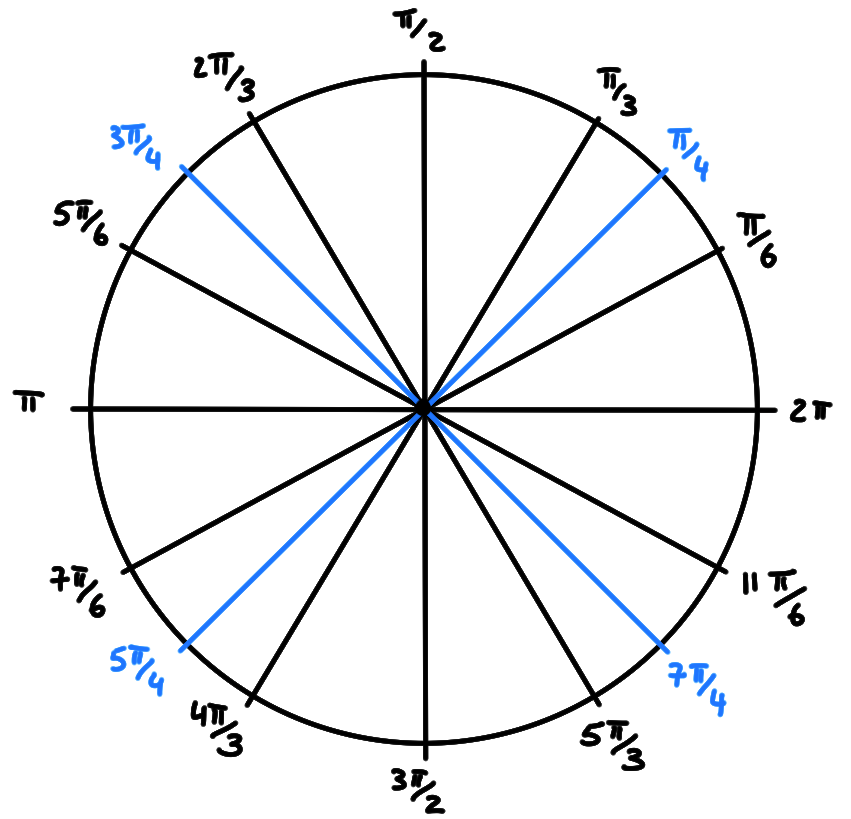
Soit un angle donné, dont la mesure en degrés est \(\alpha_d\) et celle en radians est \(\alpha_r\). Puisque \[ \frac{\alpha_d}{360}=\frac{\alpha_r}{2\pi}\,, \] on a la formule de conversion: \[ \alpha_d=\frac{180}{\pi}\alpha_r\,. \]
Donnons en passant l'expression de l'aire \(A\) d'un secteur circulaire de rayon \(r\), dont l'ouverture est un angle de \(\theta\) radians:
Dans le cas où l'angle est total \(\theta=2\pi\), ce secteur est un disque, et donc son aire est égale à \(\pi r^2\). Or pour un secteur quelconque, la proportionnalité existant entre l'angle \(\theta\) et l'angle total doit être la même que la proportionnalité existant entre l'aire \(A\) du secteur et celle du disque: \[ \frac{\theta}{2\pi}=\frac{A}{\pi r^2}\,. \] On a donc \[ \boxed{ A=\tfrac12 r^2\theta } \]
Considérons un triangle rectangle, et distinguons un de ses angles non droit, que l'on notera \(\alpha\):
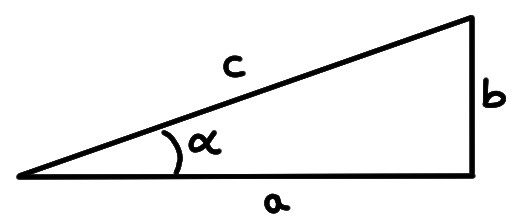
Le côté \(a\) est le cathète adjacent à \(\alpha\), le côté \(b\) est le cathète opposé à \(\alpha\), et \(c\) est l'hypothénuse.
Pour l'instant, \(\alpha\in ]0,\frac{\pi}{2}[\). On associe trois nombres à \(\alpha\), représentant chacun un rapport entre une paire de côtés:
Remarquons que l'on a toujours \[\tan(\alpha)=\frac{b}{a}=\frac{b/c}{a/c} =\frac{\sin(\alpha)}{\cos(\alpha)}\,. \]
Il est important de souligner que les nombres \(\sin(\alpha)\), \(\cos(\alpha)\), \(\tan(\alpha)\) sont définis comme étant des proportions dans le rectangle considéré; ils ne dépendant donc pas du choix particulier fait pour le rectangle. N'importe quel autre triangle semblable peut être utilisé:
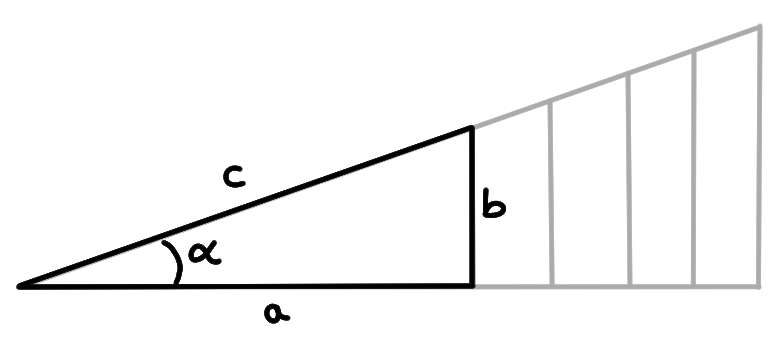
Si les nombres \(\sin(\alpha), \cos(\alpha),\tan(\alpha)\) sont géométriquement
bien définis,
il est en général difficile de les calculer exactement.
Il existe pourtant certains angles, appelés remarquables, qui sont des
parties rationnelles de \(2\pi\), pour lesquels
ces nombres peuvent être calculés exactement.
Commençons par les plus simples.
Considérons \(\alpha=\frac{\pi}{4}\), que l'on peut représenter dans un triangle rectangle dont les deux cathètes sont de longueurs \(1\), ce qui implique que son hypothénuse a pour longueur \(\sqrt{1^2+1^2}=\sqrt{2}\):
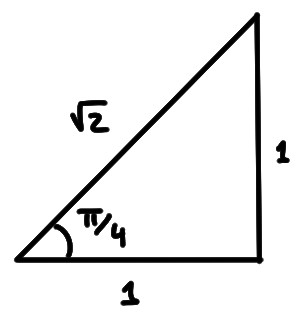
On a donc directement: \[\begin{aligned} \sin(\tfrac{\pi}{4})&=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}\\ \cos(\tfrac{\pi}{4})&=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}\\ \tan(\tfrac{\pi}{4})&=\frac{1}{1}=1\,. \end{aligned}\]
Considérons ensuite \(\alpha=\frac{\pi}{3}\), que l'on peut représenter comme un triangle rectangle égale à une moitié d'un triangle équilatéral de côté \(1\) (dont les trois angles sont égaux à \(\frac{\pi}{3}\)):
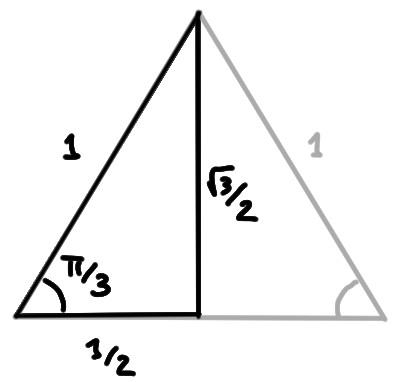
Par Pythagore, le cathète opposé a longueur \(l=\sqrt{1^2-(\frac12)^2}=\frac{\sqrt{3}}{2}\). On en déduit: \[\begin{aligned} \sin(\tfrac{\pi}{3})&=\frac{\sqrt{3}/2}{1}=\frac{\sqrt{3}}{2}\\ \cos(\tfrac{\pi}{3})&=\frac{1/2}{1}=\frac{1}{2}\\ \tan(\tfrac{\pi}{3})&=\frac{\sqrt{3}/2}{1/2}=\sqrt{3}\,. \end{aligned}\] Remarquons que l'autre angle non-droit de ce triangle vaut \(\frac{\pi}{6}\), et donc on a aussi \[\begin{aligned} \sin(\tfrac{\pi}{6})&=\frac{1/2}{1}=\frac{1}{2}\\ \cos(\tfrac{\pi}{6})&=\frac{\sqrt{3}/2}{1}=\frac{\sqrt{3}}{2}\\ \tan(\tfrac{\pi}{6})&=\frac{1/2}{\sqrt{3}/2}=\frac{1}{\sqrt{3}}\,. \end{aligned}\]
Nous l'avons dit plus haut, ce qui définit les fonctions trigonométriques sont
des proportions (ici: des quotients de longueurs);
elles ne dépendent pas du
triangle utilisé pour les définir. On peut donc choisir de
toujours les définir à partir d'un triangle dont l'hypothénuse est de longueur
égale à \(1\).
Or un triangle dont l'hypothénuse est de longueur \(1\) peut être placé dans le
plan cartésien, avec l'angle à l'origine,
le cathète adjacent le long de l'axe \(Ox\).
Son sommet , noté \(P\) sur l'image ci-dessous, est donc placé
sur le cercle de rayon \(1\)
centré à l'origine, appelé cercle trigonométrique.
Les trois nombres \(\sin(\alpha)\), \(\cos(\alpha)\) et \(\tan(\alpha)\) peuvent
alors être vus comme des longueurs (sur l'animation, faire varier
\(\alpha\) en déplaçant \(P\)):
L'utilisation du cercle trigonométrique permet de généraliser naturellement ces fonctions, en les définissant pour un angle quelconque \(\alpha\in\mathbb{R}\) (à part la tangente, définie pour tout angle qui n'est pas de la forme \(\frac{\pi}{2}+k\pi\), \(k\in \mathbb{Z}\)).
Graphe de la fonction \(\sin:\mathbb{R}\to [-1,1]\):
Graphe de la fonction \(\cos:\mathbb{R}\to [-1,1]\):
Graphe de la fonction \(\tan:\mathbb{R}\setminus \{\frac{\pi}{2}+k\pi,k\in\mathbb{Z}\}\to \mathbb{R}\):
La définition géométrique des fonctions trigonométriques (sur le cercle trigonométrique) permet d'obtenir facilement leurs principales propriétés élémentaires.
Par exemple, sous la transformation \(\alpha\mapsto \alpha+2\pi\), ces fonctions sont inchangées: \[ \sin(\alpha+2\pi)=\sin(\alpha)\,,\qquad \cos(\alpha+2\pi)=\cos(\alpha)\,. \] On a par contre que \[ \tan(\alpha+\pi)=\tan(\alpha)\,,\qquad \] on dit que la tangente est périodique, de période \(\pi\).
Ensuite, sous la transformation \(\alpha\mapsto \alpha+\pi\), \[\begin{aligned} \sin(\alpha+\pi)&=-\sin(\alpha)\\ \cos(\alpha+\pi)&=-\cos(\alpha)\\ \tan(\alpha+\pi)&=\tan(\alpha)\,, \end{aligned}\] et sous \(\alpha\mapsto \alpha+\frac{\pi}{2}\), \[\begin{aligned} \sin(\alpha+\tfrac{\pi}{2})&=\cos(\alpha)\\ \cos(\alpha+\tfrac{\pi}{2})&=-\sin(\alpha)\\ \tan(\alpha+\tfrac{\pi}{2})&=\frac{-1}{\tan(\alpha)}\,. \end{aligned}\]
Sous la transformation \(\alpha\mapsto \frac{\pi}{2}-\alpha\): \[\begin{aligned} \sin(\tfrac{\pi}{2}-\alpha)&=\cos(\alpha)\\ \cos(\tfrac{\pi}{2}-\alpha)&=\sin(\alpha)\\ \tan(\tfrac{\pi}{2}-\alpha)&=\frac{1}{\tan(\alpha)}\,. \end{aligned}\] Enfin, \[\begin{aligned} \sin(-\alpha)&=-\sin(\alpha)\\ \cos(-\alpha)&=\cos(\alpha)\\ \tan(-\alpha)&=-\tan(\alpha) \end{aligned}\]
Par le Théorème de Pythagore (dans le cercle trigonométrique), on obtient l'identité fondamentale \[ \sin^2(\alpha)+\cos^2(\alpha)=1\,. \] Passons aux identités fondamentales concernant les sommes d'angles:
Théorème: Pour tous \(\alpha,\beta\in\mathbb{R}\), \[\begin{aligned} \sin(\alpha+\beta)&=\sin(\alpha)\cos(\beta)+\sin(\beta)\cos(\alpha)\\ \cos(\alpha+\beta)&=\cos(\alpha)\cos(\beta)-\sin(\alpha)\sin(\beta)\\ \tan(\alpha+\beta)&=\frac{\tan(\alpha)+\tan(\beta)}{ 1-\tan(\alpha)\tan(\beta)}\,. \end{aligned}\]
Pour simplifier, supposons que \(0\lt \alpha,\beta\lt \frac{\pi}{4}\), et plaçons l'angle \(\alpha+\beta\) sur le cercle trigonométrique:
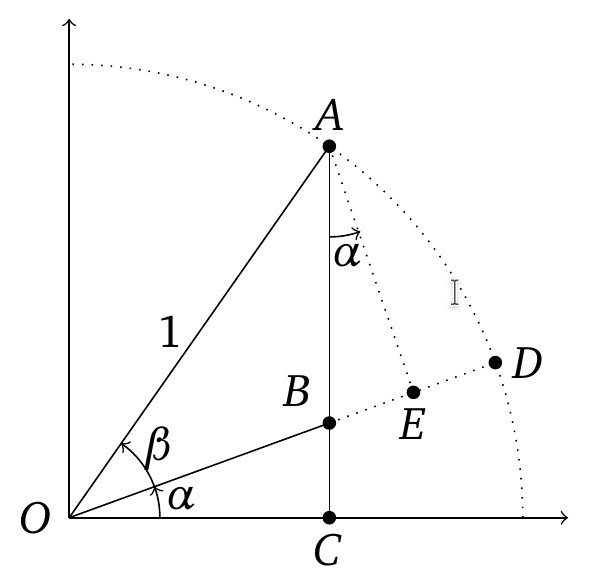
Comme conséquence, des formules très utiles dans la pratique:
Les formules ci-dessus permettent de trouver des formules exactes pour des angles plus compliqués que les quelques angles remarquables mentionnés plus haut. En effet, si on sait par exemple que \(\cos(\frac{\alpha}{2})\geqslant 0\), et qu'on connaît \(\cos(\alpha)\), on peut utiliser la formule ci-dessus comme suit: \[ \cos(\tfrac{\alpha}{2})=+\sqrt{\frac{1+\cos(\alpha)}{2}}\,. \]
Exemple: Puisque \(0\lt \frac{\pi}{8}\lt \frac{\pi}{2}\), on a \(\cos(\frac{\pi}{8})\gt 0\), et donc en posant \(\alpha=\frac{\pi}{4}\), \[\begin{aligned} \cos(\tfrac{\pi}{8}) &=\cos(\tfrac{\alpha}{2})\\ &=\sqrt{\frac{1+\cos(\alpha)}{2}}\\ &=\sqrt{\frac{1+\tfrac{\sqrt{2}}{2}}{2}}\\ &=\frac{\sqrt{2+\sqrt{2}}}{2}\,, \end{aligned}\] et donc \[ \sin(\tfrac{\pi}{8})=+\sqrt{1-\cos^2(\tfrac{\pi}{8})}=\frac{\sqrt{2-\sqrt{2}}}{2}\,, \] \[ \tan(\tfrac{\pi}{8})=\frac{\sqrt{2-\sqrt{2}}}{\sqrt{2+\sqrt{2}}}\,. \]
L'exemple ci-dessus montre que l'on peut, a priori, calculer les valeurs exactes des fonctions trigonométriques pour tous les angles de la forme \(\frac{\pi}{2^n}\).
Montrons la première identité. En utilisant la formule du dessus, on développe les termes du membre de droite, \[\begin{aligned} \sin\bigl(\frac{x+y}{2}\bigr) &=\sin(\tfrac{x}{2})\cos(\tfrac{y}{2}) +\cos(\tfrac{x}{2})\sin(\tfrac{y}{2})\\ \cos\bigl(\frac{x-y}{2}\bigr) &=\cos(\tfrac{x}{2})\cos(\tfrac{y}{2})-\sin(\tfrac{x}{2})\sin(-\tfrac{y}{2})\\ &=\cos(\tfrac{x}{2})\cos(\tfrac{y}{2})+\sin(\tfrac{x}{2})\sin(\tfrac{y}{2})\,. \end{aligned}\] En multipliant ces deux lignes, une simplification mène à \[\begin{aligned} \sin\bigl(\frac{x+y}{2}\bigr)\cos\bigl(\frac{x-y}{2}\bigr) &= \sin\bigl(\tfrac{x}{2}\bigr)\cos\bigl(\tfrac{x}{2}\bigr) + \sin\bigl(\tfrac{y}{2}\bigr)\cos\bigl(\tfrac{y}{2}\bigr)\\ &=\tfrac12\sin(x)+\tfrac12\sin(y)\,. \end{aligned}\]