Soit \(f:\mathbb{R}\to \mathbb{R}\) définie par
\[f(x)=\frac{2x}{x^2+25}\,.\]
Calculer \(\mathrm{Im} (f)\). Ensuite, déterminer le nombre
de préimages pour chaque \(y\in \mathrm{Im} (f)\).
Il s'agit ici de travailler par calcul uniquement.
Pour un rappel de la définition générale
de l'
ensemble image d'une fonction
\(f:A\to B\), voir
ici.
Pour son calcul dans le cas des fonctions réelles, voir
ici.
On trouve l'ensemble image en trouvant les \(y\in\mathbb{R}\) pour lesquels...
... il existe au moins un \(x\) tel que \(y=f(x)\).
Ici, cela signifie que
\[
y=\frac{2x}{x^2+25}\,.
\]
Savoir si cette équation possède une solution en \(x\) revient à résoudre une
équation du deuxième degré en \(x\),
où \(y\) joue le rôle de paramètre.
On fera attention à distinguer le rôle spécial joué par la valeur \(y=0\).
On pourra, dans la solution, faire usage de la fonction racine carrée.
Il s'agit de trouver les \(y\in \mathbb{R}\) (l'ensemble d'arrivée)
pour lesquels il existe au moins un
\(x\in \mathbb{R}\) (l'ensemble de départ) tel que \(f(x)=y\).
Ceci correspond à résoudre l'équation du deuxième degré en \(x\):
\[yx^2-2x+25y=0\,.\]
(On a pu multiplier par \(x^2+25\) puisque c'est une quantité qui ne s'annule
pour aucune valeur de \(x\).)
- Si \(y=0\), cette équation est du premier degré en \(x\) et
a pour solution \(x=0\).
Donc \(y=0\) appartient à l'ensemble image de \(f\).
- Si \(y\neq 0\), l'équation est du deuxième degré, et ses
solutions sont
\[x=\frac{1\pm\sqrt{1-25y^2}}{y}\,,\]
qui sont bien définies seulement si
\(|y|\leqslant\frac15\).
Donc l'ensemble des \(y\) non nuls tels que \(|y|\leqslant 1/5\) font partie de
l'ensemble image.
Ainsi, \(\mathrm{Im} (f)=[-\tfrac15,\tfrac15]\). Remarquons que
\(-\frac15,0,+\frac15\) sont les uniques éléments
de \(\mathrm{Im} (f)\) qui possèdent exactement une préimage;
tous les autres possèdent exactement deux préimages.
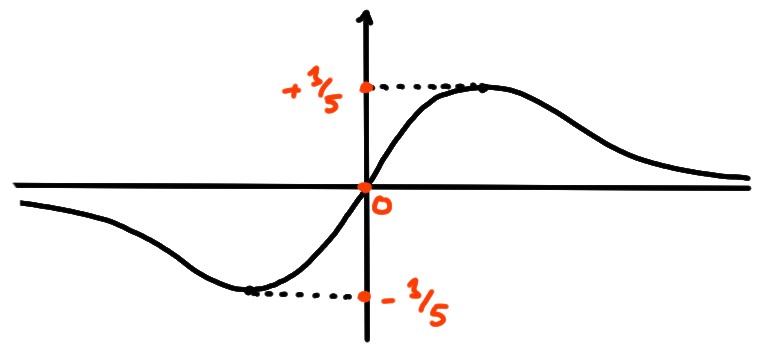
On comprend bien le résultat de cette analyse si on esquisse
le graphe de \(f\):
En effet, toute droite horizontale à hauteur
\(y\in [-1/5,+1/5]\) coupe le graphe de \(f\) en au moins un point. Si \(y=0\)
ou \(\pm 1/5\), cette droite coupe le graphe en exactement un point; pour les
autres valeurs, elle le coupe en exactement deux points.