Considérons un objet de masse \(m\).
A un instant donné, on définit l'énergie cinétique de son CM par
\[ E_\text{cin,CM}=\frac{1}{2}mv_\text{CM}^2\,. \]C'est l'énergie associée au mouvement. Unité: \(\text{kg}\,\text{m}^2\,\text{s}^{-2} = \text{N}\,\text{m} = \text{J}\) (''joule'').
La variation d'énergie cinétique entre un instant \(t_1\) et un instant \(t_2\) est donnée par le théorème de l'énergie cinétique pour le CM:
\[ E_\text{cin,CM}(2)-E_\text{cin,CM}(1) =W^\text{ext}_{1\rightarrow 2}\,, \]où
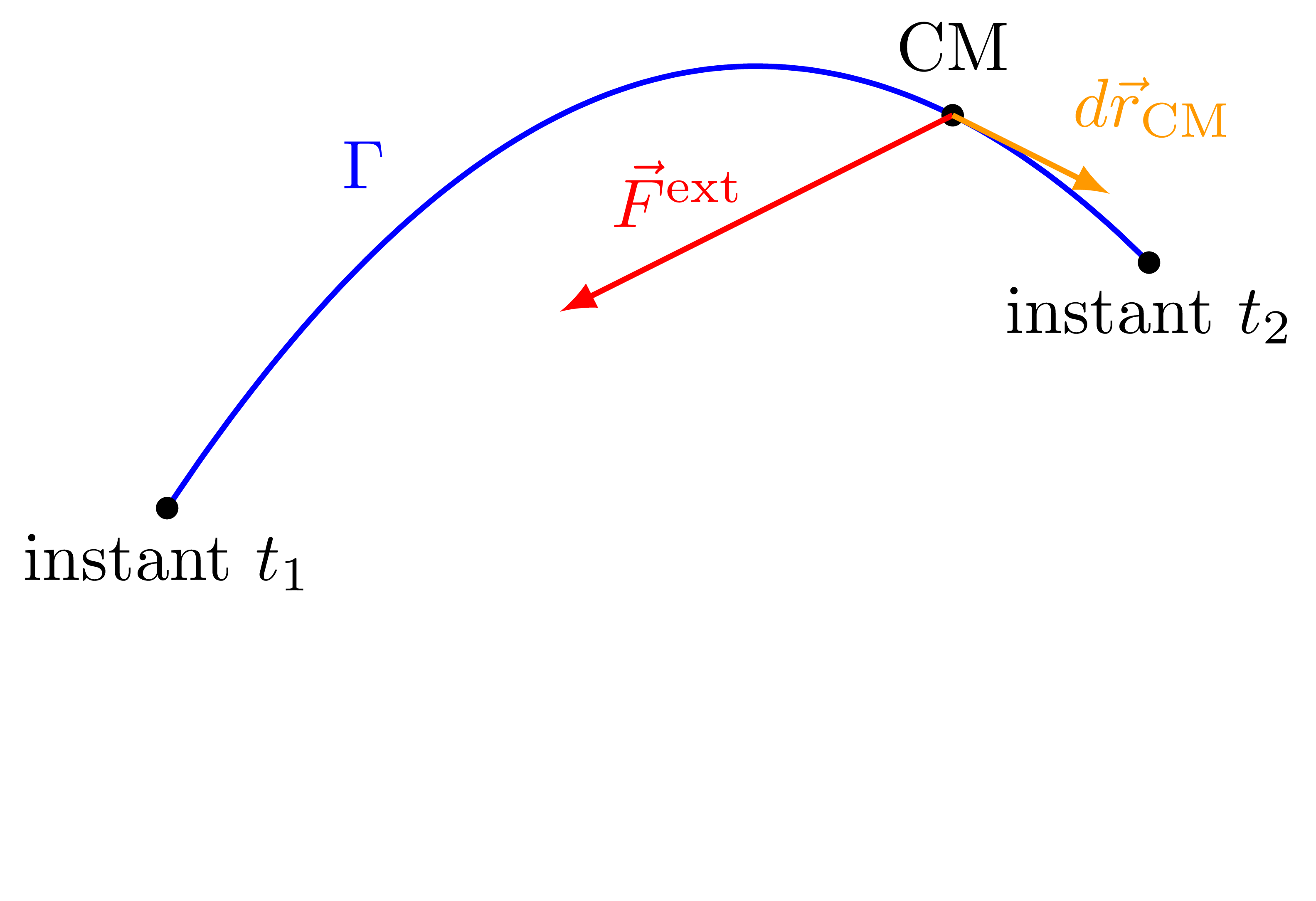
\[ \displaystyle W^\text{ext}_{1\rightarrow 2} =\int_{1}^{2}{dW^\text{ext}} =\int_{1}^{2} \vec{F}^\text{ext}\cdot d\vec{r}_\text{CM} \]est le travail des forces extérieures \(\vec{F}^\text{ext}\) sur le CM, \(dW^\text{ext}= \vec{F}^\text{ext}\cdot d\vec{r}_\text{CM}\) étant le ravail infinitésimal des forces extérieures sur le CM pour un déplacement \(d\vec{r}_\text{CM}\). Le symbole d'intégration \(\int\) désigne la somme des travaux infinitésimaux effectués entre \(1\) et \(2\).
Force conservative: Une force est dite conservative si son travail sur l'objet considéré ne dépend que des extrémités du chemin que l'objet parcourt, et non du chemin lui-même.
Energie potentielle: Le travail d'une force conservative entre un instant \(t_1\) et un instant \(t_2\) peut être écrit comme une différence d'énergie potentielle: \[W_{1\rightarrow 2}(\vec{F}_\text{cons}^{\text{ext}}) = E_\text{pot,CM}(1) - E_\text{pot,CM}(2)\,.\] L'énergie potentielle est associée à une position \(\vec{r}\) du CM de l'objet et est définie à une constante arbitraire près.
Exemples:
Energie mécanique: \[ E_\text{m\'{e}c,CM} = E_\text{cin,CM}+E_\text{pot,CM}\,. \] C'est l'énergie associée au mouvement et à la position du CM de l'objet.
La variation d'énergie mécanique entre un instant \(t_1\) et un instant \(t_2\) est donc donnée par
\[ E_\text{méc,CM}(2)-E_\text{méc,CM}(1) =W_{1\rightarrow 2} (\vec{F}_\text{non cons}^{\text{ext}})\,. \]En d'autres termes, si toutes les forces sont conservatives (ou ne travaillent pas), l'énergie mécanique du CM est conservée, \(E_\text{m\'{e}c,CM} =\text{cste}\).
Dernière compilation: 2025-03-16 (13:57:55)
Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)
