ICS CMS | R. Sauser (EPFL)

4.4 Recherche de zéros

La méthode de la bissection

SciPy fournit une fonction scipy.optimize.bisect qui implémente la méthode de la bissection et demande trois arguments obligatoires :

la fonction \(f(x)\),
une limite inférieure \(a\),
une limite supérieure \(b\).

Un paramètre optionnel xtol (par défaut 2e-12) précise l'erreur maximale tolérée.

Un autre paramètre optionnel, maxiter, permet d'interrompre la méthode après un certain nombre d'itérations (par défaut, 100).

Il est primordial que \(f(a)\) et \(f(b)\) n'aient pas le même signe (condition de Bolzano).


from scipy import optimize
def f(x):
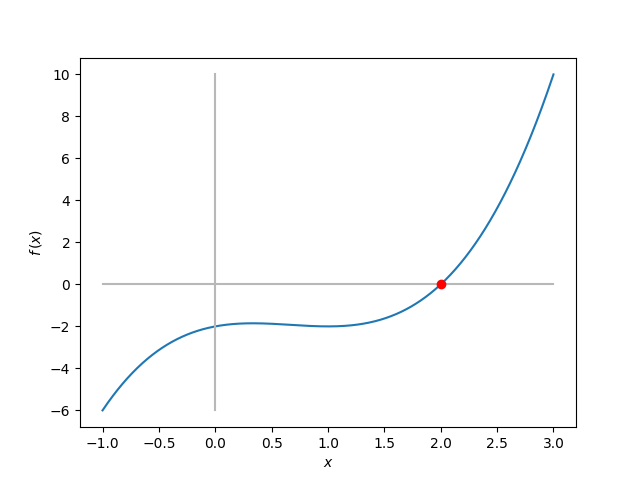
    return (1+x**2)*(x-2)
x = optimize.bisect(f,-0.5,2.5,xtol=1e-3,maxiter=100)
print("Le zéro trouvé par la méthode est x =", x)
print("L'erreur commise est donnée par 2-x =", 2-x)

import numpy as np
import matplotlib.pyplot as plt
x_vec = np.linspace(-1,3,1000)
y_vec = f(x_vec)
plt.xlabel('$x$')
plt.ylabel('$f\,(x)$')
plt.plot(x_vec,y_vec)
plt.plot([x_vec[0],x_vec[-1]], [0,0], c='0.72')
plt.plot([0,0], [y_vec.min(),y_vec.max()], c='0.72')
plt.plot(x,f(x),'ro')
plt.show()


Le zéro trouvé par la méthode est x = 1.999755859375
L'erreur commise est donnée par 2-x = 0.000244140625

La fonction `newton`

SciPy fournit la fonction scipy.optimize.newton qui implémente la méthode de Newton (ou la méthode de la sécante, ou la méthode de Halley) et demande deux arguments obligatoires :

la fonction \(f(x)\);
un \(x_0\) proche du zéro cherché.

La dérivée de \(f\) peut être fournie de manière optionnelle (argument fprime). En son absence, la méthode de la sécante est utilisée. On retrouve les paramètres optionnels liés à la tolérance, tol (par défaut, 1.48e-08), et au nombre maximum d'itérations, maxiter (par défaut, 50).

Lorsque les première et deuxième dérivées sont fournies (via fprime et fprime2), la méthode utilisée est celle de Halley. Remarquons que nous n'avons pas discuté cette méthode dans le chapitre 3. Elle a été proposée par l'astronome Edmond Halley et généralise la méthode de Newton. Sa convergence est cubique.

Exemple d'utilisation avec la fonction \(f(x)=(1+x^2)(x-2)\) :

a) Méthode de la sécante (la dérivée n'est pas fournie à la fonction newton)


from scipy import optimize
def f(x):
    return (1+x**2)*(x-2)
x = optimize.newton(f,1.5,full_output=True)
print('Méthode de la sécante : \n',x)


Méthode de la sécante : 
 (1.9999999999999991,       converged: True
           flag: 'converged'
 function_calls: 9
     iterations: 8
           root: 1.9999999999999991)

b) Méthode de Newton (la première dérivée est fournie à la fonction newton)


from scipy import optimize
def f(x):
    return (1+x**2)*(x-2)
def f_prime(x):
    return 3*x**2-4*x+1
x = optimize.newton(f,1.5,fprime=f_prime,full_output=True)
print('Méthode de Newton : \n',x)


Méthode de Newton : 
 (2.0,       converged: True
           flag: 'converged'
 function_calls: 12
     iterations: 6
           root: 2.0)

c) Méthode de Halley (les deux premières dérivées sont fournies à la fonction newton)


from scipy import optimize
def f(x):
    return (1+x**2)*(x-2)
def f_prime(x):
    return 3*x**2-4*x+1
def f_seconde(x):
    return 6*x-4
x = optimize.newton(f,1.5,fprime=f_prime,fprime2=f_seconde, full_output=True)
print('Méthode de Halley : \n',x)


Méthode de Halley : 
 (2.0,       converged: True
           flag: 'converged'
 function_calls: 13
     iterations: 4
           root: 2.0)

La fonction `fsolve`

SciPy permet également de faire appel à un algorithme a priori plus efficace pour trouver un zéro d'une fonction à l'aide de la fonction scipy.optimize.fsolve. La méthode ne nécessite qu'un point de départ (proche du point cherché). Elle ne fournit pas de garantie de convergence. Si la dérivée de la fonction n'est pas fournie en argument, elle est estimée.

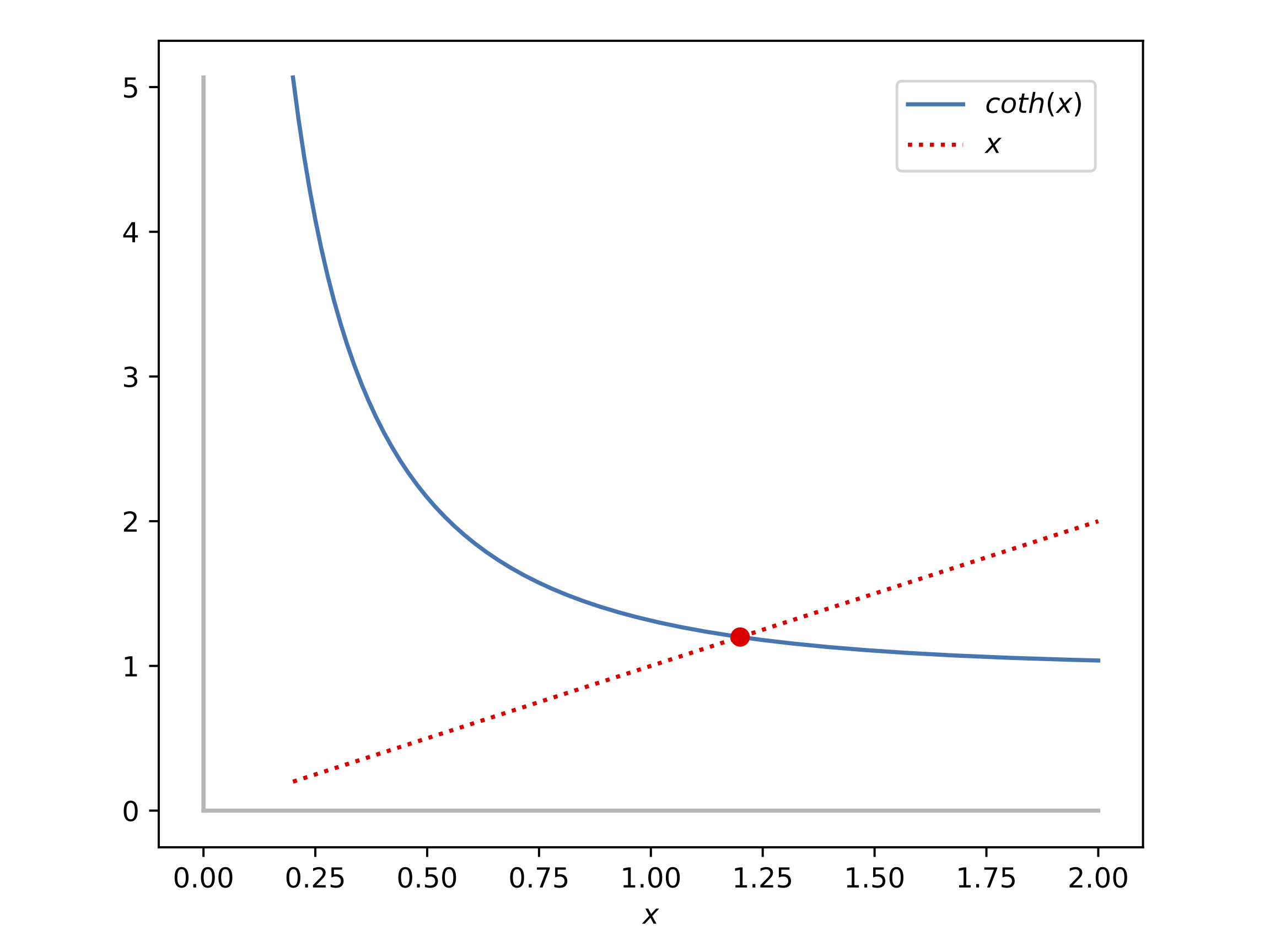
Recherchons par exemple la solution de l'équation \(\coth{(x)}=x\) pour \(x>0\) :


import numpy as np
from scipy import optimize
def f(x):
    return np.cosh(x)/np.sinh(x) - x
zero = optimize.fsolve(f,1.0)
print('x = ', zero[0], ' et f(x) = ', f(zero[0]))


x =  1.1996786402577135  et f(x) =  2.90878432451791e-14

Remarquons que la fonction fsolve permet de résoudre des problèmes multidimensionnels, c'est-à-dire des problèmes dans lesquels plusieurs inconnues scalaires sont à déterminer (la dimension d'un problème est donnée par le nombre de variables scalaires dont on cherche à déterminer les valeurs). Ainsi, l'exemple suivant correspond à un système bidimensionnel (intersection d'une ellipse et d'une parabole) :

\[ \left\{\begin{matrix} \displaystyle\frac{x^2}{8} + \frac{y^2}{2} &=& 1 & \text{(ellipse)}\\ \displaystyle y &=& \displaystyle \frac{x^2}{4} & \text{(parabole)} \end{matrix}\right. \]


import numpy as np
from scipy import optimize
def fct(valeurs):
    x = valeurs[0]    
    y = valeurs[1]
    SE = np.zeros(2, float) # SE : Système d'Equations (ndarray)
    SE[0] = pow(x,2)/8 + pow(y,2)/2 - 1    
    SE[1] = y - pow(x,2)/4
    return SE
valeurs_0 = np.array([0.5,0.5])
solution = optimize.fsolve(fct,valeurs_0)
print('x = ',solution[0],' et  y = ',solution[1])


x =  2.0000000000000018  et  y =  1.0000000000000007

4.4 Recherche de zéros

La méthode de la bissection

La fonction newton

La fonction fsolve

La fonction `newton`

La fonction `fsolve`