ICS CMS | R. Sauser (EPFL)

4.3 Ajustement de courbes (de paramètres)

La fonction scipy.optimize.curve_fit permet un ajustement optimal du (ou des) paramètre(s) d'une fonction que l'on pense susceptible de décrire un ensemble de données expérimentales.

Par exemple, essayons d'ajuster une fonction polynomiale \(f(t)=at^b+c\), où \(a\), \(b\) et \(c\) sont des paramètres réels inconnus, aux données collectées lors de la chute libre d'une masse (voir le fichier ChuteLibreData.txt déjà utilisé dans ce cours).

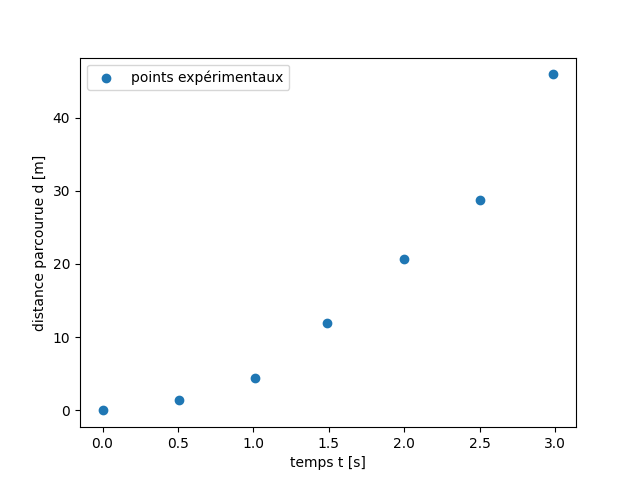
Représentation des points expérimentaux :


import numpy as np
import matplotlib.pyplot as plt
from scipy import optimize
t,d = np.loadtxt('ChuteLibreData.txt', usecols = (1,2), skiprows = 4, unpack = True)
plt.xlabel("temps t [s]")
plt.ylabel("distance parcourue d [m]")
plt.scatter(t,d,label='points expérimentaux')
plt.legend(loc='best')
plt.show()

La fonction plt.scatter() permet de représenter uniquement les points, sans les relier.

Ajustement des paramètres d'une fonction polynomiale aux données expérimentales :


def fct_fit(x,a,b,c):
    return a * x**b + c
parametres, m_covariance = optimize.curve_fit(fct_fit,t,d)
print('tableau des paramètres : ', parametres)
print('matrice (tableau) de covariance : \n', m_covariance)


tableau des paramètres :  [4.67235125 2.06247522 0.19456514]
matrice (tableau) de covariance : 
 [[ 0.92275613 -0.1731547  -0.81855416]
 [-0.1731547   0.03352579  0.13967152]
 [-0.81855416  0.13967152  1.22872764]]

Les valeurs estimées des paramètres obtenues grâce à la fonction scipy.optimize.curve_fit sont : \(a\cong 4.766\), \(b\cong 2.020\) et \(c\cong 0.095\).

Les valeurs théoriques attendues sont évidemment (chute libre à la surface de la Terre) : \(a = \displaystyle\frac{1}{2}g \cong 4.903\), \(b=2\) et \(c=0\).

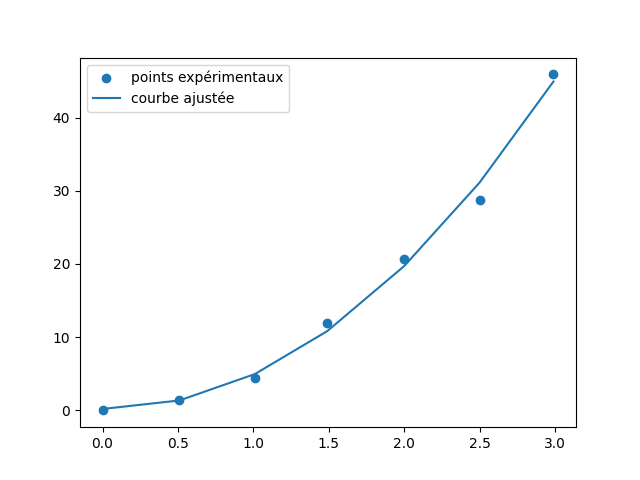
Représentation des points expérimentaux et de la courbe ajustée :


plt.scatter(t,d,label='points expérimentaux')
plt.plot(t, fct_fit(t, parametres[0], parametres[1], parametres[2]), label='courbe ajustée')
plt.legend(loc='best')
plt.show()