ICS CMS | R. Sauser (EPFL)

8.1 Intégration numérique

La bibliothèque SciPy, à travers le module scipy.integrate, fournit plusieurs routines d'intégration parmi lesquelles certaines portent des noms qui nous sont désormais familiers. On peut citer en particulier les méthodes trapezoid (formule du trapèze) et simpson (formule de Simpson). Mentionnons également la fonction quad qui permet de calculer très facilement et très efficacement une intégrale définie du type :

\[ I = \int_{a}^{b}{f(x)dx}\,. \]

Selon la documentation, la routine quad utilise la bibliothèque QUADPACK. Elle admet pour arguments la fonction \(f(x)\) à intégrer (l'intégrande), ainsi que les bornes inférieure et supérieure \(a\) et \(b\). Elle retourne deux valeurs sous la forme d'un tuple :

l'approximation numérique de l'intégrale ;
un majorant de l'erreur commise.

A titre d'exemple simple, nous allons reprendre l'exercice 3 de la Série 22 d'Analyse I et calculer l'aire du domaine (fini) limité par les courbes d'équation :

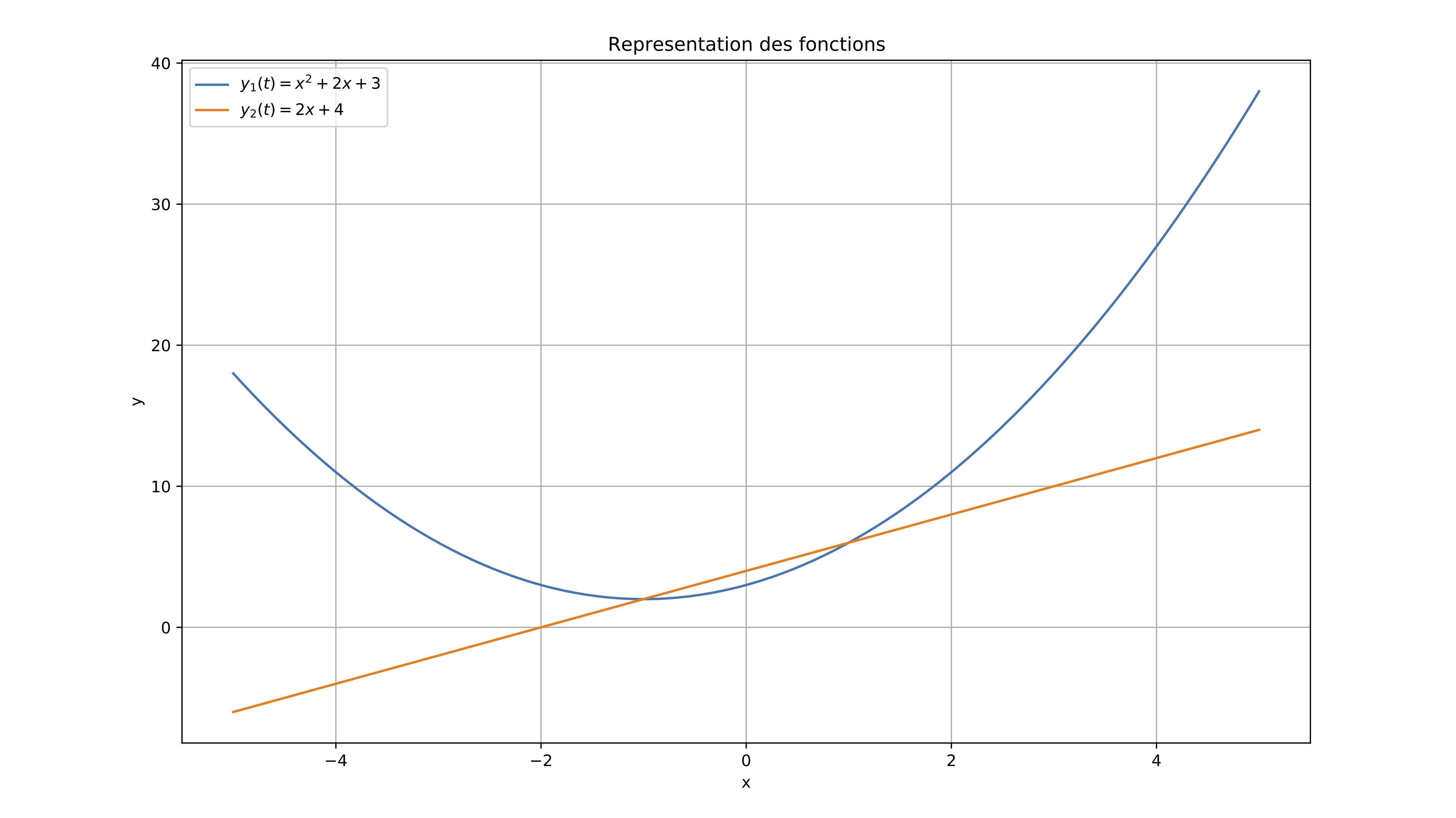
\[ y_1 = x^2 + 2x + 3~~\text{ et }~~y_2 = 2x + 4\,. \]

Il est aisé de représenter ces courbes pour localiser le domaine qui nous intéresse :


import numpy as np
import matplotlib.pyplot as plt
def y_1(x):
    return x**2 + 2*x + 3
def y_2(x):
    return 2*x + 4
x = np.linspace(-5,5,100)
plt.figure(figsize=(12,8)) 
plt.plot(x,y_1(x), label='$y_1(t) = x^2 + 2x + 3$')
plt.plot(x,y_2(x), label='$y_2(t) = 2x + 4$')
plt.grid()
plt.xlabel('x') ; plt.ylabel('y') ; plt.legend(loc='best')
plt.title('Représentation des fonctions')
plt.show()

Figure obtenue :

On peut déterminer les bornes \(a\) et \(b\) du domaine en définissant une fonction \(f(x)= y_2(x) - y_1(x)=-x^2+1\) et en recherchant ses zéros (par exemple, par la méthode de la bissection, de la sécante ou de Newton) :


from scipy import optimize
def f(x):
    return y_2(x) - y_1(x)
a = optimize.bisect(f, -4, 0)
b_1 = optimize.newton(f,2)
def f_prime(x):
    return -2*x
b_2 = optimize.newton(f,2,fprime=f_prime)
print(a, b_1, b_2)


-1.0 1.0000000000000002 1.0

On en déduit que \(a=-1\) et \(b=1\).

On peut alors préciser le domaine à considérer :


x = np.linspace(a,b_2,100)

plt.figure(figsize=(12,8)) 
plt.plot(x,y_1(x), label='$y_1(t) = x^2 + 2x + 3$')
plt.plot(x,y_2(x), label='$y_2(t) = 2x + 4$')

plt.fill_between(x, y_2(x), y_1(x), alpha=0.3)

plt.grid()
plt.plot([a],[y_1(a)],'ro')
plt.plot([b_2],[y_1(b_2)],'ro')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc='best')
plt.title('Représentation du domaine à étudier')
plt.show()

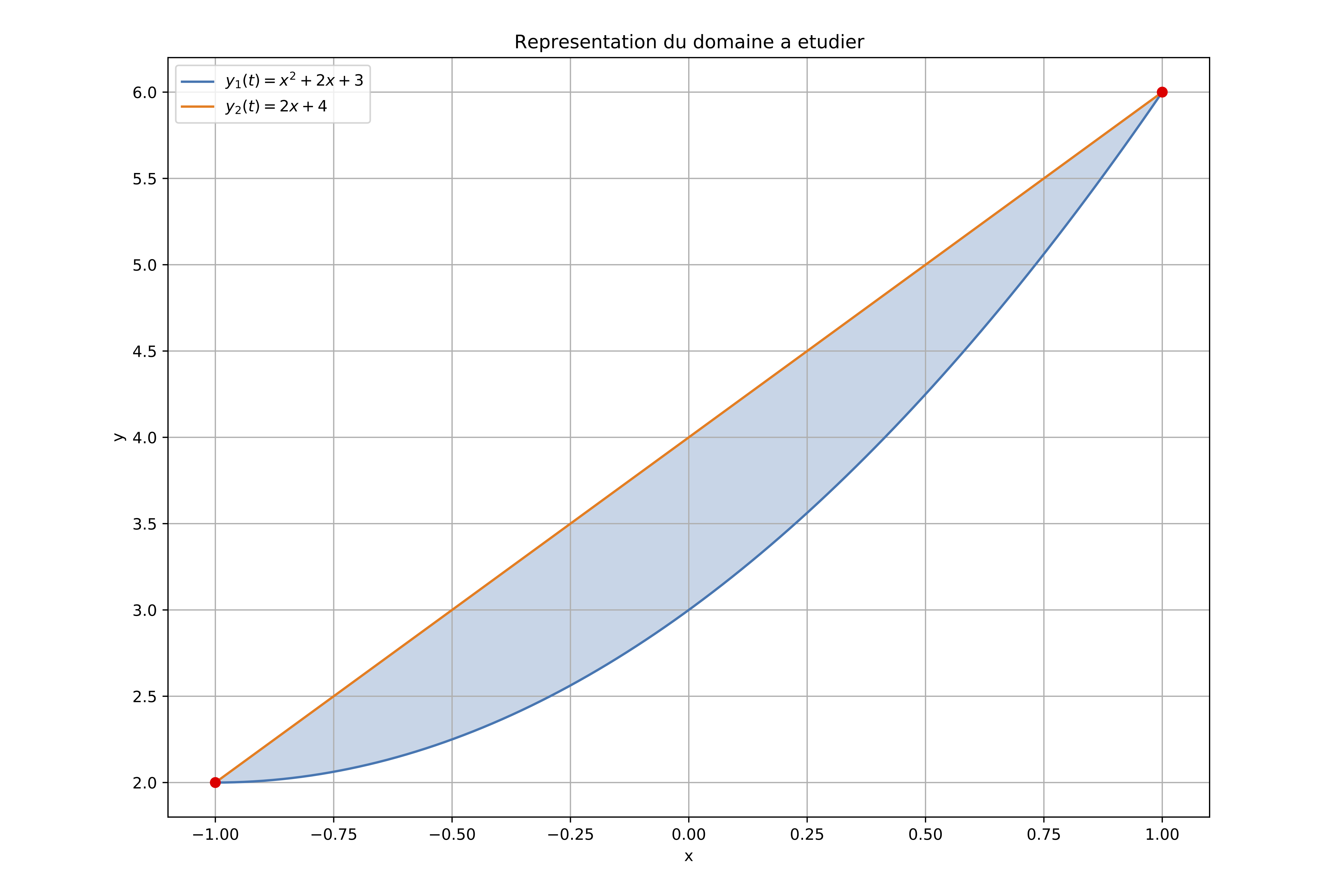
\(\ldots\,\) et intégrer :


from scipy import integrate
I, erreur = integrate.quad(f, a, b_2)
print(I, erreur)


1.3333333333333335 1.4802973661668755e-14

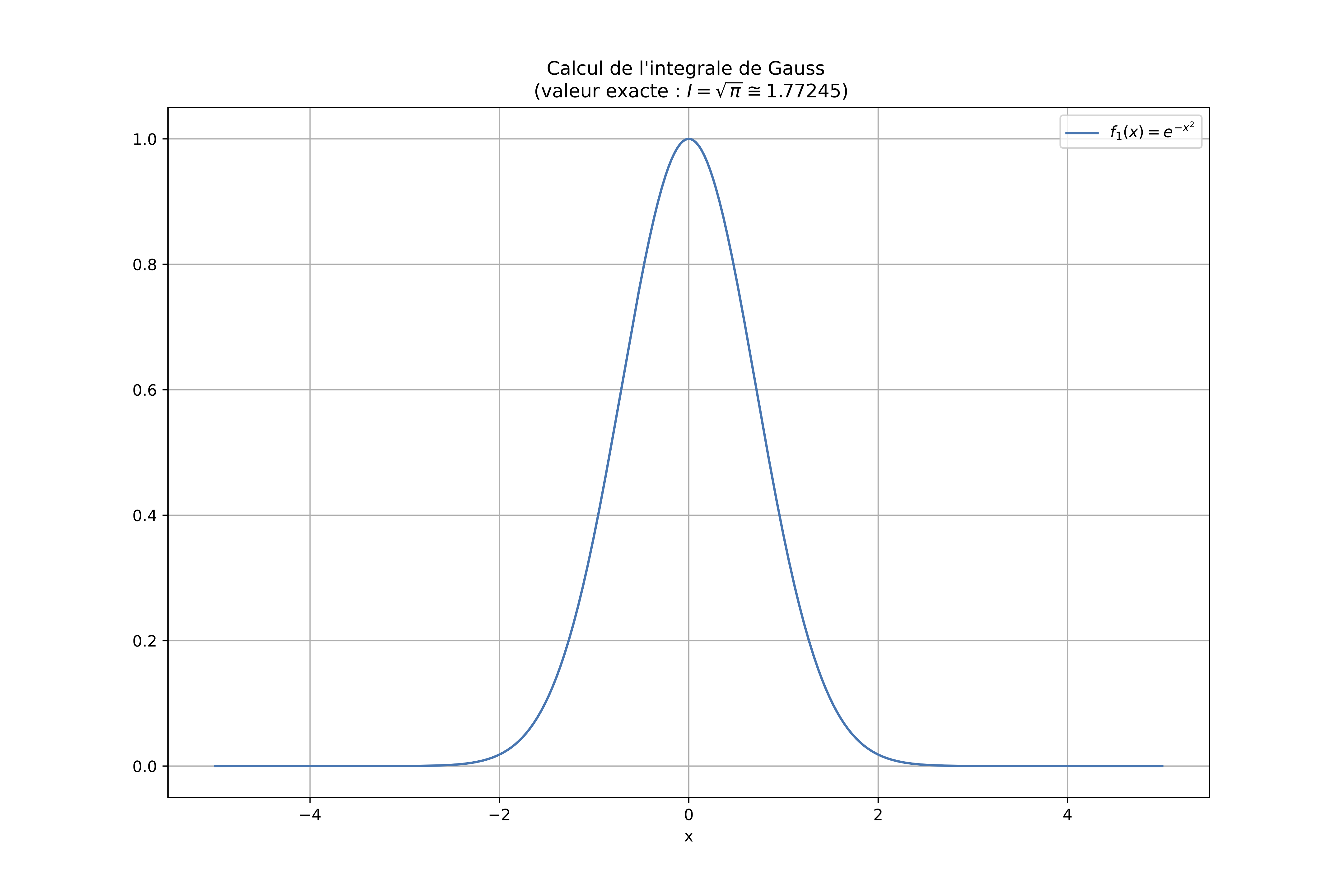
Remarquons que la fonction quad permet également d'effectuer des intégrations sur un intervalle non borné. Ainsi, il est par exemple possible d'obtenir une bonne approximation d'une intégrale de Gauss :

\[ I = \int_{-\infty}^{\infty}{e^{-x^2}dx}\,. \]


import numpy as np
import matplotlib.pyplot as plt
def f_1(x): return np.exp(-x**2)

x = np.linspace(-5,5,1000)
plt.figure(figsize=(12,8)) 
plt.plot(x,f_1(x), label='$f_1(x) = e^{-x^2}$')
plt.grid()
plt.xlabel('x') ; plt.legend(loc='best')
plt.title("Calcul de l'intégrale de Gauss \n (valeur exacte : $I=\sqrt{\pi}\cong 1.77245$)")
plt.show()

from scipy import integrate
I, erreur = integrate.quad(f_1, -np.inf, np.inf)
print(I, erreur)


1.7724538509055159 1.4202636780944923e-08

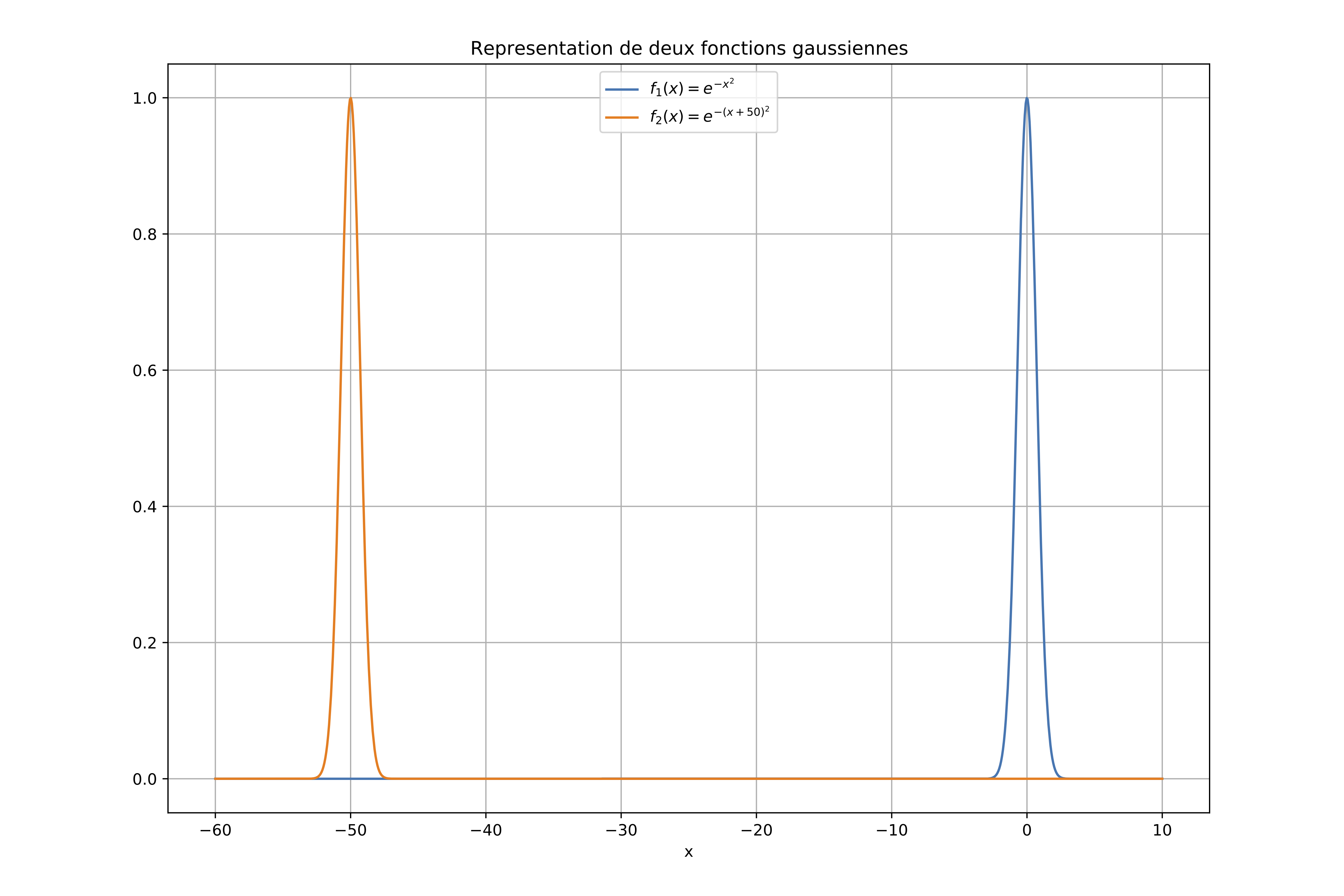
Comme le montrent les résultats ci-dessous, il convient toutefois d'utiliser une ''boîte noire'' numérique telle que la fonction quad avec tout l'esprit critique nécessaire :

\[ I = \int_{-\infty}^{\infty}{e^{-x^2}dx} = \int_{-\infty}^{\infty}{e^{-(x+50)^2}dx} = \sqrt{\pi}\,. \]


import numpy as np
import matplotlib.pyplot as plt
def f_1(x):
    return np.exp(-x**2)
def f_2(x):
    return np.exp(-(x+50)**2)

x = np.linspace(-60,10,1000)

plt.figure(figsize=(12,8)) 
plt.plot(x,f_1(x), label='$f_1(x) = e^{-x^2}$')
plt.plot(x,f_2(x), label='$f_2(x) = e^{-(x+50)^2}$')
plt.grid()
plt.xlabel('x') ; plt.legend(loc='best')
plt.title('Représentation de deux fonctions gaussiennes')
plt.show()

from scipy import integrate
I_1, erreur_1 = integrate.quad(f_1, -np.inf, np.inf)
I_2, erreur_2 = integrate.quad(f_2, -np.inf, np.inf)
print(I_1, erreur_1)
print(I_2, erreur_2)


1.7724538509055159 1.4202636780944923e-08
2.9480983632192556e-198 0.0

Avant toute intégration numérique, il convient d'étudier ou/et de représenter la fonction à intégrer de manière à s'assurer que son comportement (présence de singularités, d'importantes variations locales, etc.) ne met pas en défaut la méthode numérique envisagée.