La fonction odeint permet de résoudre numériquement un
système d'équations différentielles ordinaires (EDO) du premier ordre
de la forme :
\[
\left\{
\begin{array}{rcl}
\dot{\vec y} (t) &=& \vec f(\vec y(t), t) \,, \\
\vec y(t_0) &=& \vec y_0 \,,
\end{array}
\right.
\]
et d'obtenir une approximation \(\vec y(t)\) de l'évolution du système
pour des temps \(t\) supérieurs à \(t_0\). Ainsi, il est par exemple
possible de résoudre l'équation (vectorielle) du pendule simple que
nous étudions dans la série 24 en considérant le système:
\[
\left\{
\begin{array}{rcl}
\begin{pmatrix} \dot\theta \\ \dot v \end{pmatrix}
&=&
\begin{pmatrix} v \\ -\omega_{0}^{\,2}\sin\theta \end{pmatrix}
\,, \\ \\
\begin{pmatrix} \theta (0) \\ v(0) \end{pmatrix} &=&
\begin{pmatrix} \theta_0 \\ v_0 \end{pmatrix}\,.
\end{array}
\right.
\]
Les constantes \(\theta_0\) et \(v_0\) correspondent aux deux conditions
initiales et \(\omega_{0}^{\,2} = g/L\) (où \(L\) est la longueur du fil).
La fonction odeint retourne alors un vecteur solution :
\[
\vec y(t) = \begin{pmatrix}
\theta (t) \\ v(t)
\end{pmatrix}\,.
\]
Ainsi, le code permettant de résoudre l'EDO du pendule simple pourrait
débuter de la manière suivante :
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
g = 9.81 ; L = 2 ; omegazerocarre = g/L # constantes
y_0 = np.array([np.pi/6, 0.0]) # vecteur conditions initiales
# ou : y_0 = [np.pi/6, 0.0]
On définit ensuite le membre de droite de l'EDO, f(t,y), sous forme
vectorielle :
def f(t, y):
theta, v = y
return [v, -omegazerocarre*np.sin(theta)]
Cette fonction retourne un tableau de la même forme (shape) que
y.
Il est également nécessaire de construire un vecteur temps dont les éléments correspondent aux instants \(t_n\) pour lesquels nous souhaitons obtenir une valeur approchée de la solution \(y\) (la première entrée de ce tableau devant être la valeur initiale \(t_0\)) :
t_0 = 0 ; T = 10 ; N = 200 # N est le nombre de sous-intervalles
t = np.linspace(t_0, T, N+1) # vecteur contenant N+1 elements t_n
Il convient de noter que la partition choisie au moment de la
construction de t ne sera pas prise en compte par
odeint pour la résolution numérique du problème. En effet,
odeint va adapter le pas \(h\) utilisé en fonction de deux
valeurs (qui correspondent à des tolérances relative et absolue)
fournissant une majoration de l'erreur locale. Ces valeurs
rtol et atol sont des
keyword arguments valant par défaut environ \(1.5\cdot 10^{-8}\).
La solution approchée aux instants donnés par t est
ensuite obtenue par interpolation.
La ligne suivante fournit un tableau solution de dimension \(2\) de forme
(N+1,2) (à savoir ici (201,2)) :
sol = odeint(f, y_0, t, tfirst=True)
Le paramètre optionnel tfirst permet de préciser la
position de la variable t dans la fonction f :
f(y,t) ou f(t,y).
Les solutions peuvent alors être ''décompactées'' :
angle = sol[:,0]
vitesse_angulaire = sol[:,1]
\dots\,et visualisées de manière habituelle :
plt.figure(figsize=(12,8))
plt.plot(t, angle, label=r"angle ${\theta(t)}$")
plt.plot(t, vitesse_angulaire, label=r"vitesse angulaire "\
r"$\dot\theta(t)$")
plt.grid()
plt.title("Solutions pour le pendule simple "\
r"(avec $\theta_0 = {\pi/6}$ et $\dot\theta_0 = {0}$)")
plt.xlabel('t')
plt.legend(loc='best')
plt.show()
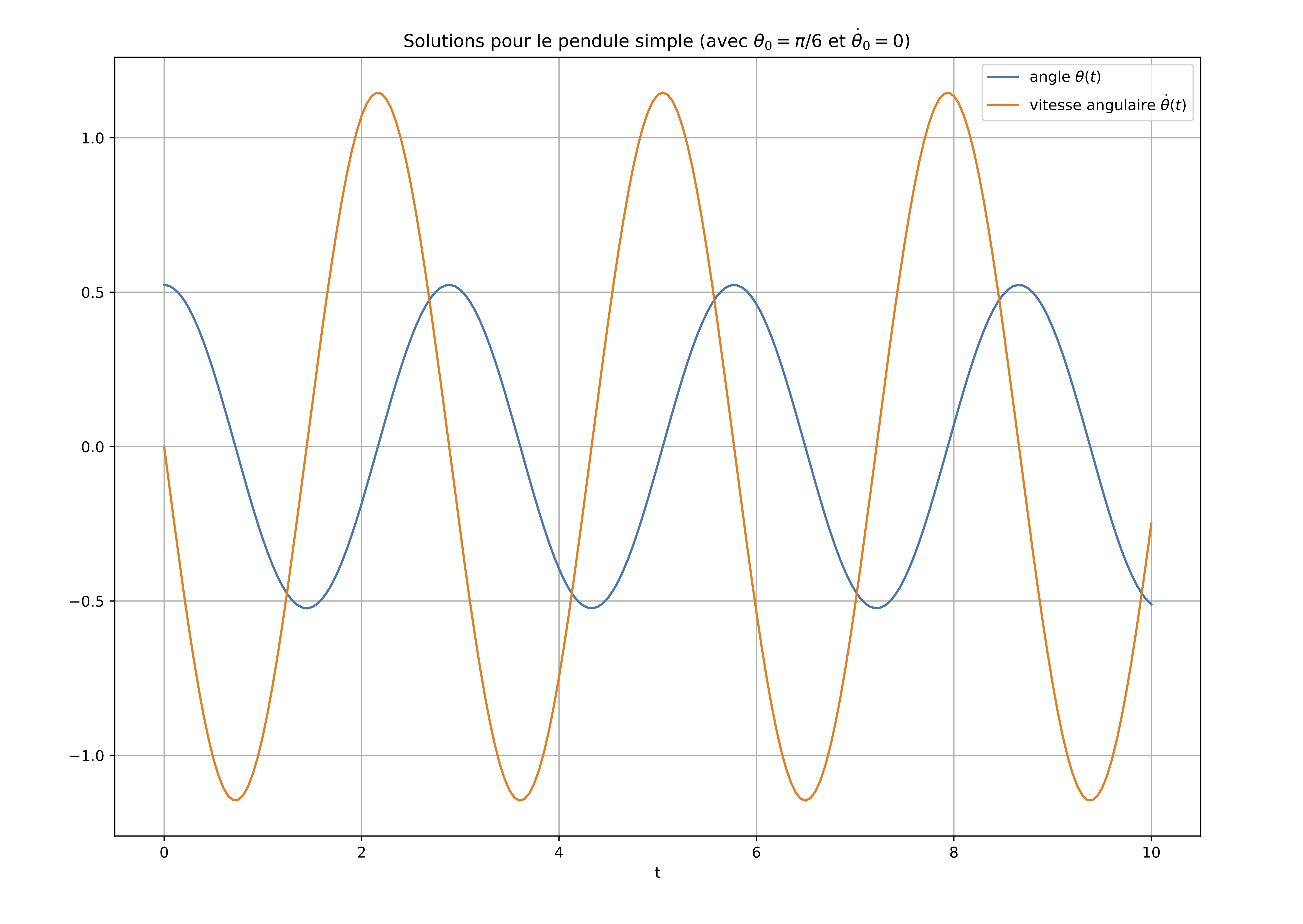
Figure générée :
Le mouvement d'un pendule simple peut également être illustré en représentant la solution dans un espace particulier, appelé espace de phase avec \(\theta\) en abscisse et \(\dot\theta\) en ordonnée :
plt.figure(figsize=(12,8))
plt.plot([min(angle),max(angle)],[0, 0],c='k')
plt.plot([0,0],[min(vitesse_angulaire),max(vitesse_angulaire)],c='k')
plt.plot(angle,vitesse_angulaire)
plt.plot([y_0[0]],[y_0[1]],'or')
plt.grid()
plt.title(r"Représentation dans l'espace de phase "\
rf"($\theta$,$\dot\theta$) de la solution correspondant "\
rf"à $\theta_0 = {y_0[0]:.4f}$ et $\dot\theta_0 = {y_0[1]}$")
plt.xlabel(r'$\theta$')
plt.ylabel(r'$\dot\theta$')
plt.show()
Figure générée :
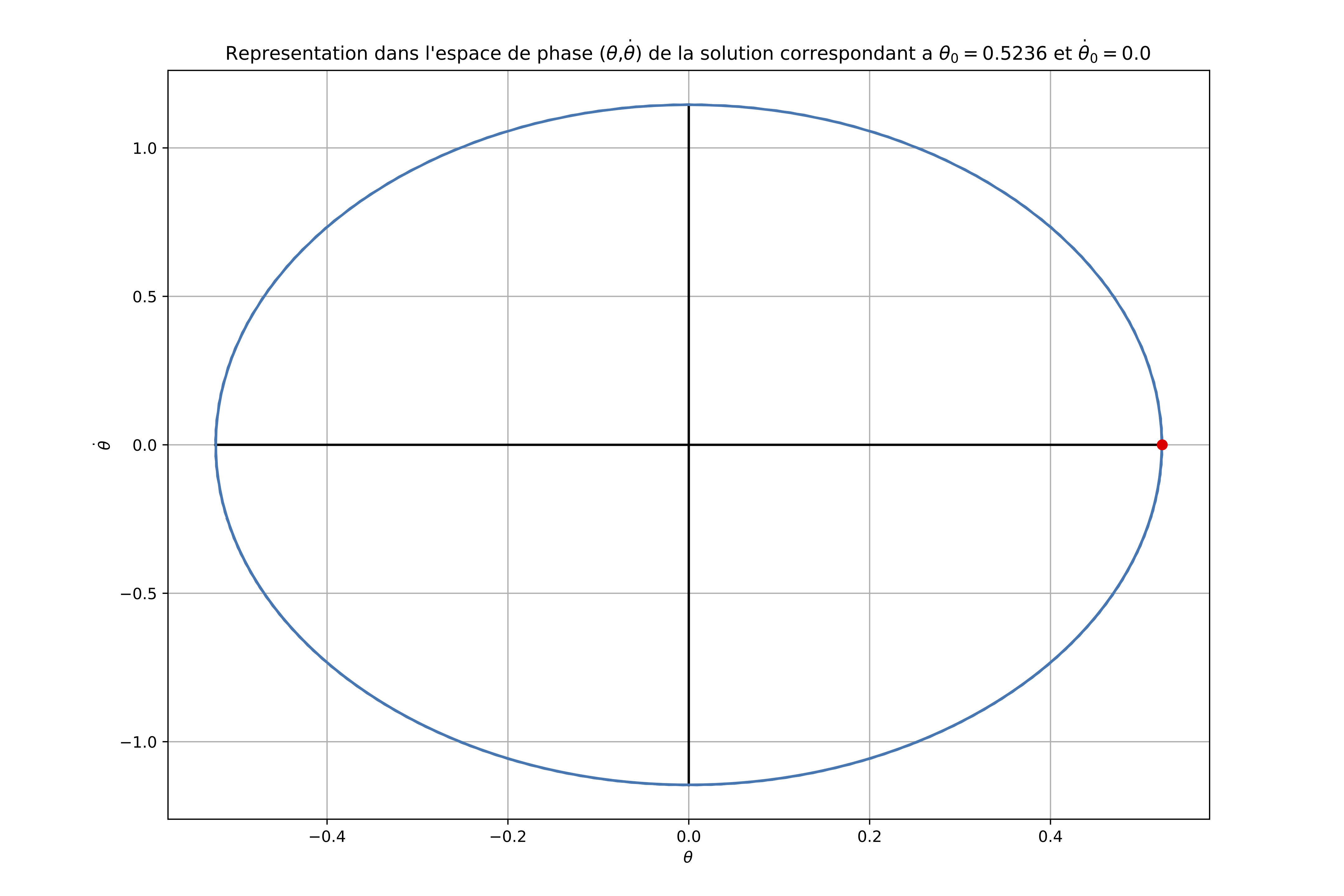
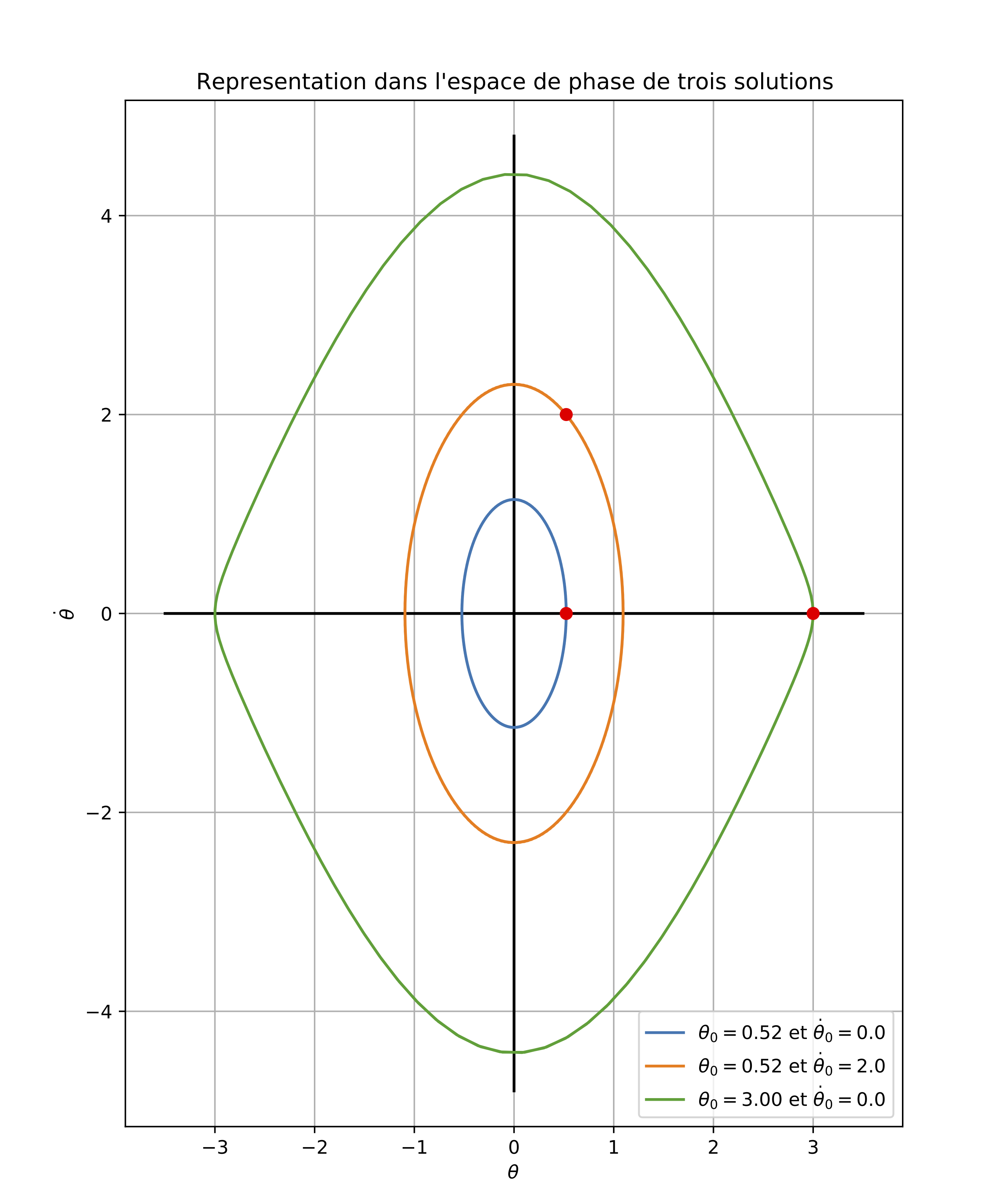
Trois couples différents de conditions initiales (points rouges) fournissent trois courbes différentes :
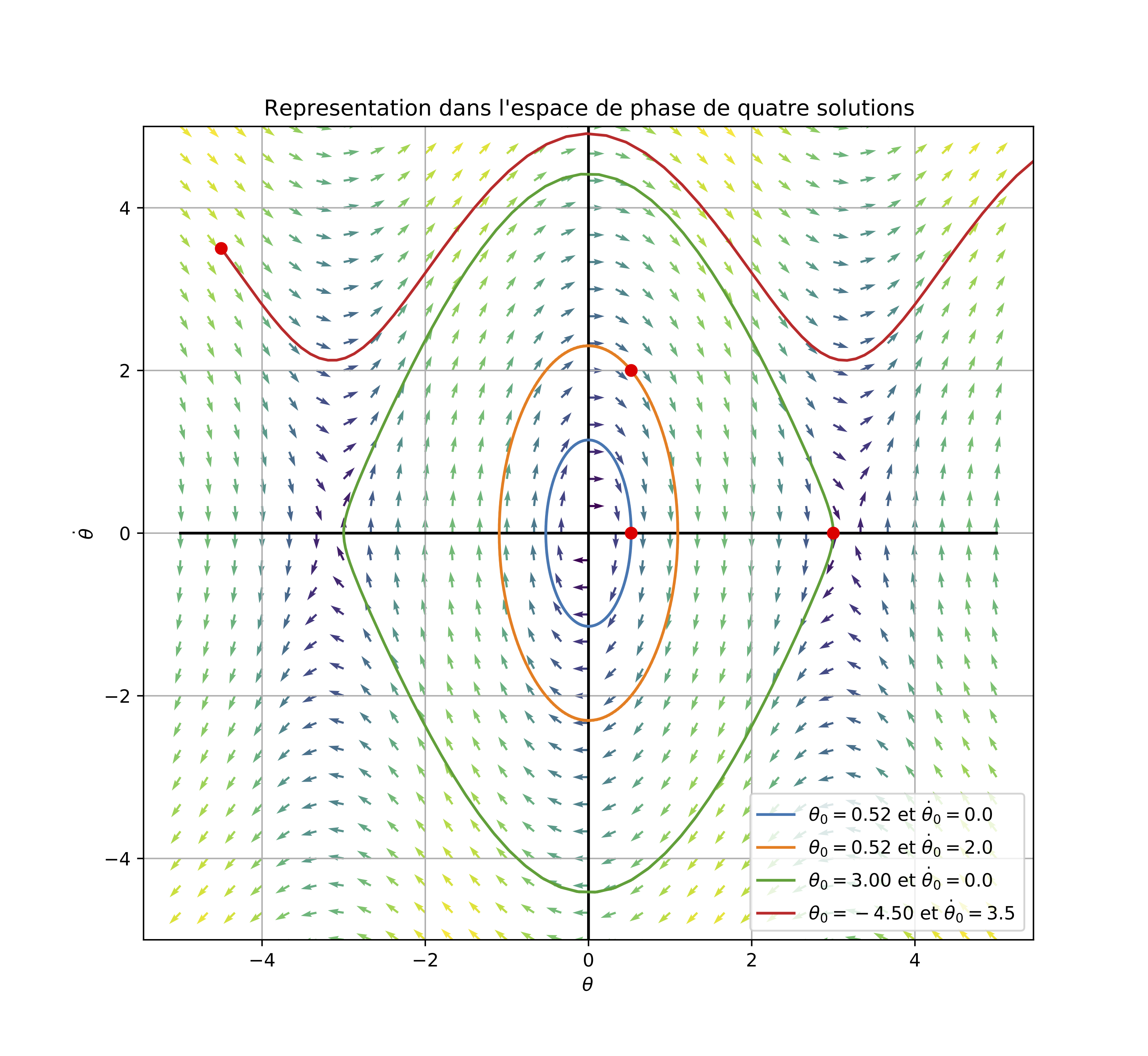
Trajectoires et champ de directions :
Dernière compilation: 2025-05-28 (06:27:05)
Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)
