1.2 Tableaux unidimensionnels

Les tableaux en une dimension, que l'on peut considérer comme étant des ''vecteurs'', c'est-à-dire de simples séquences de nombres, sont des éléments essentiels de tout calcul scientifique.

Construction à partir d'une fonction de NumPy

La bibliothèque Numpy offre plusieurs fonctions permettant de construire de tels tableaux unidimensionnels :

  1. La fonction np.linspace

    Des tableaux de réels (floats) également espacés peuvent être créés à l'aide de la fonction np.linspace(start,stop,num). Ainsi, le code

    import numpy as np x = np.linspace(-2,3,10,endpoint=True,retstep=False) print(x)

    construit un tableau de taille 10 (i.e. un tableau contenant \(10\) éléments (nombres); \(50\) étant la taille par défaut) :

    [-2. -1.44444444 -0.88888889 -0.33333333 0.22222222 0.77777778 1.33333333 1.88888889 2.44444444 3. ]

    \(\rightarrow\) le premier élément est x[0]=-2.

    \(\rightarrow\) le dernier élément est x[-1]=3 (endpoint=True, valeur par défaut)

    \(\rightarrow\) le pas entre chaque valeur est alors donné par \(\dfrac{3-(-2)}{10-1}\).

    Si retstep=True, la fonction retourne un tuple renfermant le tableau et le pas :

    import numpy as np x_vecteur,dx=np.linspace(-2,3,10,endpoint=False,retstep=True) print(x_vecteur,dx) print(type(x_vecteur)) print(type(x_vecteur[1])) print(type(dx)) [-2. -1.5 -1. -0.5 0. 0.5 1. 1.5 2. 2.5] 0.5

    \(\rightarrow\) le pas entre chaque valeur est ici donné par \(\dfrac{3-(-2)}{10}\).

  2. La fonction np.logspace

    La fonction np.logspace(start,stop,num) produit quant à elle un tableau de \(N\) nombres également espacés sur une échelle logarithmique. Les arguments start et stop se refèrent cette fois à une puissance de \(10\) : le tableau commence à \(10^{\text{start}}\) et se termine à \(10^{\text{stop}}\).

  3. La fonction np.arange

    La fonction np.arange(start,stop,step) (''ArrayRANGE'') fournit une troisième manière de créer un tableau de nombres. Cette fonction est similaire à la fonction range (définie au semestre d'automne) permettant de créer des listes. Il est possible d'omettre le premier argument (qui prend alors la valeur \(0\)) et/ou le troisième argument (qui prend alors la valeur \(1\)).

    Cette fonction permet ainsi par exemple de construire un vecteur renfermant les valeurs réelles comprises entre start=-2 et stop=3 (sans cette dernière valeur) séparées de la distance step=0.2 :

    import numpy as np x = np.arange(-2,3,0.2) print(x) [-2.0000000e+00 -1.8000000e+00 -1.6000000e+00 -1.4000000e+00 -1.2000000e+00 -1.0000000e+00 -8.0000000e-01 -6.0000000e-01 -4.0000000e-01 -2.0000000e-01 -4.4408921e-16 2.0000000e-01 4.0000000e-01 6.0000000e-01 8.0000000e-01 1.0000000e+00 1.2000000e+00 1.4000000e+00 1.6000000e+00 1.8000000e+00 2.0000000e+00 2.2000000e+00 2.4000000e+00 2.6000000e+00 2.8000000e+00]
  4. Les fonctions np.zeros, np.ones et np.empty

    Parfois, il peut être utile de construire un vecteur dont toutes les composantes valent \(0\), \(1\) ou ne sont pas initialisées (explicitement) :

    import numpy as np v_zero = np.zeros(3) v_un = np.ones(5, dtype=int) v_vide = np.empty(2) print(v_zero, v_un, v_vide) [0. 0. 0.] [1 1 1 1 1] [-5.73021895e-300 -2.68156159e+154]

    Les fonctions np.zeros(shape), np.ones(shape) et np.empty(shape) ont chacune un argument obligatoire qui représente la forme du tableau (en fait, le plus souvent, il s'agit du nombre d'éléments dans le tableau), et un argument optionnel dtype qui spécifie le type des données du tableau (bool, int, float (défaut) ou complex).

  5. La fonction np.array

    Finalement, un tableau peut être créé à l'aide de la fonction np.array(object) avec pour arguments un container (liste, tuple ou tableau) et éventuellement un paramètre dtype :

    import numpy as np print(np.array([-1,0,2.],dtype=complex)) [-1.+0.j 0.+0.j 2.+0.j]

    Si l'argument dtype est omis, la fonction np.array promeut automatiquement tous les éléments du tableau au type de l'entrée la plus générale du tableau (qui serait dans l'exemple ci-dessus le type float).

    Comme le montrent les quelques lignes de code suivantes, Numpy apporte à Python une grande diversité de types numériques :

    import numpy as np x=0.123456789123456789123456789 # print('x =',x) print('Python (default) type :',type(x)) print('\n') # y=np.array([0.123456789123456789123456789]) print('y =',y) print('y[0] =',y[0]) print('y (Numpy default) type :',type(y)) print('y (Numpy default) data type :',y.dtype) print('y[0] (Numpy default) type :',type(y[0])) print('\n') # z16=np.array([0.123456789123456789123456789],dtype=np.float16) print('NumPy, 16bits type :',z16.dtype) print('z[0] =',z16[0]) print('\n') # z32=np.array([0.123456789123456789123456789],dtype=np.float32) print('NumPy, 32bits type :',z32.dtype) print('z[0] =',z32[0]) print('\n') # z64=np.array([0.123456789123456789123456789],dtype=np.float64) print('NumPy, 64bits type :',z64.dtype) print('z[0] =',z64[0])

    Dans la sortie produite, on note que le type numpy.float64 (ou numpy.double) fournit la même précision que le type float natif :

    x = 0.12345678912345678 Python (default) type : y = [0.12345679] y[0] = 0.12345678912345678 y (Numpy default) type : y (Numpy default) data type : float64 y[0] (Numpy default) type : NumPy, 16bits type : float16 z[0] = 0.1235 NumPy, 32bits type : float32 z[0] = 0.12345679 NumPy, 64bits type : float64 z[0] = 0.12345678912345678
Construction à partir d'un objet préexistant

Supposons que l'on définisse un vecteur x dont les composantes sont, par exemple, régulièrement espacées. Il peut être utile de définir un vecteur de la même taille et du même type que x. Trois constructeurs différents permettent d'obtenir un vecteur non initialisé (''vide''), un vecteur rempli de \(0\) et un vecteur ne contenant que des \(1\) : np.empty_like(), np.zeros_like() et np.ones_like().

Ainsi, le code

import numpy as np x = np.linspace(0,9,10, dtype=int) y_vide = np.empty_like(x) y_zero = np.zeros_like(x) y_un = np.ones_like(x) print(y_vide, y_zero, y_un)

produit la sortie suivante :

[ 0 4607182418800017408 4611686018427387904 4613937818241073152 4616189618054758400 4617315517961601024 4618441417868443648 4619567317775286272 4620693217682128896 4621256167635550208] [0 0 0 0 0 0 0 0 0 0] [1 1 1 1 1 1 1 1 1 1]
Opérations arithmétiques sur les tableaux

En Python, il est possible d'additionner, de soustraire, de multiplier ou de diviser deux vecteurs de même taille. Durant ces opérations, la \(i\)ème composante du vecteur résultant est obtenue par l'addition, la soustraction, la multiplication ou la division des \(i\)ème composantes des deux vecteurs :

import numpy as np v_1 = np.array([-1,2,4]) v_2 = np.linspace(1,2,3) print(v_1, v_2) print(v_1+v_2, v_1-v_2) print(v_1*v_2, v_1/v_2) [-1 2 4] [1. 1.5 2. ] [0. 3.5 6. ] [-2. 0.5 2. ] [-1. 3. 8.] [-1. 1.33333333 2. ]

Les opérations d'addition et de soustraction de deux vecteurs sont identiques à celles définies en géométrie euclidienne. En revanche, avec des vecteurs habituels, le produit (scalaire) entre deux vecteurs, par exemple \(\vec v_1=(a,b)\) et \(\vec v_2=(c,d)\), fournit un scalaire : \[ \vec v_1 \cdot \vec v_2 = ac+bd\,, \] alors que dans NumPy le produit de deux ndarray est un tableau de même taille. ''Vectoriellement'', cela aurait la signification suivante : \[ v\_1 * v\_2 = [ac,bd]\,. \] Remarquons également qu'en géométrie, la division d'un vecteur par un autre n'a pas de sens, alors que c'est une opération bien définie en Python : \[ v\_1 / v\_2 = [a/c,b/d]\,. \]

En géométrie, on est fréquemment amené à multiplier un vecteur par un scalaire. Comme le montre le code suivant, NumPy autorise le même type de manipulations :

import numpy as np v = np.array([-1,2,4]) print(5*v, v*5) print(v/5, 5/v) print(v**4) print(v+5) [-5 10 20] [-5 10 20] [-0.2 0.4 0.8] [-5. 2.5 1.25] [ 1 16 256] [4 7 9]

De plus, NumPy fournit des fonctions appelées universal functions (ou simplement ufuncs) qui peuvent être appliquées à un scalaire, de manière à produire un scalaire, ou à un tableau de façon à générer un tableau de même taille (en s'appliquant alors à chaque composante).

Parmi ces ufuncs, on trouve notamment les fonctions\(\ldots\)

Ainsi, il est par exemple possible de construire très facilement un vecteur y dont les composantes sont les racines carrées des composantes correspondantes d'un vecteur x :

import numpy as np x = np.linspace(0,9,10) y = np.sqrt(x) print(x) print(y) [0. 1. 2. 3. 4. 5. 6. 7. 8. 9.] [0. 1. 1.41421356 1.73205081 2. 2.23606798 2.44948974 2.64575131 2.82842712 3. ]

Notons que Python permet le calcul de la racine carrée d'un nombre négatif pour autant que l'on manipule des nombres complexes.

Rappel: La racine carrée de \(-1\) est le nombre complexe \( i\) : \( i=\sqrt{-1}\). En Python, ce nombre se note j.

Dans le code suivant, la troisième ligne produit un ''warning'' (et retourne une composante nan (not a number)) parce que les éléments de v sont des nombres réels. La cinquième ligne en revanche s'exécute sans problème, les éléments de a*v étant complexes. import numpy as np v = np.array([-1,2,4]) print(np.sqrt(v)) a = complex(1,0) print(np.sqrt(a*v)) [ nan 1.41421356 2. ] [0. +1.j 1.41421356+0.j 2. +0.j]

Dans l'exemple suivant, NumPy calcule le logarithme où il le peut, et retourne nan si l'opération est illégale (calcul du logarithme d'un nombre négatif) et -inf pour le logarithme de zéro. Les autres valeurs dans le tableau sont retournées correctement :

import numpy as np b = np.arange(-2.,4,1) print(np.log(b)) [ nan nan -inf 0. 0.69314718 1.09861229]

Nous savons qu'une expression telle que \(\vec v\gt 0\), où \(\vec v\) est un vecteur n'a pas de sens. Dans le cas d'un tableau unidimensionnel de NumPy, une telle opération de comparaison est autorisée, élément par élément. On obtient un vecteur contenant les valeurs booléennes (valeurs ''de vérité'') True ou False :

import numpy as np v = np.linspace(-2,2,9) y = v > 0 print(v) print(y) [-2. -1.5 -1. -0.5 0. 0.5 1. 1.5 2. ] [False False False False False True True True True]

Un vecteur ''logique'' tel que le vecteur y ci-dessus permet par exemple de calculer facilement la valeur absolue de x :

import numpy as np v = np.linspace(-2,2,9) w = v w[w<0]=-w[w<0] print(w) print(v) [2. 1.5 1. 0.5 0. 0.5 1. 1.5 2. ] [2. 1.5 1. 0.5 0. 0.5 1. 1.5 2. ]

Remarquons que pour conserver le vecteur v original, il faudrait remplacer la troisième ligne par w = v.copy().

Indexation et découpage (slicing) des tableaux

Les tableaux peuvent être découpés de la même manière que les listes et on accède à un élément d'un tableau unidimensionnel grâce à l'indice de l'élément placé entre des crochets qui suivent l'identificateur du tableau.

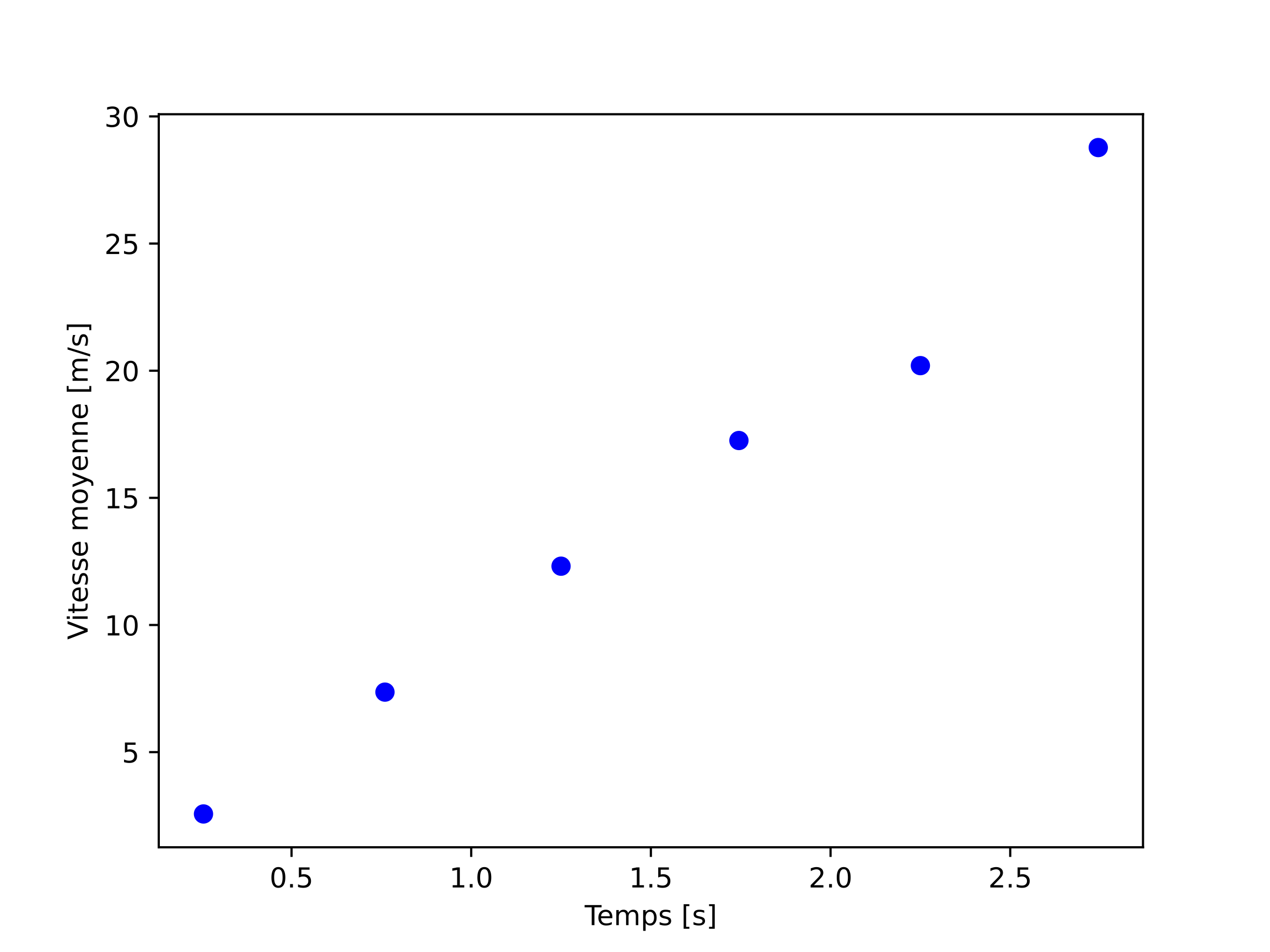
Pour comprendre comment fonctionne ce découpage, nous allons imaginer une expérience de chute libre, durant laquelle la distance verticale y (en mètres) parcourue par un objet est mesurée en fonction du temps t (en secondes). Les mesures permettent alors de remplir les deux tableaux suivants :

import numpy as np y = np.array([0,1.31,4.99,10.9,19.7,29.8,43.9]) t = np.array([0,0.51,1.01,1.49,2.,2.5,2.99])

Il est possible de calculer la vitesse moyenne de l'objet en s'intéressant au taux de variation de la position par rapport au temps : \[ v_{\text{moy},i} = \frac{y_i-y_{i-1}}{t_i-t_{i-1}}\,,~~i\ge 1\,, \] où les \(y_i\) et les \(t_i\) sont les éléments des tableaux y et t.

Pour ce faire, nous envisageons le découpage des tableaux y et t. Par exemple, pour y, nous allons considérer

print(y) # tableau complet des mesures de distance print(y[1:]) # tableau amputé de la première mesure de distance print(y[:-1]) # tableau amputé de la dernière mesure de distance [ 0. 1.31 4.99 10.9 19.7 29.8 43.9 ] [ 1.31 4.99 10.9 19.7 29.8 43.9 ] [ 0. 1.31 4.99 10.9 19.7 29.8 ]

et faire la différence élément par élément (idem pour le tableau t) :

v_moyenne = (y[1:]-y[:-1])/(t[1:]-t[:-1]) print(v_moyenne) [ 2.56862745 7.36 12.3125 17.25490196 20.2 28.7755102 ]

La division se fait également élément par élément et le tableau v_moyenne obtenu contient un élément de moins que les tableaux y et t de départ. Il est alors naturel d'associer les vitesses obtenues à un nouveau tableau temporel dont les entrées correspondent à une moyenne entre deux mesures de temps successives:

t_moyenne = (t[1:]+t[:-1])/2 print(t_moyenne) [0.255 0.76 1.25 1.745 2.25 2.745]

Les tableaux v_moyenne et t_moyenne renferment ainsi le même nombre d'éléments.

Nous verrons au chapitre suivant comment représenter de telles données expérimentales :

Une telle représentation permet d'avoir rapidement une ''vérification'' visuelle du comportement (linéaire) de la vitesse en fonction du temps dans le cas de la chute libre : \[ v(t) = A\, t\,, \hbox{où }A \hbox{ est une constante}\,. \]

Dernière compilation: 2025-05-28 (06:27:04)

Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)