Dans une méthode d'intégration composite, on applique une formule de quadrature à un sous-intervalle \([x_i,x_{i+1}]\) a priori quelconque. Pour pouvoir étudier et comparer les différentes formules de quadrature dans le cadre d'un formalisme général, nous allons remplacer \([x_i,x_{i+1}]\) par l'intervalle ''standard'' (''canonique'') \([-1,+1]\).
Pour ce faire, nous allons effectuer le changement de variable \(x\in [x_i,x_{i+1}]\rightarrow t\in [-1,+1]\) :
\[ t = 2\frac{x-x_i}{x_{i+1}-x_i}-1 \leftrightarrow x = \frac{x_i+x_{i+1}}{2} + \frac{x_{i+1}-x_i}{2}t\,. \]On note ainsi en particulier que \(x=x_i ~\leftrightarrow~ t=-1\) et \(x=x_{i+1} ~\leftrightarrow~ t=+1\).
Ainsi, l'intégrale définie de \(f(x)\) sur \([x_{i},x_{i+1}]\) peut alors s'écrire
\[\begin{aligned} \int_{x_i}^{x_{i+1}}{f(x)dx} = & \int_{-1}^{+1}{f\left(\frac{x_i+x_{i+1}}{2} + \frac{x_{i+1}-x_i}{2}t\right)\dfrac{x_{i+1}-x_i}{2}dt} \\ \equiv & \,\frac{x_{i+1}-x_i}{2}\int_{-1}^{+1}{g_i(t)dt}\,, \end{aligned}\]où l'on a utilisé le lien entre \(dx\) et \(dt\) donné par le changement de variable,
\[ dx = \dfrac{x_{i+1}-x_i}{2}dt\,, \]et introduit la fonction \[g_i(t) = f\left(\frac{x_i+x_{i+1}}{2} + \frac{x_{i+1}-x_i}{2}t\right)\] qui est une fonction continue définie sur l'intervalle \([-1,+1]\).
Soit \(g\) une fonction continue sur l'intervalle \([-1,+1]\), la formule de quadrature
\[ J(g) = \sum_{j=1}^{M}{w_j\,g(t_j)}\,, \]est une approximation de \(\int_{-1}^{+1}{g(t)dt}\) dans laquelle interviennent
Une formule de quadrature \(J\) telle que celle définie ci-dessus est dite exacte pour les polynômes de degré \(r\ge 0\) si
\[ J(p) = \int_{-1}^{+1}{p(t)dt} \]pour tout polynôme \(p\) de degré inférieur ou égal à \(r\).
Nous allons commencer par indiquer trois exemples de formules de quadrature de la forme
\[ J(g) = \sum_{j=1}^{M}{w_j\,g(t_j)} \]avant de chercher à déterminer au mieux les \(M\) noeuds \(t_j\) et les \(M\) poids \(w_j\) associés.
Exemple:[1 noeud]
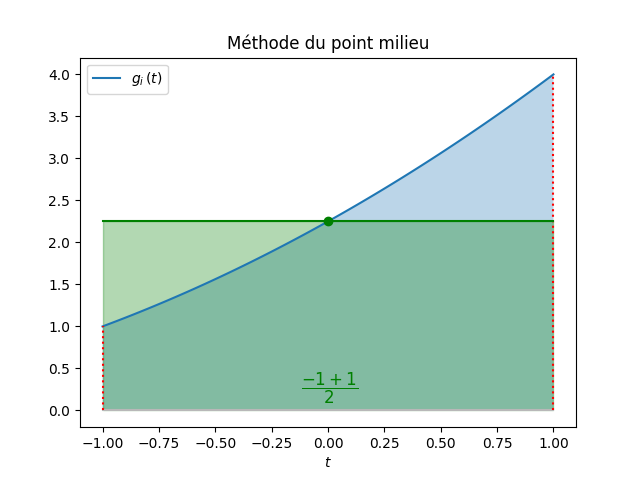
La formule du point milieu (PM) correspond à une méthode à 1 point (\(M=1\)), le point (noeud) étant choisi au milieu de \([-1,+1]\) : \(t_1=0\). En reprenant les notations ci-dessus, il vient
\[ J^{\text{PM}}(g) = \sum_{j=1}^{M=1}{w_j\,g(t_j)} = w_1\,g(t_1) =w_1\,g(0) = \underbrace{2}_{\text{''base"}}\cdot \underbrace{g(0)}_{\text{''hauteur"}}\!\!\!. \]On constate que \(w_1=2\). En revenant à la fonction \(f\) et à l'intervalle de départ \([x_i,x_{i+1}]\), l'approximation cherchée de \(\int_{x_i}^{x_{i+1}}{f(x)dx}\) est
\[ J_i^{\text{PM}}(f) = \frac{x_{i+1}-x_i}{2}\cdot 2\cdot f\left(\frac{x_i+x_{i+1}}{2}\right) = (x_{i+1}-x_i)\cdot f\left(\frac{x_i+x_{i+1}}{2}\right)\,. \]En guise d'exemple concret, prenons \(f(x)= x^2\) que l'on cherche à intégrer sur \([x_{i+1},x_i] = [1,2]\). On a alors \(g_i(t)=\left(\frac{3}{2}+\frac{1}{2}t\right)^2\) et
\[ \int_{x_i}^{x_{i+1}}{\!\!\!\!\!\!f(x)dx} = \int_{1}^{2}{\!\!\!x^2 dx} = \frac{x_{i+1}-x_i}{2}\int_{-1}^{+1}{\!\!\!\!\!\!g_i(t)dt} = \frac{1}{2}\underbrace{\int_{-1}^{+1}{\left(\frac{3}{2}+\frac{1}{2}t\right)^2dt}}_{\text{approximé par }J^{\text{PM}}(g_i)}.\]Comme \(J^{\text{PM}}(g_i) =2\cdot g_i(0)\), l'approximation cherchée est donnée par \(J_i^{\text{PM}}(f) = \dfrac{1}{2}2g_i(0) = g_i(0) = \dfrac{9}{4}\).
Exemple:[2 noeuds]
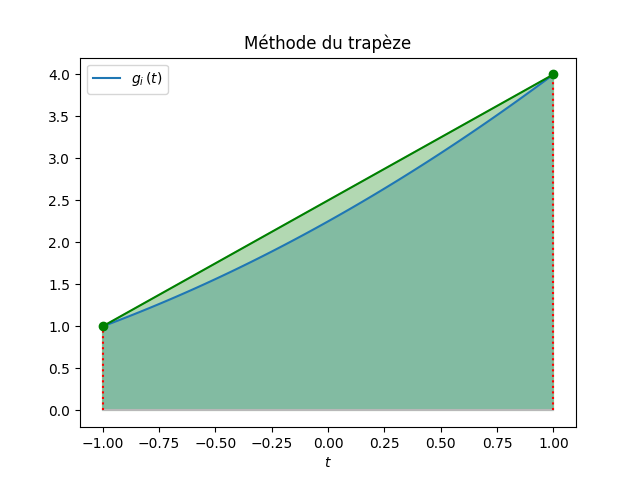
La formule du trapèze (TR) correspond à une méthode à 2 points (\(M=2\)), les deux points (noeuds) étant choisis au début et à la fin de \([-1,+1]\) : \(t_1=-1\) et \(t_2=+1\). Ainsi,
\[\begin{aligned} J^{\text{TR}}(g) =& \sum_{j=1}^{M=2}{w_j\,g(t_j)} = w_1\,g(-1) + w_2\,g(+1) \\ =& \underbrace{2}_{\text{''base"}}\cdot \underbrace{\frac{g(-1)+g(+1)}{2}}_{\text{''hauteur moyenne"}} = g(-1)+g(+1)\,. \end{aligned}\]On constate que \(w_1=1=w_2\). En revenant à la fonction \(f\) et à l'intervalle de départ \([x_i,x_{i+1}]\), l'approximation cherchée de \(\int_{x_i}^{x_{i+1}}{f(x)dx}\) est
\[ J_i^{\text{TR}}(f) = (x_{i+1}-x_i) \frac{f(x_i)+f(x_{i+1})}{2}\,. \]Cas concret discuté plus haut :
Exemple:[3 noeuds]
La formule dite de Simpson (S) correspond à une méthode à 3 points (\(M=3\)), les trois points (noeuds) étant choisis au début, au milieu et à la fin de \([-1,+1]\) : \(t_1=-1\), \(t_2=0\) et \(t_3=+1\). Ainsi,
\[ J^{\text{S}}(g) = \sum_{j=1}^{M=3}{w_j\,g(t_j)} = w_1\,g(-1) + w_2\,g(0) + w_3\,g(+1)\,. \]En exercices et plus loin, nous verrons que l'approximation numérique peut être optimisée en choisissant les poids suivants :
\[ w_1=\frac{1}{3}\,, w_2=\frac{4}{3} \text{ et } w_3=\frac{1}{3}\,. \]En revenant à la fonction \(f\) et à l'intervalle de départ \([x_i,x_{i+1}]\), l'approximation cherchée de \(\int_{x_i}^{x_{i+1}}{f(x)dx}\) est
\[ J_i^{\text{S}}(f) = (x_{i+1}-x_i) \left(\frac{1}{6} f(x_i) + \frac{4}{6}f\left(\frac{x_{i+1}+x_i}{2}\right) + \frac{1}{6}f(x_{i+1})\right)\,. \]Cas concret discuté plus haut :
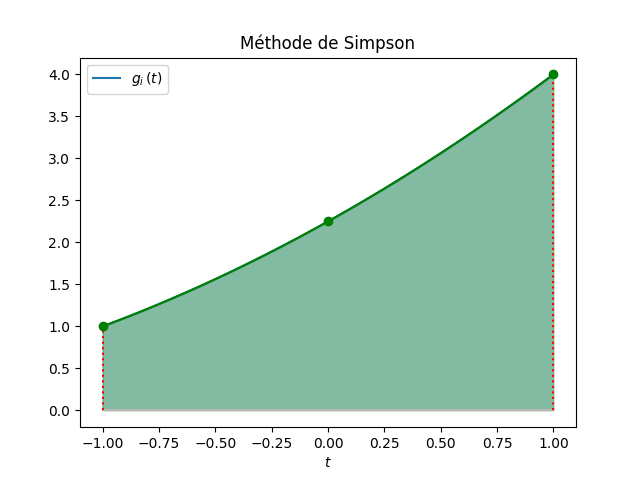
L'intégration numérique par la méthode de Simpson est, pour ce cas concret, exacte.
En supposant avoir choisi les \(M\) noeuds (points) \(t_j\), on peut se demander comment déterminer les \(M\) poids \(w_j\) associés pour approximer au mieux \(\int_{-1}^{+1}{g(t)dt}\).
Théorème:
Soient \(t_1\lt t_2\lt \ldots\lt t_M\), \(M\) points distincts de l'intervalle canonique \([-1,1]\), et soit \(\varphi_1\), \(\varphi_2\), \(\ldots\), \(\varphi_M\) la base de Lagrange de \(\mathbb{P}_{M-1}\) associée à ces \(M\) points.
Alors, la formule de quadrature
\[ J(g) = \sum_{j=1}^{M}{w_jg(t_j)} \]est exacte pour les polynômes de degré \(M-1\) au moins si et seulement si
\[ w_j = \int_{-1}^{+1}{\varphi_j(t)dt}\,,\text{ où } j=1,2,\dots,M\,. \]Sens \(\Rightarrow\)
En supposant la formule exacte, il vient :
\[ J(p) = \sum_{j=1}^{M}{w_jp(t_j)} = \int_{-1}^{+1}{p(t)dt}\,,\forall p\in\mathbb{P}_{M-1}\,. \]Ainsi, cette relation doit être en particulier vraie pour \(p=\varphi_k\), avec \(k=1,2,\dots,M\). Par conséquent,
\[ J(\varphi_k) = \underbrace{\sum_{j=1}^{M}{w_j\varphi_k(t_j)}}_{=w_k\cdot 1=w_k}=\int_{-1}^{+1}{\varphi_k(t)dt}\,. \]Sens \(\Leftarrow\)
Soit \(p\in \mathbb{P}_{M-1}\), \(p\) quelconque. On peut écrire le développement de \(p\) dans la base de Lagrange associée aux points \(t_1, t_2, \ldots, t_M\) :
\[ p(t) = \sum_{j=1}^{M}{p(t_j)\varphi_j(t)}\,. \]Il vient alors
\[ \int_{-1}^{+1}{p(t)dt} = \sum_{j=1}^{M}{p(t_j)\underbrace{\int_{-1}^{+1}{\varphi_j(t)dt}}_{=w_j\text{ (par hyp.)}}} = \sum_{j=1}^{M}{p(t_j)w_j}=J(p)\,. \]Remarque:
Notons tout d'abord que \(\sum_{j=1}^{M}{1\cdot \varphi_j(t)}\) est le polynôme \(p\in \mathbb{P}_{M-1}\) qui vaut \(1\) aux points \(t_1, t_2, \ldots, t_M\). Il s'agit de la fonction constante égale à \(1\).
On peut alors faire une observation intéressante :
\[ \sum_{j=1}^{M}{w_j} = \sum_{j=1}^{M}{\int_{-1}^{+1}{\varphi_j(t)dt}} = \int_{-1}^{+1}{\Big(\underbrace{\sum_{j=1}^{M}{\varphi_j(t)}}_{=1}\Big)dt} = \int_{-1}^{+1}{1\cdot dt} = 2\,. \]On constate que la somme des poids est toujours égale à \(2\). C'est ce que l'on peut vérifier dans le cas des trois exemples donnés plus haut dans cette section.
Dernière compilation: 2025-05-28 (06:27:05)
Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)
