ICS CMS | R. Sauser (EPFL)

6.1 Introduction

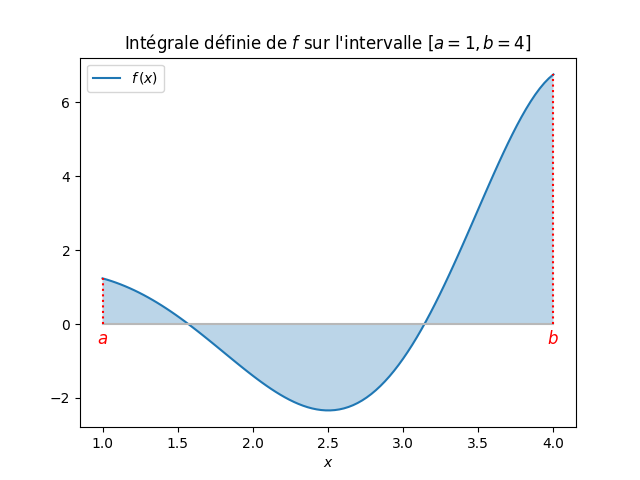
Soit \(f: x\in [a,b]\rightarrow f(x)\in\R\) une fonction continue donnée sur l'intervalle \([a,b]\), on cherche à calculer numériquement l'intégrale définie

\[ I = \int_{a}^{b}{f(x)dx}\,. \]

On peut imaginer approcher numériquement \(I\) grâce à une méthode (on parle parfois de formule) d'intégration (ou de quadrature) directement sur l'intervalle \([a,b]\) de départ.

Souvent, on préfère créer une partition de \([a,b]\) et intégrer dans les sous-intervalles de \([a,b]\) définis par la partition. On parle alors de méthode de quadrature composite.

Une partition de \([a,b]\) est un ensemble de \((N+1)\) points \(x_0, x_1, x_2,\dots, x_N\) tels que

\[ a=x_0< x_1< x_2<\dots< x_N=b\,. \]

Ces points partionnent l'intervalle \([a,b]\) en \(N\) sous-intervalles \([x_i,x_{i+1}]\), \(i=0,1,2,\dots,N-1\).

Une partition se caractérise par sa finesse qui est le nombre réel \[ h = \max_{0\le i \le N-1}{|x_{i+1}-x_i|}\,. \]

En général, on pose

\[ h=\frac{b-a}{N} \]

\[ x_i = a + ih\,,\text{ avec } i=0,1,\dots,N\,. \]

On parle alors de partition régulière de \([a,b]\) et le nombre \(h\) est le pas de la partition.

Après avoir partitionné l'intervalle \([a,b]\), l'intégrale définie s'écrit

\[ I = \int_{a}^{b}{f(x)dx} = \sum_{i=0}^{N-1}{\int_{x_i}^{x_{i+1}}{f(x)dx}} \]

et on cherche donc alors à approcher numériquement les intégrales \(\int_{x_i}^{x_{i+1}}{f(x)dx}\) par des formules (méthodes) de quadrature (d'intégration). Parmi les méthodes d'intégration simples, on peut citer :

les méthodes à un point qui s'inspirent du théorème de la moyenne du calcul intégral selon lequel il existe \(\bar x\in [x_i,x_{i+1}]\) tel que \[ I = \int_{x_i}^{x_{i+1}}{f(x)dx} = (x_{i+1}-x_i)\cdot f(\bar x)\,. \] Le point \(\bar x\) n'est pas connu et on peut envisager de se contenter de choisir au mieux un point entre \(x_i\) et \(x_{i+1}\). C'est ce que fait
- la méthode du point de gauche où on utilise \(x_i\) ,
- la méthode du point de droite où on utilise \(x_{i+1}\) ,
- la méthode de Riemann où on utilise un point au hasard dans \([x_i,x_{i+1}]\) ,
- la méthode du point milieu où on utilise le point milieu \((x_i+x_{i+1})/2\) :
  L'aire de chacun des rectangles verts est donnée par \[ \underbrace{(x_{i+1}-x_i)}_{''\text{base}''}\cdot \underbrace{f\left(\dfrac{x_i+x_{i+1}}{2}\right)}_{''\text{hauteur}''}\,. \]
les méthodes à deux points telles que la méthode du trapèze :
L'aire de chacun des trapèzes verts est donnée par \[ (x_{i+1}-x_i) \cdot \dfrac{f(x_i)+f(x_{i+1})}{2}\,. \]

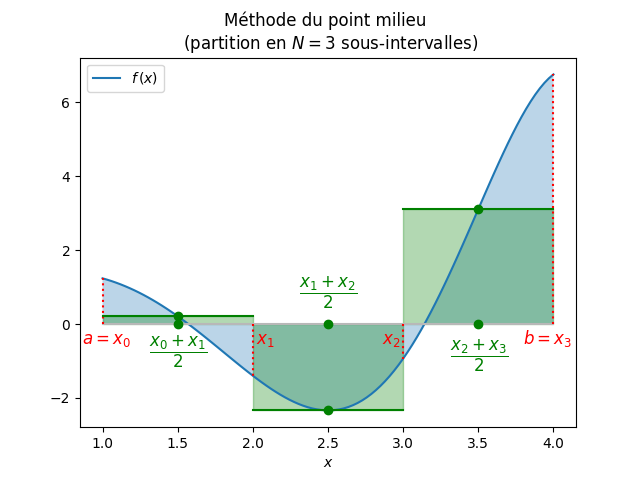
Les méthodes à un point reviennent à approximer la fonction \(f\) par un polynôme de degré zéro passant par le point, i.e. à approximer \(f\) par une fonction constante.

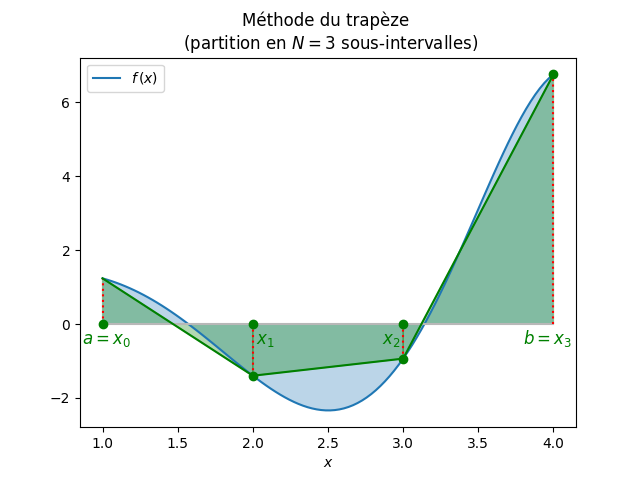
Les méthodes à deux points consistent à approximer la fonction \(f\) par un polynôme de degré un passant par les deux points, i.e. à approximer \(f\) par une fonction affine.

En ayant déterminé la fonction polynomiale passant par un certain nombre de points de la fonction \(f\), on peut alors aisément déterminer une approximation de l'intégrale définie en déterminant l'aire sous la fonction polynomiale. Dans la section suivante, nous allons nous intéresser à ce polynôme d'interpolation (on parle parfois ''d'interpolant'').