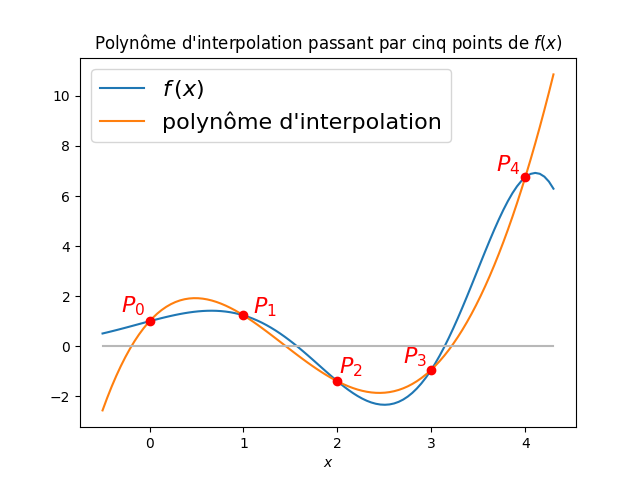
Dans cette section, nous allons chercher à interpoler une fonction \(f\) à l'aide d'un polynôme \(p\) de degré \(n\). Plus précisément, nous allons déterminer un polynôme d'interpolation \(p\in \mathbb{P}_n\) (\(\mathbb{P}_n\) étant l'espace vectoriel des polynômes de degré inférieur ou égal à \(n\)) passant par \((n+1)\) points \(P_i=(x_i, p_i)\), \(i=0,1,2, \dots, n\), avec \(p_i = p(x_i)\equiv f(x_i)\).
Dans le cas de deux points, le polynôme d'interpolation correspond à l'unique droite passant par les deux points. Dans le cas de trois points, le polynôme d'interpolation correspond à l'unique parabole passant par les trois points.
Ces deux résultats peuvent être généralisés : il existe un seul polynôme de degré inférieur ou égal à \(n\) passant par \((n+1)\) points donnés.
Supposons qu'il y ait deux polynômes \(p_1\) et \(p_2\) (de degré inférieur ou égal à \(n\)) passant par les \((n+1)\) points donnés. On remarque que le polynôme \(p_3 = p_2 - p_1\) est donc de degré inférieur ou égal à \(n\) et possède \((n+1)\) zéros distincts \(x_0,x_1,\dots,x_n\). Or, un polynôme (non nul) de degré inférieur ou égal à \(n\) possède au plus \(n\) racines distinctes. On conclut que \(p_3\) est le polynôme constant nul et par suite que \(p_1=p_2\).
Nous allons essayer de trouver ce polynôme d'interpolation en le construisant à partir d'une base de fonctions polynomiales.
Commençons par chercher le polynôme passant par \(n\) points d'ordonnées \(p_j\) égales à zéro, et un point d'ordonnée \(p_k\) non nulle. En posant la valeur de \(p_k\) égale à \(1\), il est facile de se convaincre que le polynôme de degré \(n\) \(\varphi_k(x)\) suivant vérifie \(p_i = \varphi_k(x_i)\) dans le cas de ces \((n+1)\) points particuliers :
\[\begin{aligned} \varphi_k(x) =& \frac{(x-x_0)(x-x_1)\dots (x-x_{k-1})(x-x_{k+1})\dots(x-x_n)} {(x_k-x_0)(x_k-x_1)\dots (x_k-x_{k-1})(x_k-x_{k+1})\dots(x_k-x_n)} \\ =& \Pi_{j=0, j\ne k}^{n}{\frac{x-x_j}{x_k-x_j}}\,. \end{aligned}\]On note que le numérateur de chacun des polynômes \(\varphi_k(x)\) est un produit de \(n\) termes \((x-x_j)\). Il s'agit donc d'un polynôme de degré \(n\). Le dénominateur est quant à lui une constante. Ainsi, on a bien que
On montre ci-dessous que les polynômes \(\varphi_0\), \(\varphi_1\), \(\dots\), \(\varphi_n\) ainsi définis sont linéairement indépendants et forment une base de \(\mathbb{P}_n\) appelée base de Lagrange associée aux abscisses (noeuds) \(x_0\), \(x_1\), \(\dots\), \(x_n\). Ainsi, l'unique polynôme \(p\) cherché vérifiant \(p_i = p(x_i)\), \(\forall i\), \(i=0,1,\dots,n\), est donné, dans la forme de Lagrange, par
\[ p(x) = p_0\varphi_0(x) + p_1\varphi_1(x) + \dots + p_n\varphi_n(x) = \sum_{i=0}^{n}{p_i\varphi_i(x)}\,. \]Ce polynôme est le polynôme d'interpolation associé aux points \(P_i=(x_i,p_i)\), \(0\le i\le n\).
Théorème: Les polynômes \(\varphi_0\), \(\varphi_1\), \(\dots\), \(\varphi_n\) sont a) linéairement indépendants et b) forment une base de \(\mathbb{P}_n\).
a)
Commençons par montrer que les polynômes \(\varphi_i\) sont linéairement indépendants. Imaginons que \(\alpha_0\), \(\alpha_1\), \(\dots\), \(\alpha_n\) sont \((n+1)\) nombres réels tels que \(\sum_{i=0}^{n}{\alpha_i\varphi_i(x)}=0\), \(\forall x\in\R\).
Alors, pour \(x=x_k\), on obtient
\[ 0=\sum_{i=0}^{n}{\alpha_i\varphi_i(x_k)} = \alpha_k\cdot 1 = \alpha_k\,. \]Par conséquent, tous les \(\alpha_k\), où \(k=0,1,\dots,n\) sont identiquement nuls. La famille de polynômes \(\{\varphi_0\), \(\varphi_1\), \(\dots\), \(\varphi_n\}\) est donc linéairement indépendante (ou libre).
b)
Montrons maintenant que les polynômes \(\varphi_i\) forment une base de \(\mathbb{P}_n\). L'espace \(\mathbb{P}_n\) est un espace vectoriel de dimension \((n+1)\) et sa base canonique est \(1\), \(x\), \(x^2\), \(\dots\), \(x^n\). Comme les \((n+1)\) \(\varphi_i\) sont des polynômes de degré \(n\) linéairement indépendants, ils forment bien une base de \(\mathbb{P}_n\) : c'est la base de Lagrange associée aux noeuds \(x_0\), \(x_1\), \(\dots\), \(x_n\).
Le polynôme
\[ p(x) = \sum_{i=0}^{n}{p_i\varphi_i(x)} \]vérifie alors bien
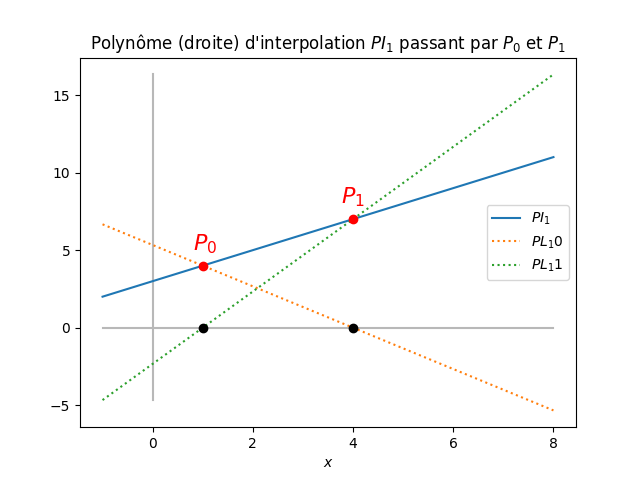
Exemple: Construisons le polynôme d'interpolation passant par les deux points \(P_0=(x_0=1,p_0=4)\) et \(P_1=(x_1=4,p_1=7)\). Pour ce faire, on écrit les deux polynômes constituant la base de Lagrange de \(\mathbb{P}_1\) : \[ \varphi_0(x) = \frac{x-x_1}{x_0-x_1} = \frac{x-4}{1-4} = \frac{4}{3}-\frac{x}{3} \]
et \[ \varphi_1(x) =\frac{x-x_0}{x_1-x_0} = \frac{x-1}{4-1} = \frac{x}{3}-\frac{1}{3}\,. \]
Le polynôme cherché est alors
\[ p(x) = p_0\varphi_0(x) + p_1\varphi_1(x) = 4\cdot\left(\frac{4}{3}-\frac{x}{3}\right) + 7\cdot\left(\frac{x}{3}-\frac{1}{3}\right) = \frac{16}{3} - \frac{4x}{3} + \frac{7x}{3}-\frac{7}{3} = x + 3\,. \] Ce polynôme \(p(x)\) est effectivement le seul polynôme de degré \(1\) (droite) passant par les deux points \(P_0\) et \(P_1\).
Dernière compilation: 2025-05-28 (06:27:05)
Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)
