La position angulaire d’une planète (ou d'une comète) se déplaçant autour du Soleil sur une orbite elliptique et le temps sont reliés par une équation appelée équation de Kepler :
\[ M = E - e\sin{E}\,, \]où \(M\) est l'anomalie moyenne (liée au temps), \(E\) est l'anomalie excentrique (liée à la position angulaire), et \(e\) est l'excentricité de la trajectoire. Une animation permettant de comprendre ce que sont les anomalies moyenne et excentrique peut être trouvée ici.
Connaissant la valeur de \(M\) et de \(e\), l'équation permet de déterminer \(E\), c'est-à-dire la position angulaire du corps autour du Soleil. Ainsi, la position de la comète de Halley lors de sa rencontre avec la sonde Giotto en 1986 a pu être déterminée en résolvant l'équation
\[ 0.0073673887 = E - 0.96727426\sin{E}\,, \]que l'on peut évidemment également mettre sous la forme
\[ f(E) = E - 0.96727426\sin{E} - 0.0073673887 = 0\,. \]Cette équation est non linéaire et ne possède pas de solution analytique. Pour l'étudier, on peut commencer par représenter graphiquement la fonction \(f(E)\). Comme le montrent les deux représentations suivantes, on constate ainsi visuellement que l'équation possède une seule solution et, en choisissant au mieux l'intervalle représenté, il est possible d'obtenir une première approximation ''visuelle'' de cette racine.
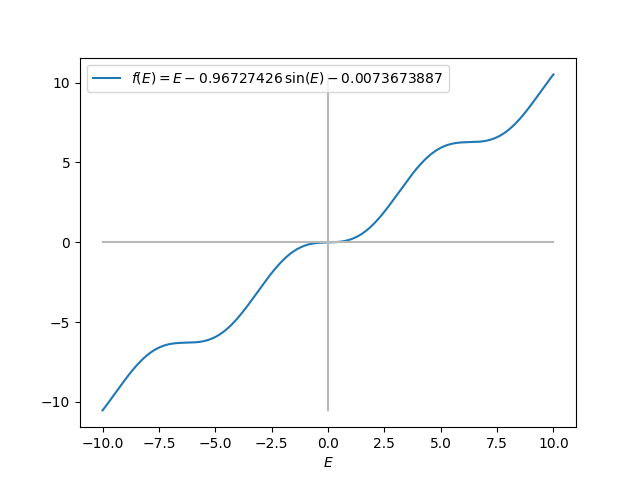
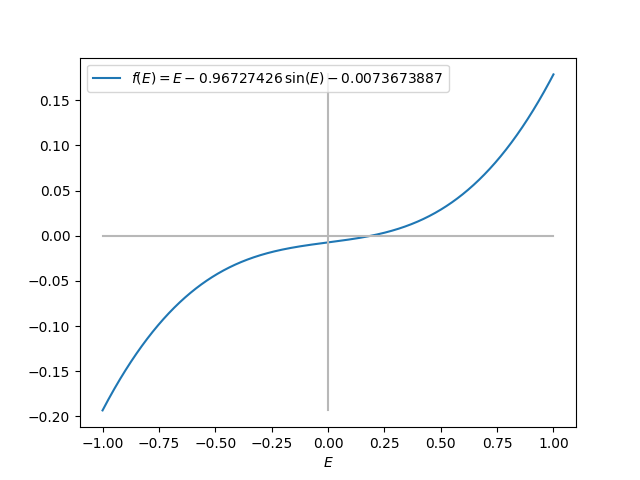
Les méthodes numériques décrites ci-dessous vont nous permettre d'affiner notre approche et de déterminer précisément la valeur de la racine cherchée.
Dernière compilation: 2025-05-28 (06:27:04)
Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)
