La méthode de la bissection est simple, mais ne garantit pas une réduction monotone de l'erreur d'une itération à l'autre. Pour obtenir des méthodes plus performantes, il est nécessaire de prendre davantage en compte les valeurs de la fonction \(f\), voire de considérer leur évolution par l'intermédiaire de la dérivée \(f'\) (si \(f\) est différentiable) ou par une approximation de cette dernière.
Il peut être utile de savoir approximer une fonction telle que \(\sin\) ou \(\cos\) par des polynômes. C'est ce qui a été fait en Analyse I au semestre d'automne en remplaçant par exemple \(\sin(x)\) par sa fonction infiniment petite équivalente (IPE) \(x\) au voisinage de \(x=0\) : \(\sin(x)\sim x\) au voisinage de \(x=0\). Durant le semestre de printemps, en Analyse II, vous allez poursuivre cette approche et obtenir le résultat important suivant (voir polycopié d'Analyse II, en page 66 et suivantes) :
Théorème:
(Théorème de Taylor ou Formule de Taylor).
Soient un intervalle ouvert \(I\subset \R\), un élément \(a\in I\), ainsi
qu'une fonction \(f:I\rightarrow \mathcal R\) continuement dérivable
en \(a\) jusqu'à un certain ordre \((n+1)\).
Alors pour tout nombre réel \(x\in I\), on peut écrire le
développement limité de \(f\) à l'ordre \(n\) autour de \(a\) :
\[\begin{aligned}
f(x) =& \,f(a) + \dfrac{f'(a)}{1!}(x-a) + \dfrac{f''(a)}{2!}(x-a)^2 + \dfrac{f'''(a)}{3!}(x-a)^3
+\ldots \\
& + \dfrac{f^{(n)}(a)}{n!}(x-a)^n + \dfrac{f^{(n+1)}(\xi)}{(n+1)!}(x-a)^{n+1} \\
=& \,\sum_{k=0}^{n}{\dfrac{f^{(k)}(a)}{k!}(x-a)^k} + \dfrac{f^{(n+1)}(\xi)}{(n+1)!}(x-a)^{n+1}\,,
\end{aligned}\]
où \(\xi\) est un nombre réel strictement compris entre \(a\) et \(x\).
Dans le développement ci-dessus, chaque terme fait intervenir la dérivée, à un certain ordre \(k\), évaluée en \(a\), de la fonction \(f\) :
\[ f^{(k)}(a) \equiv \frac{d^k}{dx^k}f(a)\,. \]La somme
\[ \sum_{k=0}^{n}{\dfrac{f^{(k)}(a)}{k!}(x-a)^k} \]est appelée polynôme de Taylor de la fonction \(f\) à l'ordre \(n\) autour de \(a\). On retrouve l'IPE de \(f\) en ne prenant que les premiers termes non nuls et non constants de cette somme.
Exemple:
Développement de Taylor de \(f(x)=sin(x)\) à l'ordre \(3\) au voisinage de \(a=0\) :
\[ sin(x) = x -\dfrac{x^3}{3!}+\dfrac{x^5}{5!}\cos{(\xi)}\,, \]où \(\xi\) est compris entre \(0\) et \(x\). Le dernière terme correspond au reste (c'est-à-dire à l'erreur commise si on s'arrête à l'ordre \(3\)). Par conséquent, en écrivant
\[ sin(x) \cong x -\dfrac{x^3}{3!}\,, \]l'erreur commise est d'au plus
\[ \dfrac{x^5}{5!}\cdot 1 = \dfrac{x^5}{120}\,. \]On note que le développement polynomial de \(f(x)=\sin{(x)}\) ne fait intervenir que des puissances impaires de \(x\), ce qui est cohérent avec le fait que le sinus est une fonction impaire.
Les méthodes de la sécante, de la corde et de Newton que nous allons discuter ci-dessous exploitent le développement limité au premier ordre de la fonction \(f\). Ecrivons le polynôme de Taylor au premier ordre au voisinage d'un point \(x_k\) (qui peut être la \(k\)ème approximation de la racine cherchée) :
\[ y(x) = f(x_k) + \frac{f'(x_k)}{1!} (x - x_k) \,. \]Cette fonction \(y\) est la tangente à la fonction \(f\) au point \(x_k\). En considérant cette fonction \(y\) comme une approximation de \(f\), il est naturel de chercher la racine de \(y\) et de la voir comme une approximation de la racine de \(f\). En appelant \(x_{k+1}\) cette racine de \(y\), il vient
\[\begin{aligned} y(x_{k+1}) =&\, f(x_k) + f'(x_k) (x_{k+1} - x_k) \\ =&\, 0\,. \end{aligned}\]Cette approche suggère la méthode itérative suivante :
\(\forall k\ge 0\), étant donné \(x_k\), déterminer \(x_{k+1}\) en résolvant l'équation
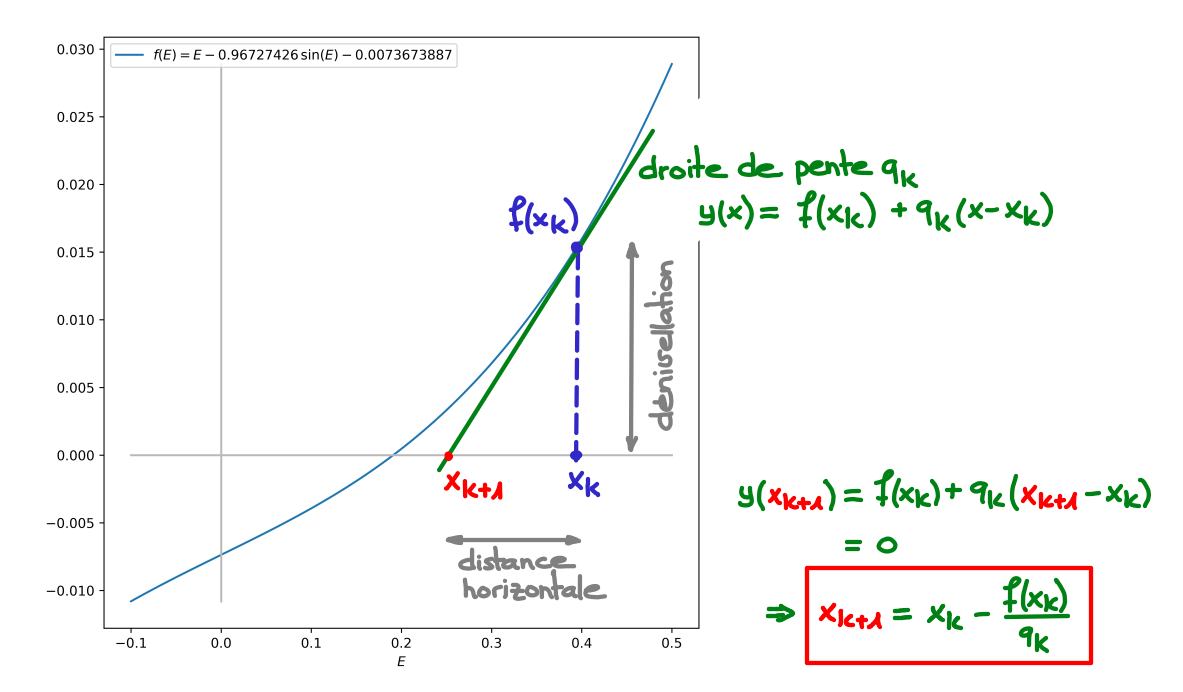
\[ f(x_k) + q_k (x_{k+1} - x_k) = 0 ~\Leftrightarrow~ x_{k+1} = x_{k} - \frac{f(x_k)}{q_k} \,, \]où \(q_k\) est la dérivée \(f'(x_k)\) de \(f\) évaluée en \(x_k\) ou une approximation de cette dernière. On est donc amené à chercher l'intersection \(x_{k+1}\) entre l'axe des \(x\) et la droite de pente \(q_k\) passant par le point \((x_k, f(x_k))\) :
Dans ce qui suit, nous allons considérer trois choix particuliers pour la pente \(q_k\).
Dans la méthode de la sécante, on se donne deux valeurs initiales \(x_{-1}\) et \(x_0\) qui peuvent, par exemple, être les bornes \(a\) et \(b\) de l'intervalle \([a,b]\) dans lequel on cherche une racine de \(f\).
On pose alors
\[ q_k = \frac{f(x_k) - f(x_{k-1})}{x_k-x_{k-1}}\,,~\forall k\ge 0\,. \]On a ainsi
\[ x_{k+1} = x_k - \underbrace{\frac {x_k-x_{k-1}}{f(x_k) - f(x_{k-1})}}_{=q_k^{-1}}f(x_k)\,,~\forall k\ge 0\,. \]Premières étapes de la méthode de la sécante :
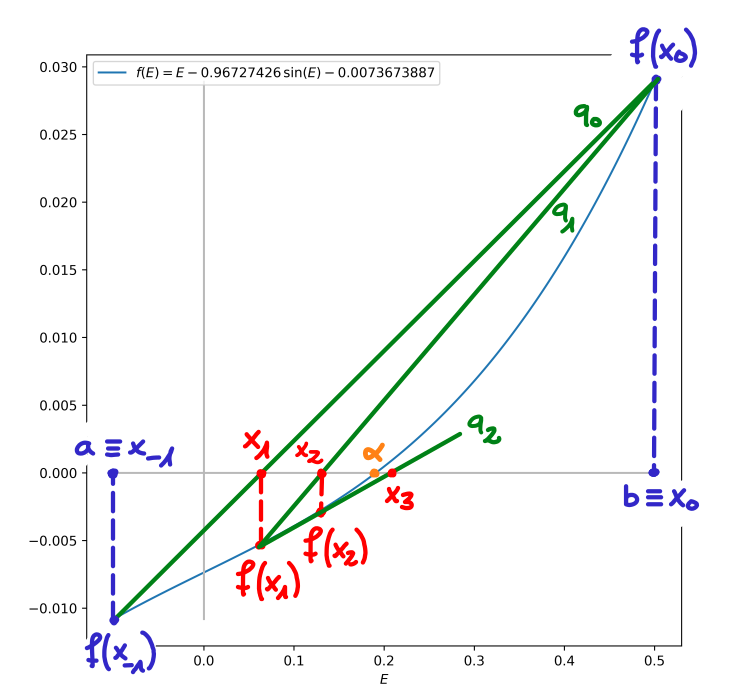
Les éléments de la suite \(\{x_k\}\) produite par la méthode de la sécante peuvent sortir de l'intervalle \([a,b]\) et même diverger. Toutefois, on peut montrer le résultat de convergence local suivant :
Théorème: Si \(f\in {\cal C}^2(J)\), où \(J\) est un voisinage de \(\alpha\), et si \(f'(\alpha)\ne 0\), et si \(x_{-1}, x_0\in J\) sont ''assez proches'' de \(\alpha\), l'ordre de convergence vers \(\alpha\) pour la méthode de la sécante est \[ p = \frac{1+\sqrt{5}}{2} \cong 1.618~\text{(nombre d'or)}. \]
Remarque: Le zéro \(\alpha\) est ici supposé être une racine simple de la fonction \(f\) : \(f(\alpha) = 0\) et \(f'(\alpha)\ne 0\).
Dans la méthode de la corde, on se donne une valeur initiale \(x_0\) et on utilise la même pente pendant tout le processus itératif en posant
\[ q_k = \frac{f(b)-f(a)}{b-a} \equiv q\,,~\forall k\ge 0\,. \]On a ainsi
\[ x_{k+1} = x_k - \underbrace{\frac {b-a}{f(b)-f(a)}}_{=q_k^{-1}\equiv q^{-1}}f(x_k)\,,~\forall k\ge 0\,. \]Premières étapes de la méthode de la corde :
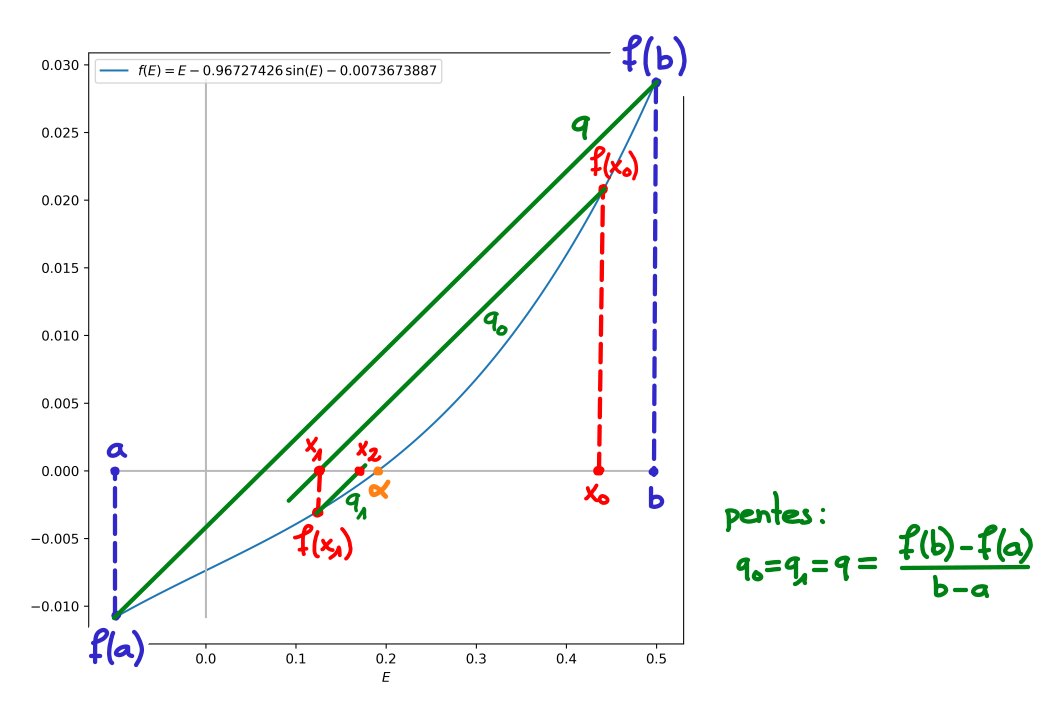
On peut montrer que la suite \(\{x_k\}\) converge avec un ordre de convergence \(p=1\).
La méthode de Newton nécessite que \(f\in{\cal C}^1(J)\). La fonction \(f\) doit donc être une fois continûment dérivable dans \(J\), \(J\) étant un voisinage ''suffisamment grand'' contenant \(\alpha\). De plus, on suppose que \(f'(\alpha)\ne 0\) (pour que la convergence soit optimale). Ces hypothèses étant vérifiées, on choisit une ''bonne'' première approximation \(x_0\) de \(\alpha\) et on pose
\[ q_k = f'(x_k)\,,\,\forall k\ge 0\,. \]On a ainsi
\[ x_{k+1} = x_k - \underbrace{\frac{1}{f'(x_k)}}_{=q_k^{-1}} f(x_k) = x_k - \frac{f(x_k)}{f'(x_k)}\,,\forall k\ge 0\,. \]Premières étapes de la méthode de Newton :
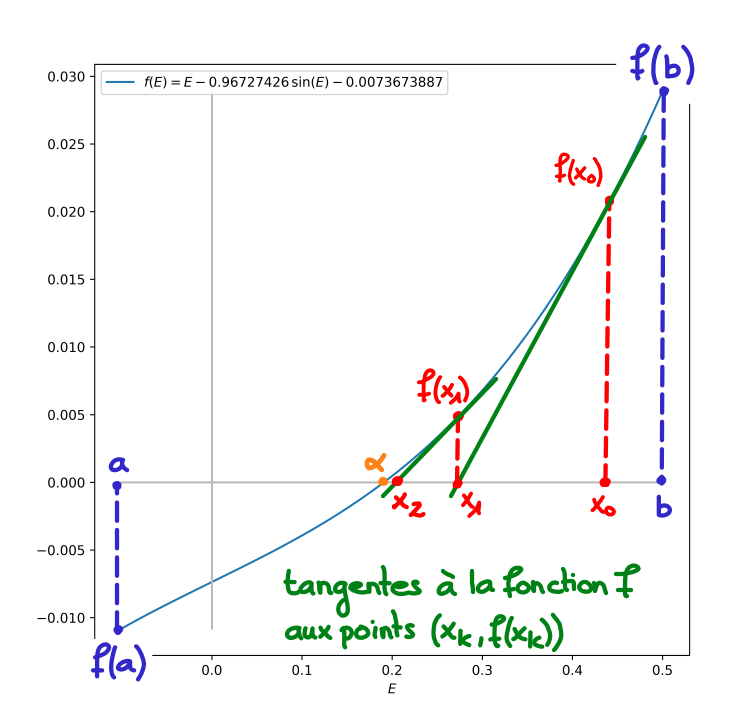
Géométriquement, \(x_{k+1}\) est l'abscisse du point d'intersection avec l'axe des abscisses de la tangente au graphe de \(f\) passant par le point \((x_k,f(x_k))\). La méthode de Newton est d'ailleurs également appelée méthode des tangentes (ou encore méthode de Newton-Raphson).
On montrera plus bas que la suite \(\{x_k\}\) converge avec un ordre de convergence \(p=2\). Remarquons que l'ordre de convergence de la méthode de Newton est \(p=1\) si \(f'(\alpha)=0\).
Dernière compilation: 2025-05-28 (06:27:04)
Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)
