Pour une fonction \(f:[a,b]\rightarrow \R\), il est toujours possible de transformer l'équation non linéaire à résoudre,
\[ f(x)=0\,, \]en une équation équivalente ayant les mêmes solutions :
\[ x-\Phi(x) = 0\,, \]où \(\Phi(x)\) est une fonction auxiliaire \(\Phi:[a,b]\rightarrow \R\) choisie telle que
\[ f(\alpha)=0~~\Rightarrow~~\alpha = \Phi(\alpha)\,. \]La recherche des zéros de \(f\) se ramène donc à la recherche des points fixes de \(\Phi\).
Remarque: Pour une fonction \(f\) donnée, le choix de la fonction auxiliaire \(\Phi\) n'est pas unique. Par exemple, on peut choisir \[ \Phi(x) = x + \lambda f(x)\,, \text{ où } \lambda\in\R\,. \]
En effet, pour cet ensemble de fonctions auxiliaires, on a \[ f(\alpha) = 0 ~\Rightarrow~ \Phi(\alpha) = \alpha + \lambda \underbrace{f(\alpha)}_{=0} = \alpha\,. \]
En effet, pour cet ensemble de fonctions auxiliaires, on a \[ f(\alpha) = 0 ~\Rightarrow~\Phi(\alpha) = \alpha + F(\underbrace{f(\alpha)}_{=0}) = \alpha + \underbrace{F(0)}_{=0} = \alpha\,. \]
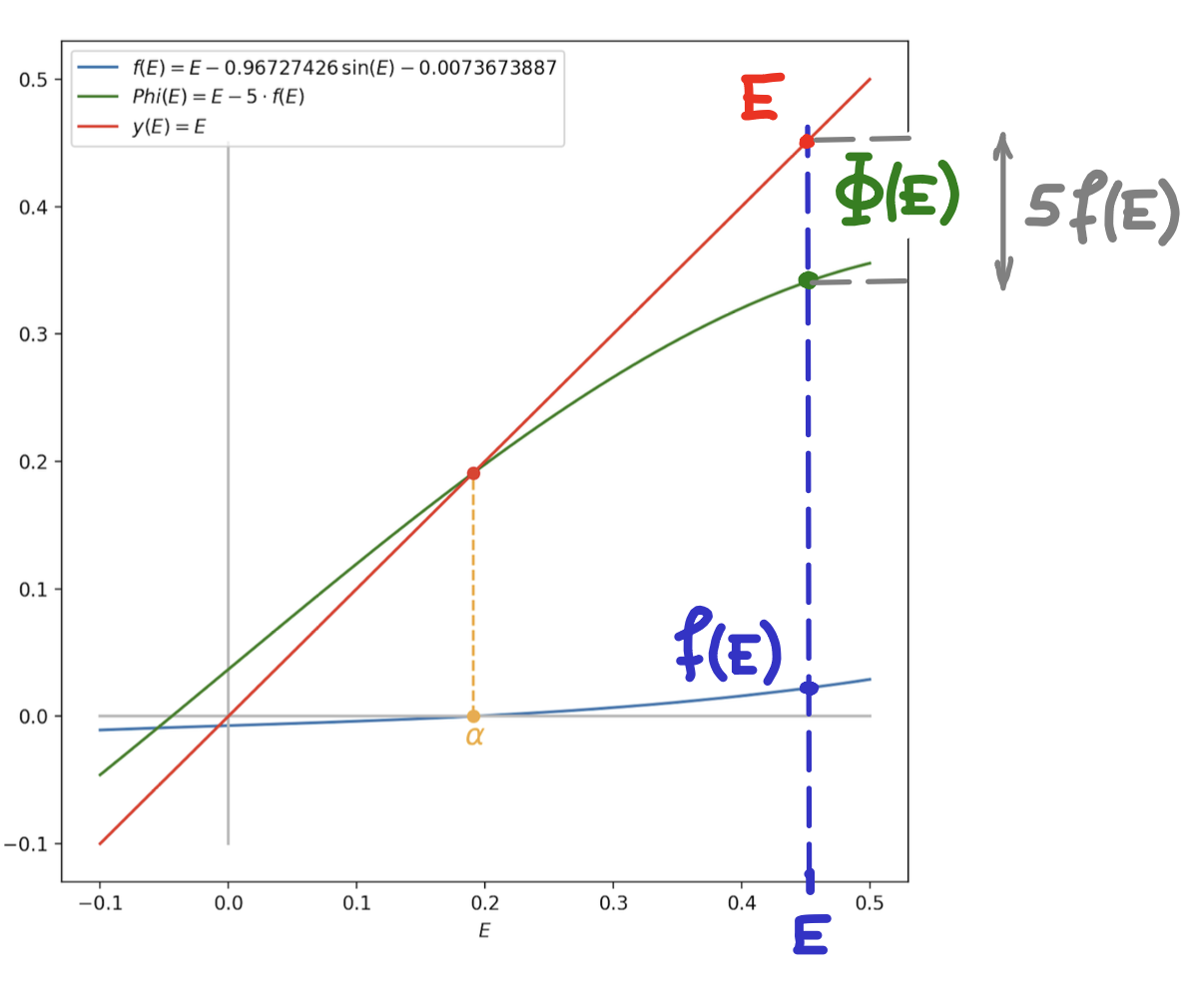
En guise d'exemple, nous allons transformer le problème de Kepler. Il est par exemple possible de choisir
\[ \Phi(E) = E -5f(E)\,. \]La racine de \(f\) et le point fixe de \(\Phi\) sont bien identiques.
Graphiquement, la recherche des points fixes de \(\Phi\) consiste à trouver la (ou les) intersection(s) entre la droite \(y(x)=x\) et la fonction \(y(x)=\Phi(x)\).
Dans la méthode de point fixe, le processus itératif revient à poser, étant donné un ''bon'' \(x_0\),
\[ x_{k+1} = \Phi(x_k)\,,~\forall k\ge 0\,. \]Cette relation est une itération de point fixe appelée parfois itération de Picard, et \(\Phi\) est connue sous le nom de fonction d'itération.
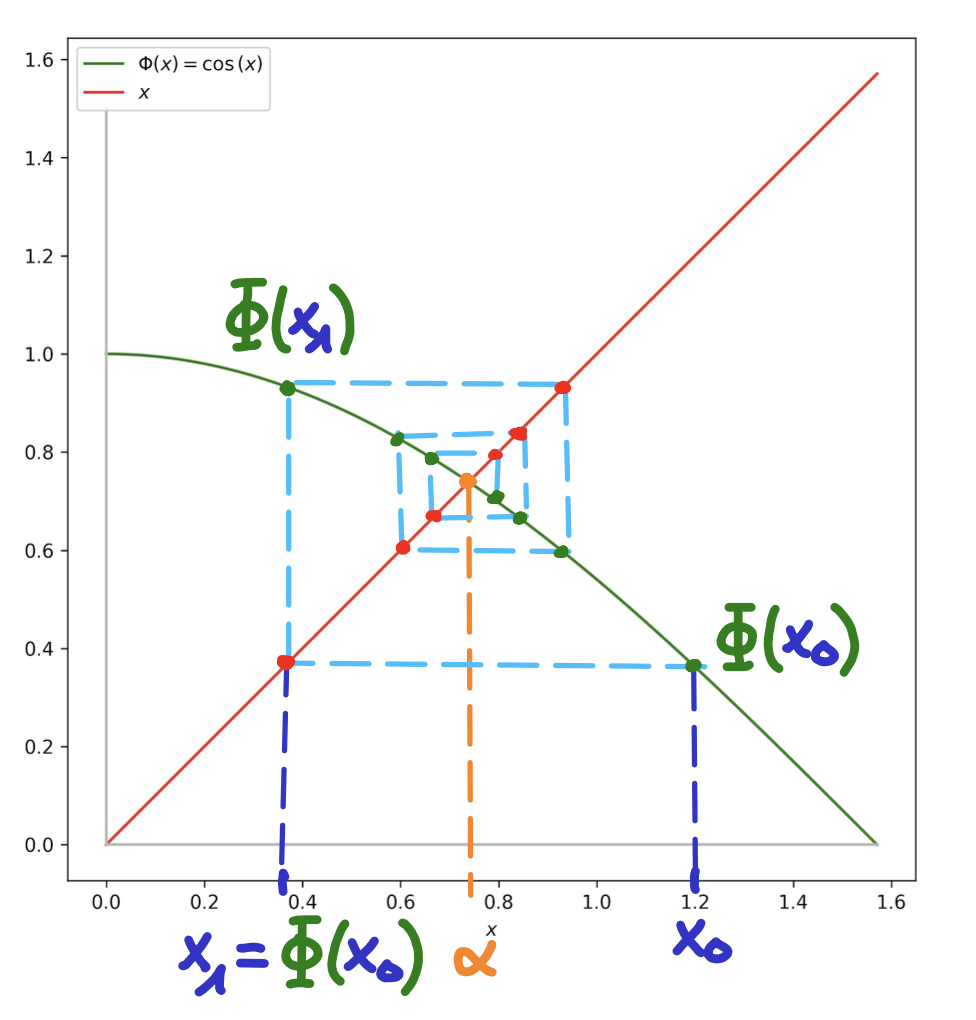
Premières étapes de la méthode pour la fonction d'itération \(\Phi(x) = \cos{(x)}\) :
\[\begin{aligned} x_0 =&~1.2 ~~~\text{ (choix du point de départ de la méthode)} \\ x_1 =&~\cos{(x_0)} = \cos{(1.2)} \cong 0.3624 \\ x_2 =&~\cos{(x_1)} \cong \cos{(0.3624)} \cong 0.9351 \\ x_3 =&~\cos{(x_2)} \cong \cos{(0.9351)} \cong 0.5938 \\ x_4 =&~\cos{(x_3)} \cong \cos{(0.5938)} \cong 0.8288 \\ x_5 =&~\cos{(x_4)} \cong \cos{(0.8288)} \cong 0.6757 \\ \vdots &~\\ x_{20} =&~\cos{(x_{19})} \cong \cos{(0.7388)} \cong 0.7393 \\ \vdots &~\\ x_{40} =&~\cos{(x_{39})} \cong \cos{(0.7391)} \cong 0.7391 \\ \end{aligned}\]Les toutes premières étapes sont représentées graphiquement ci-dessous :
Remarque:
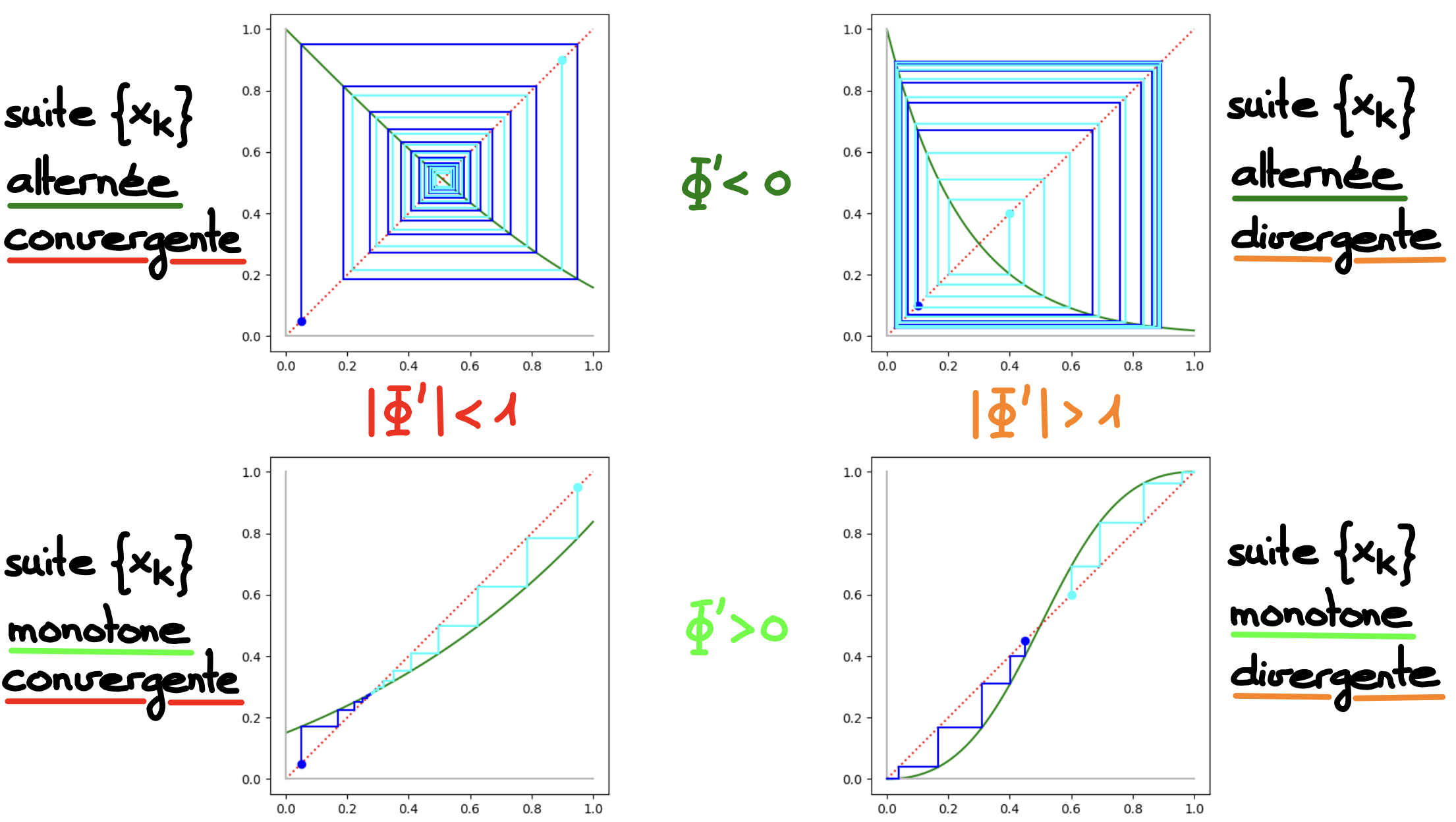
Comme le montrent certains des quatre exemples ci-dessous, la convergence de la méthode de point fixe n'est pas assurée. Elle dépend du choix de \(\Phi\) et de \(x_0\).
Application de la méthode de point fixe sur les fonctions \(f(x) = 1-\sin{(x)}\,,\) \(g(x) = \exp{(-4x)}\,, \) \(h(x) = 0.4 \exp{(x)}-0.25\, \) et \(i(x) = \displaystyle\frac{1}{1+\left(\frac{1-x}{x}\right)^2}\,, \) dans l'intervalle \(]0,1[\) :
Théorème: (existence d'un point fixe)
Soit \(\Phi\in{\cal C}^0([a,b])\), si \(\forall x\in[a,b]\), \(\Phi(x)\in [a,b]\),
Alors, \(\Phi\) admet au moins un point fixe \(\alpha\in [a,b]\).Nous allons considérer la fonction auxiliaire continue \(d : [a,b]\rightarrow \R\) définie par \(d(x) = \Phi(x) -x\), et nous intéresser au produit \(d(a)\cdot d(b)\) : \[ d(a)\cdot d(b) = \underbrace{(\Phi(a) -a)}_{\ge 0}\cdot \underbrace{(\Phi(b) -b)}_{\le 0}\le 0\,. \] Par le théorème de Bolzano, il existe au moins un \(\alpha\in [a,b]\) tel que \(d(\alpha )=0\) et \(\Phi(\alpha) = \alpha\).
Remarquons qu'en exploitant le théorème des accroissements finis (formule de Taylor au premier ordre), il vient, en supposant \(\Phi \in{\cal C}^1(I)\),
\[ |\Phi(x)-\Phi(y)| = |\Phi'(\xi)||x-y|\,, \]avec \(\xi\) entre \(x\) et \(y\). Par conséquent, on en déduit que si \(|\Phi'(x)| < 1\), \(\forall x\in I\), la fonction est \(K\)-contractante sur \(I\).
Les résultats suivants précisent les conditions qui doivent être satisfaites pour que la méthode de point fixe converge.
Théorème: Si la suite \(\{x_k\}\) définie par la méthode de point fixe converge vers \(x\) et si \(\Phi\) est continue, alors \(x\) est un point fixe de \(\Phi\).
\[ x = \lim_{k\rightarrow\infty}{x_{k+1}} = \lim_{k\rightarrow\infty}{\Phi(x_{k})} = \Phi(\lim_{k\rightarrow\infty}{x_{k}}) = \Phi(x)\,. \] On utilise successivement le fait que la suite converge, que \(x_{k+1}\) résulte d'une itération de point fixe, que \(\Phi\) est continue, et (encore une fois) que la suite converge.
Théorème: (théorème d'Ostrowski)
Soit \(\alpha\) un point fixe d'une fonction \(\Phi\in {\cal C}^{1}(J)\), où \(J\) est un voisinage de \(\alpha\). Si \(|\Phi'(\alpha)|\lt 1\), alors il existe \(\delta\gt 0\) pour lequel la suite \(\{ x_k\}\) converge vers \(\alpha\), pour tout \(x_0\) tel que \(|x_0-\alpha|\lt \delta\).
Théorème:
Soient \(x_0\) et la suite \(x_{k+1}=\Phi(x_k)\), \(\forall k\ge 0\).
Si
i) \(\forall x\in[a,b]\), \(\Phi(x)\in [a,b]\),
ii) \(\Phi\in{\cal C}^1([a,b])\),
iii) \(\exists K\lt 1 \text{ tel que } |\Phi'(x)|\lt K ~\forall x\in [a,b],\)
Alors \(\Phi\) a un unique point fixe \(\alpha\) dans \([a,b]\) et la suite \(\{x_k\}\) converge vers \(\alpha\) pour tout choix de \(x_0\in [a,b]\).
De plus, on a
\[ \lim_{k\rightarrow\infty}{\frac{x_{k+1}-\alpha}{x_k-\alpha}} = \Phi'(\alpha)\,. \]C'est un résultat de convergence globale : la suite converge vers \(\alpha\) avec un ordre 1 pour tout \(x_0\in[a,b]\).
Comme la fonction d'itération est continue et vérifie l'hypothèse i), cette dernière admet au moins un point fixe dans \([a,b]\) (voir la sous-section précédente).
Pour montrer l'unicité du point fixe, on va supposer qu'il existe deux valeurs \(\alpha_1\) et \(\alpha_2\) dans \([a,b]\) qui vérifient \(\Phi(\alpha_1)=\alpha_1\) et \(\Phi(\alpha_2)=\alpha_2\). La formule de Taylor à l'ordre 0 (c'est-à-dire le théorème des accroissements finis) et l'hypothèse de contraction iii) permettent alors d'écrire
\[ |\alpha_2 - \alpha_1| = |\Phi(\alpha_2)-\Phi(\alpha_1)|=|\Phi'(\xi)(\alpha_2-\alpha_1)|\le K|\alpha_2-\alpha_1|\lt |\alpha_2-\alpha_1|\,, \]où \(\xi\in\,]\alpha_1,\alpha_2[\,.\) On conclut que \(\alpha_1 = \alpha_2\).
L'étude de la convergence de la suite \(\{x_k\}\) peut également se faire à partir de la formule de Taylor. En effet, \(\forall k\ge 0\), on peut écrire
\[ x_{k+1} - \alpha = \Phi(x_{k})-\Phi(\alpha) = \Phi'(\xi_k)(x_k-\alpha)\,, \]avec \(\xi_k\) compris entre \(x_k\) et \(\alpha\). Il vient ainsi,
\[ |x_{k+1} - \alpha| = |\Phi'(\xi_k)||x_k-\alpha| \le K |x_k-\alpha|\le K^{k+1}|x_0-\alpha|\,. \]Or, \(\lim_{k\rightarrow\infty}{K^{k+1}|x_0-\alpha|} = 0\) et on conclut que \(x_k\) converge vers \(\alpha\).
En reprenant l'égalité \(x_{k+1} - \alpha = \Phi'(\xi_k)(x_k-\alpha)\) à la lumière de cette convergence, on termine la preuve :
\[ \lim_{k\rightarrow\infty}{\frac{x_{k+1} - \alpha}{x_k-\alpha}} = \lim_{k\rightarrow\infty}{\Phi'(\xi_k)}=\Phi'(\alpha)\,. \]La méthode de Newton,
\[ x_{k+1} = x_k - \frac{f(x_k)}{f'(x_k)} \equiv \Phi_{\text{N}}(x_k)\,, \]est une méthode de point fixe ayant pour fonction d'itération la fonction
\[ \Phi_{\text{N}}(x) = x - \frac{f(x)}{f'(x)}\,. \]On note que la dérivée de cette fonction d'itération s'annule au point correspondant à la racine \(\alpha\) de \(f\) : \(\Phi_{\text{N}}'(\alpha) = 0\). En effet,
\[ \Phi_{\text{N}}'(x) = 1 - (f(x)f'(x)^{-1})' = 1-\frac{f'(x)}{f'(x)} + \frac{f(x)f''(x)}{(f'(x))^2} = \frac{f(x)f''(x)}{(f'(x))^2}\,, \]et on a donc \(\Phi_{\text{N}}'(\alpha) = 0\) car \(f(\alpha)=0\) et \(f'(\alpha)\ne 0\). Ainsi, \(|\Phi_{\text{N}}'(\alpha)|\lt 1\), et la méthode converge.
De plus, en utilisant la formule de Taylor à l'ordre \(1\) au voisinage de \(\alpha\), il vient
\[\begin{aligned} x_{k+1} - \alpha =& ~\Phi_{\text{N}}(x_k) - \Phi_{\text{N}}(\alpha) \\ =& ~\left[ \Phi_{\text{N}}(\alpha) + \Phi_{\text{N}}'(\alpha)(x_k-\alpha)+\frac{\Phi_{\text{N}}''(\xi)(x_k-\alpha)^2}{2!} \right]\\ &~~-\Phi_{\text{N}}(\alpha)\,. \end{aligned}\]Comme \(\Phi_{\text{N}}'(\alpha) = 0\), on obtient finalement
\[ x_{k+1} - \alpha = \Phi_{\text{N}}(x_k) - \Phi_{\text{N}}(\alpha) = \frac{\Phi_{\text{N}}''(\xi)(x_k-\alpha)^2}{2!} \,. \]Ainsi,
\[ |x_{k+1}-\alpha| \le C |x_k-\alpha|^2\,, \]où
\[ C = \max_{\text{voisinage de }\alpha}\left|\frac{\Phi''_{\text{N}}(x)}{2}\right|\,. \]La convergence de la méthode de Newton est donc bien quadratique (\(p=2\)).
Dernière compilation: 2025-05-28 (06:27:04)
Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)
