ICS CMS | R. Sauser (EPFL)

3.1 Introduction

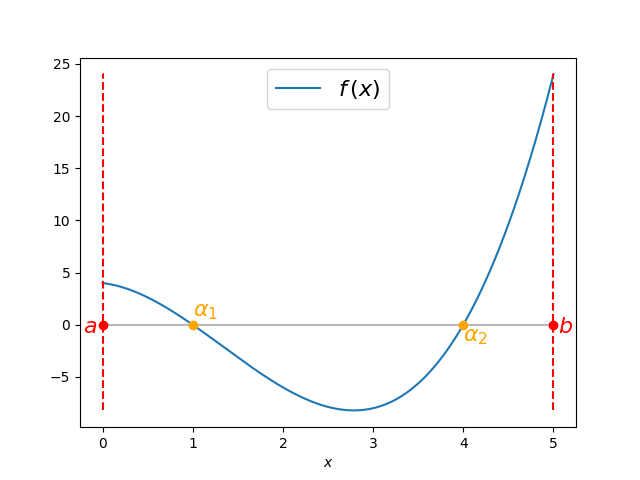
Dans ce chapitre, on se propose de déterminer, de manière approchée, la ou les racine(s) (zéro(s)) d'une fonction continue. Autrement dit, soit une fonction continue \(f:I=[a,b]\subset \R\rightarrow\R\), on cherche à déterminer la (ou les) valeur(s) \(\alpha\in I\) telle(s) que

\[ f(\alpha)=0\,. \]

Un nombre \(\alpha\) tel que \(f(\alpha)=0\) est un zéro (ou une racine) de la fonction \(f\).

L'idée consiste à envisager une méthode itérative permettant de construire une suite \(\{x_k\}\), \(k\in\N\), telle que \(\lim_{k\rightarrow \infty}{x_k}=\alpha\). Le premier élément de la suite, \(x_0\), peut par exemple être une approximation obtenue visuellement en représentant la fonction \(f\).

En pratique, numériquement, il est impossible d'effectuer une infinité d'itérations. La méthode fournira donc une solution approchée obtenue après un nombre fini d'itérations.

On dit qu'une telle suite \(\{x_k\}\), \(k\in\N\), converge avec un ordre \(p\ge 1\) s'il existe une constante \(C\gt 0\) telle que \[ |x_{k+1}-\alpha| \le C |x_{k}-\alpha|^p \,,\forall k\ge k_0\,, \text{ où } k_0\ge 0\text{ est un entier}. \] Remarquons que si \(p=1\), il faut que \(C\lt 1\) pour que \(x_k\) converge vers \(\alpha\).

La différence entre la solution approchée \(x_k\) obtenue après un nombre fini \(k\) d'itérations et la racine \(\alpha\) représente l'erreur numérique \(e_k\). Cette erreur numérique est la somme des erreurs de troncature et d'arrondi.

L'erreur numérique (absolue), notée \(e_k\) ou \(e_{k,\text{abs}}\), est définie par \[ e_k = |x_k-\alpha|\,. \]

L'erreur numérique relative est définie par \[ e_{k,\text{rel}} = \frac{|x_k-\alpha|}{|\alpha|}\,, \text{ si }\alpha\neq 0\,. \]