Théorème:
(Théorème des valeurs intermédiaires).
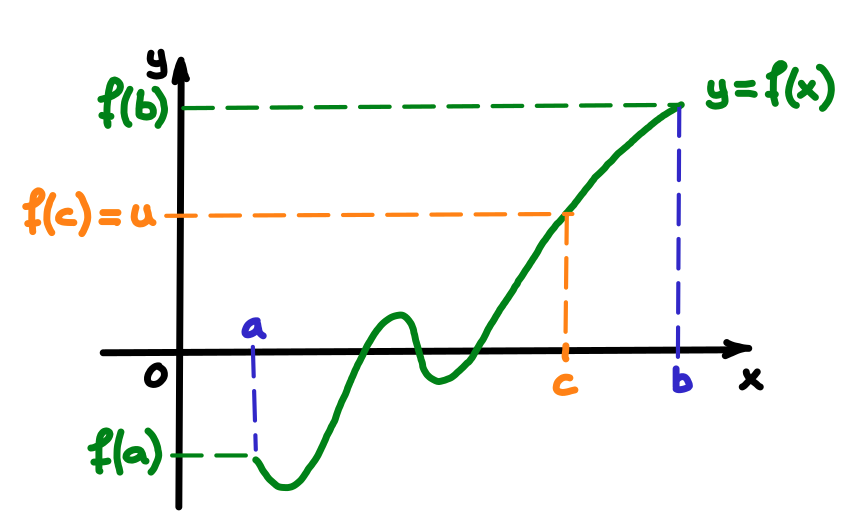
Soit une fonction continue \(f:I=[a,b]\subset \R\rightarrow\R\),
soit \(u\in\R\), \(u\) compris entre \(f(a)\) et \(f(b)\),
alors
\[
\exists\, c\in\R, c\in \,]a,b[ \text{ tel que } f(c)=u\,.
\]
Le mot dichotomie vient du grec dikhotomia qui signifie ''division en deux parties''. Une méthode de dichotomie est une méthode dans laquelle on met en ''opposition'' deux sous-intervalles.
Dans la méthode de la bissection, à chaque itération, on est amené à choisir entre deux sous-intervalles. Ce choix se base sur le théorème de Bolzano qui est un cas particulier du théorème des valeurs intermédiaires.
Théorème:
(Théorème des valeurs intermédiaires).
Soit une fonction continue \(f:I=[a,b]\subset \R\rightarrow\R\),
soit \(u\in\R\), \(u\) compris entre \(f(a)\) et \(f(b)\),
alors
\[
\exists\, c\in\R, c\in \,]a,b[ \text{ tel que } f(c)=u\,.
\]

Théorème:
(Théorème de Bolzano).
Soit une fonction continue \(f:I=[a,b]\subset \R\rightarrow\R\),
si \(f(a) f(b) \lt 0\),
alors
\[
\exists\, \alpha\in\R, \alpha\in \,]a,b[ \text{ tel que } f(\alpha)=0\,.
\]
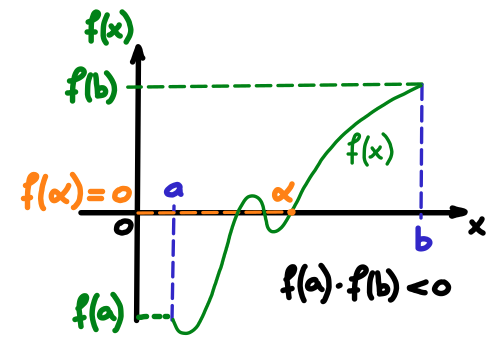
Le théorème de Bolzano a été appelé théorème de la valeur intermédiaire en Analyse I au semestre d'automne.
Dans la méthode de la bissection, on commence par s'assurer que l'hypothèse \(f(a)f(b)\lt 0\) du théorème de Bolzano est bien vérifiée pour l'intervalle de départ \(I_0=[a,b]\) considéré. On sait alors que \(I_0\) contient une racine \(\alpha\). On choisit de prendre comme première approximation de cette racine le point milieu de \(I_0\), c'est-à-dire le point \[ x_0=\frac{a+b}{2}\,. \] Si \(f(x_0) = 0\), on a trouvé une racine de \(f\). Sinon, on choisit parmi les deux sous-intervalles (identiques) définis par \(a\), \(x_0\) et \(b\), celui qui contient nécessairement une racine :
On itère alors en prenant comme nouvelle approximation de \(\alpha\) le milieu de \(I_1\). Et ainsi de suite. La figure suivante permet de visualiser concrètement les premières itérations de la méthode de la bissection :
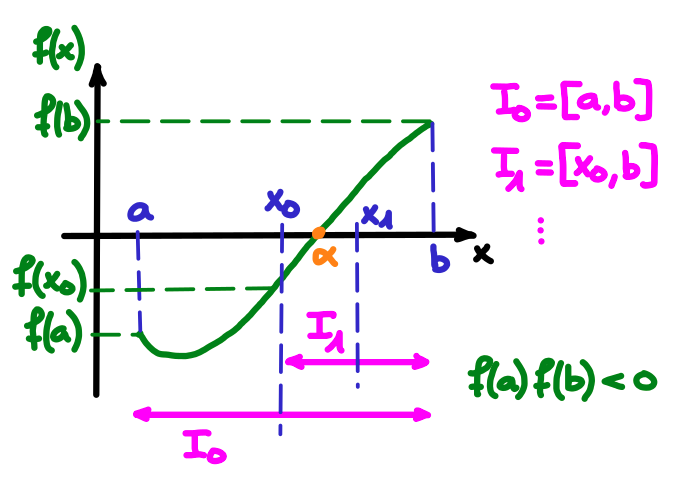
Dans la méthode de la bissection, la longueur des intervalles devient de plus en plus petite, \(\lim_{k\rightarrow\infty}{|b_k-a_k|=0}\), et les valeurs \(x_k\) fournissent des approximations de plus en plus précises de la racine \(\alpha\). Souvent, on termine la méthode quand l'intervalle considéré à une étape \(m\) est plus petit qu'une certaine tolérance (précision) \(\varepsilon\) que l'on aimerait atteindre :
\[ |x_m - \alpha| \le |I_m| \le \varepsilon\,, \]où \(|I_m|\equiv |b_m-a_m|\) représente la longueur de l'intervalle \(I_m\).
Intéressons-nous à l'erreur absolue commise à l'étape \(k\) en se souvenant qu'à chaque étape la longueur de l'intervalle est divisée par deux :
\[ e_k = |x_k -\alpha| \lt \frac{1}{2} |b_k-a_k| = \frac{1}{2} \frac{1}{2^k} |b_0-a_0| = \frac{1}{2^{k+1}}|b-a| \xrightarrow{k\rightarrow \infty} 0\,. \]Pour s'assurer que \(e_k \lt \varepsilon\), avec \(\varepsilon\) la tolérance souhaitée, le nombre minimal d'itérations à effectuer est donc :
\[ k_{\text{min}} \gt \log_2\left(\frac{|b-a|}{\varepsilon}\right)-1\,. \]Dans cette expression, la fonction \(\log_2\) est la fonction réciproque de la fonction puissance de \(2\).
Remarques:
Si la fonction \(f\) possède plusieurs zéros sur l'intervalle \([a,b]\), on commence souvent par découper \([a,b]\) en un certain nombre (suffisant) de sous-intervalles pour appliquer ensuite sélectivement la méthode de la bissection sur chacun des sous-intervalles intéressants, c'est-à-dire sur chaque sous-intervalles contenant un zéro par la condition de Bolzano. On appelle cette technique méthode de la bissection par intervalles. Nous allons l'utiliser dans l'exercice 1 de la série 15.
Le code Python suivant permet de résoudre l'équation de Kepler avec une tolérance \(\varepsilon = 10^{-8}\) à l'aide de la méthode de la bissection :
import numpy as np
def f(E):
return E - 0.96727426*np.sin(E) - 0.0073673887
a = 0
b = 0.5
eps = 1e-8
compteur_iterations = 0
point_milieu = (a + b)/2
if f(a)*f(b) >= 0:
print("L'intervalle [a,b] n'est pas approprié !")
else:
while (b - a)/2 > eps:
if f(a)*f(point_milieu) < 0:
a = a
b = point_milieu
point_milieu = (a + b)/2
compteur_iterations += 1
elif f(point_milieu)*f(b) < 0:
a = point_milieu
b = b
point_milieu = (a + b)/2
compteur_iterations += 1
elif f(point_milieu) == 0:
print('La solution obtenue est exacte !')
break
else:
print("Le zéro n'a pas pu être approché.")
break
print(f"L'approximation de la racine cherchée est alpha = {point_milieu}.")
print(f"Elle a été obtenue après {compteur_iterations} itérations.")
L'approximation de la racine cherchée est alpha = 0.19091079384088516.
Elle a été obtenue après 25 itérations.
En représentant l'écart \(|x_k-\alpha|\) entre solution approchée et solution exacte en fonction du nombre \(k\) d'itérations, on constate, sans surprise, que l'erreur n'est pas réduite de façon monotone d'une itération à l'autre. On ne peut donc effectivement pas définir d'ordre de convergence pour la méthode de la bissection.
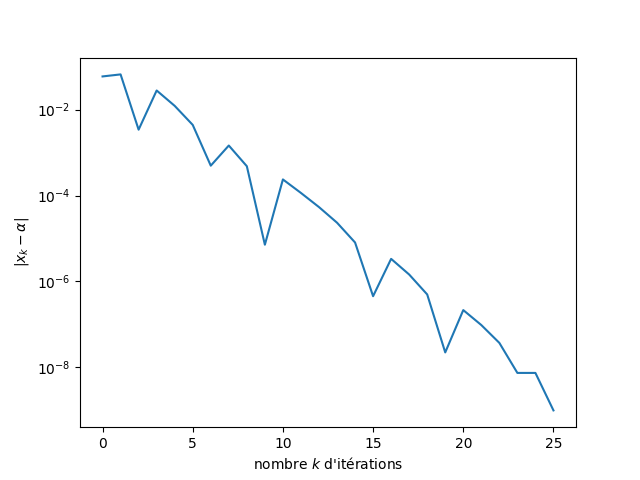
Remarquons que, comme la solution exacte n'est pas connue, cette représentation a été obtenue en posant \(\alpha = x_{25}\).