On parle ici de résidu car \(f(\alpha)=0\).
Le processus itératif est arrêté dès que \(|f(x_k)|\lt \varepsilon\), où \(\varepsilon\) est la tolérance fixée.
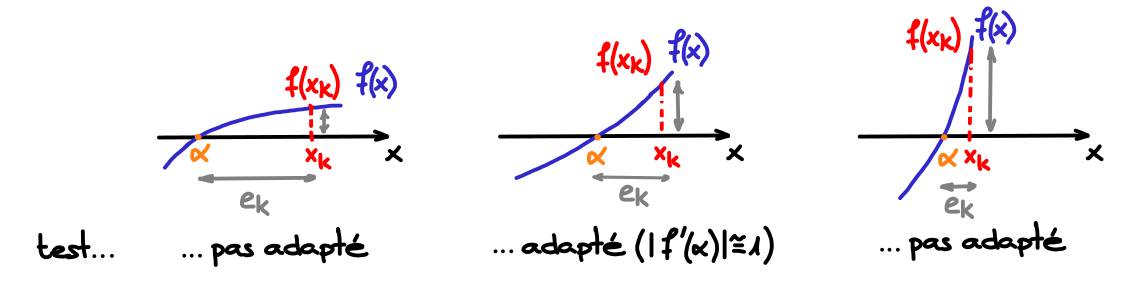
Ce test donne une bonne indication de l'erreur commise lorsque \(|f'(\alpha )|\cong 1\), c'est-à-dire lorsque la fonction varie de manière plus ou moins identique en abscisse et en ordonnée dans un voisinage de \(\alpha\) : on a alors \(|x_k-\alpha|\cong \varepsilon\).
Le processus itératif est arrêté dès que \(|x_{k+1}-x_k|\lt \varepsilon\).
Remarquons que dans le cas d'une méthode de point fixe avec une fonction d'itération \(\Phi(x)\) ce test n'est pas satisfaisant si \(\Phi'(\alpha )\) est proche de \(1\).
En effet, en exploitant le théorème des accroissements finis, c'est-à-dire la formule de Taylor à l'ordre zéro, il vient \[ x_{k+1}-\alpha = \Phi(x_k)-\Phi(\alpha) = \Phi'(\xi)(x_k-\alpha)\,, \] avec \(\xi\) entre \(x_k\) et \(\alpha\). Or, \[\begin{aligned} x_{k}-\alpha =&~ (x_{k+1}-\alpha) + (x_{k}-x_{k+1}) \\ =&~ \Phi'(\xi)(x_k-\alpha)+ (x_{k}-x_{k+1})\,. \end{aligned}\] Ainsi, \[ x_{k}-\alpha = \frac{1}{1-\Phi'(\xi)} (x_{k}-x_{k+1})\,. \] Dans le cas où \(\Phi'(\alpha )\) est proche de \(1\), un incrément petit ne permet pas d'assurer que les valeurs de la suite sont proches de la racine cherchée.
