ICS CMS | R. Sauser (EPFL)

7.3 Méthodes numériques à un pas

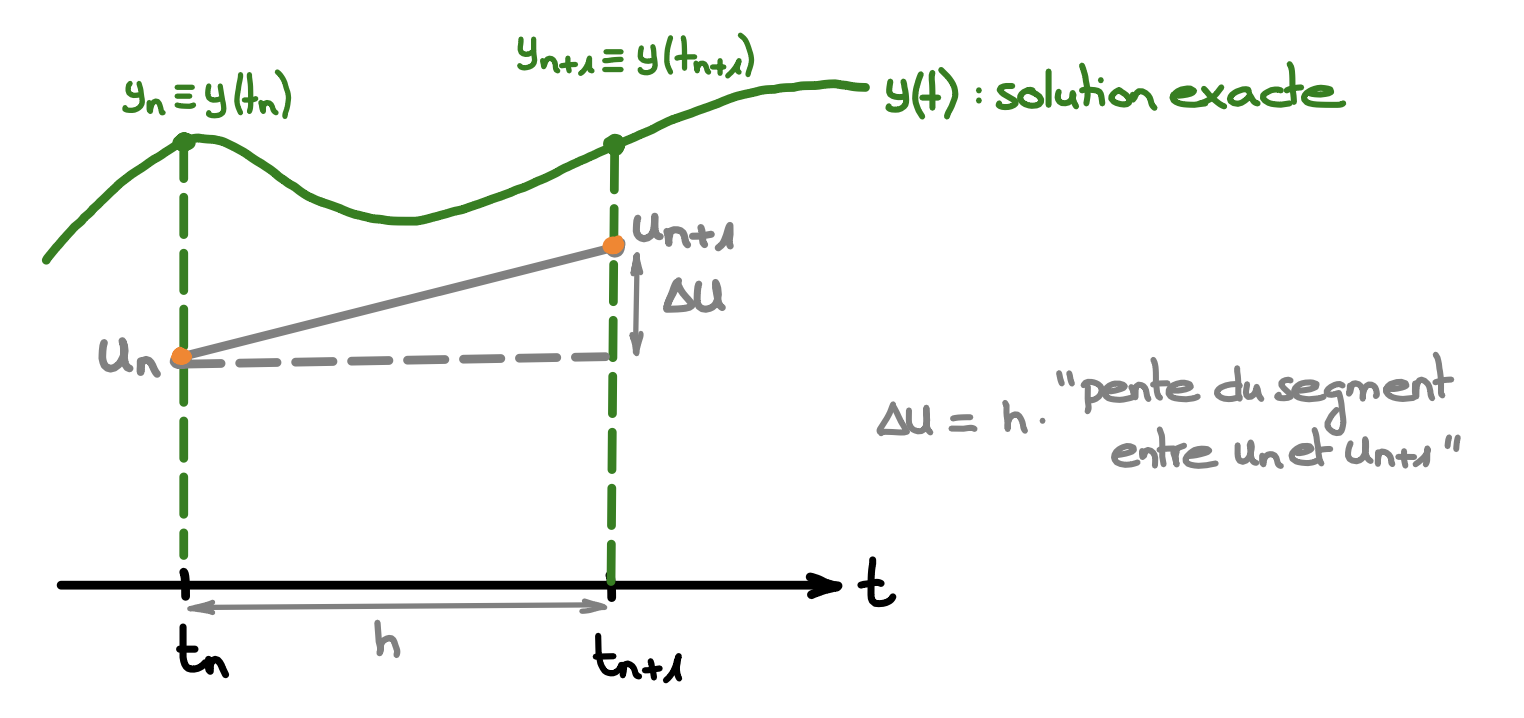
Le déroulement d'une méthode numérique à un pas est le suivant :

On choisit une partition régulière de \(I=[t_0,T]\) : \(t_0\lt t_1\lt t_2\lt\dots\lt t_N=T\), où \(N\) est le nombre de sous-intervalles et \(h=\frac{T-t_0}{N}\) est le pas de discrétisation.
Pour chacun des noeuds \(t_n=t_0+nh\,,\) avec \(1\le n\le N\), on cherche la valeur inconnue \(u_n\) qui approche \(y_n\equiv y(t_n)\). L'ensemble des valeurs \(\{u_0\equiv y_0, u_1,u_2,\dots,u_N\}\), construit à partir de la condition initiale \(u_0\equiv y_0\), représente la solution numérique.
On repète éventuellement la méthode en considérant des partitions de plus en plus fines, c'est-à-dire des partitions avec des pas \(h\) de plus en plus petits.

Pour chaque sous-intervalle \([t_n,t_{n+1}]\), on a l'égalité

\[ y_{n+1} = y_n + \int_{t_n}^{t_{n+1}}{f(t,y(t))dt}\,. \]

La méthode numérique choisie permet d'obtenir une approximation de l'intégrale donnant \(y_{n+1}\equiv y(t_{n+1})\) à partir de \(y_n\equiv y(t_n))\). Nous allons envisager six manières de calculer numériquement cette intégrale.

Chacune de ces méthodes permet d'obtenir, pour chaque instant \(t_{n+1}\) avec \(n=0,\ldots,N-1\), c'est-à-dire pour chaque noeud de la partition de pas \(h\) choisie, une approximation numérique \(u_{n+1}\) de \(y_{n+1}\) :

\[u_0\equiv y_0 \longrightarrow u_1 \longrightarrow u_2\longrightarrow\ldots \longrightarrow u_n \longrightarrow u_{n+1}\]

On obtient l'approximation \(u_{n+1}\) en \(t_{n+1}\) en partant de l'approximation \(u_n\) en \(t_n\) :

\[ u_{n+1} = u_n + \Delta u\,, \]

où \(\Delta u\) n'est autre que la ''pente'' choisie multipliée par le pas \(h\).

Méthode d'Euler progressive

Dans la méthode d'Euler progressive, on choisit d'approcher numériquement l'intégrale définie \[ \int_{t_n}^{t_{n+1}}{f(t,y(t))dt} \] à l'aide de la formule de quadrature non composite du point de gauche :

\[ J_n^{\text{PG}}(f) = \underbrace{(t_{n+1}-t_n)}_{=h}f(t_n,y(t_n))\,. \]

En remplaçant \(y(t_n)\), dont la valeur est inconnue, par l'approximation \(u_n\), on obtient alors le schéma numérique suivant :

\[ \left\{\begin{array}{rcl} u_{n+1} &=& u_n + hf_n\,,\\ u_0&=&y_0\,.\end{array}\right. \]

où \(f_n=f(t_n,u_n)\).

Dans cette méthode, la ''pente'' \(\Delta u/h\) choisie est

\[ f_n\equiv f(t_n,u_n) \]

\[ u_{n+1} = u_n + \Delta u = u_n+hf_n = u_n+h f(t_n,u_n)\,. \]

Méthode d'Euler rétrograde

Dans la méthode d'Euler rétrograde, on approche numériquement l'intégrale définie

\[ \int_{t_n}^{t_{n+1}}{f(t,y(t))dt} \]

à l'aide de la formule de quadrature non composite du point de droite :

\[ J_n^{\text{PD}}(f) = \underbrace{(t_{n+1}-t_n)}_{=h}f(t_{n+1},y(t_{n+1}))\,. \]

On obtient alors le schéma numérique suivant :

\[ \left\{\begin{array}{rcl} u_{n+1} &=& u_n + hf_{n+1}\,,\\ u_0&=&y_0\,.\end{array}\right. \]

Cette méthode est implicite car \(f_{n+1}=f(t_{n+1},u_{n+1})\). Ainsi, on est finalement amené à rechercher le point fixe de l'équation

\[ u_{n+1} = u_n + hf_{n+1} = g(u_{n+1}) \,. \]

Dans cette méthode, la ''pente'' \(\Delta u/h\) choisie est

\[ f_{n+1}\equiv f(t_{n+1},u_{n+1}) \]

\[ u_{n+1} = u_n + \Delta u = u_n+hf_{n+1} = u_n+h f(t_{n+1},u_{n+1})\,. \]

Ici, pour obtenir l'approximation \(u_{n+1}\), on est donc naturellement amené à résoudre une équation par la méthode de point fixe :

\[ u_{n+1} = u_n + hf_{n+1} = g(u_{n+1}) \,. \]

C'est ce que l'on fait par exemple à l'exercice 2 de la série 23. Il est également possible de résoudre cette équation par une autre méthode de recherche de zéros (voir par exemple l'exercice 3 de la série 23 dans lequel on utilise la fonction newton de SciPy).

Méthode de Crank-Nicolson

Dans la méthode de Crank-Nicolson, on approche numériquement l'intégrale définie à l'aide de la formule de quadrature non composite du trapèze :

\[ J_n^{\text{TR}}(f) = \underbrace{(t_{n+1}-t_n)}_{=h}\dfrac{f(t_{n},y(t_{n})) +f(t_{n+1},y(t_{n+1}))}{2}\,. \]

On obtient alors le schéma numérique implicite suivant :

\[ \left\{\begin{array}{rcl} u_{n+1} &=& u_n + \dfrac{h}{2}(f_n+f_{n+1})\,,\\ u_0&=&y_0\,.\end{array}\right. \]

La nature implicite de cette méthode rend cette dernière difficile à mettre en place. Souvent, on utilise plutôt un schéma légèrement modifié grâce à une approche de type ''prédicteur-correcteur'' : on commence par faire une prédiction, c'est-à-dire un premier calcul, par exemple à l'aide du schéma d'Euler (progressif), pour obtenir une approximation

\[ u_{n+1}^*=u_n+hf_n\,. \]

La valeur inconnue \(f_{n+1}\) est alors remplacée par

\[ f_{n+1}^*=f(t_{n+1},u_{n+1}^*)\,. \]

En procédant ainsi, on obtient la méthode de Heun décrite ci-dessous.

Méthode de Heun

Directement inspirée de la méthode de Crank-Nicolson, la méthode de Heun est une méthode explicite correspondant au schéma suivant :

\[ \left\{\begin{array}{rcl} u_{n+1} &=& u_n + \dfrac{h}{2}(f_n+f_{n+1}^*)\,,\\ u_0&=&y_0\,.\end{array}\right. \]

Il s'agit d'une méthode (de Runge-Kutta) explicite en deux étapes :

\[ \begin{array}{rcl} K_1 &=& f(t_n,u_n)\,,\\ K_2 &=&f(t_{n+1},u_n+hK_1)\,,\end{array} \]

où \(K_1\) et \(K_2\) sont les deux pentes importantes dans la méthode.

Ainsi, le schéma peut être réécrit de la façon suivante :

\[ \left\{\begin{array}{rcl} u_{n+1} &=& u_n + \dfrac{h}{2}(K_1+K_{2})\,,\\ u_0&=&y_0\,.\end{array}\right. \]

Méthode d'Euler modifiée (améliorée)

On peut également envisager approcher numériquement l'intégrale du problème de Cauchy à l'aide de la formule de quadrature non composite du point milieu :

\[ J_n^{\text{PM}}(f) = hf(t_{n}+\frac{h}{2},y(t_{n}+\frac{h}{2}))\,. \]

Comme on ne connaît pas \(u_{n+1/2}\), on exploite souvent la méthode d'Euler (progressive) pour écrire :

\[ u_{n+1/2} = u_n + \frac{h}{2}f_n\,. \]

On obtient alors un schéma appelé méthode d'Euler modifiée (améliorée) :

\[ \left\{\begin{array}{rcl} u_{n+1} &=& u_n + hf_{n+1/2}\,,\\ u_0&=&y_0\,,\end{array}\right. \]

où \(f_{n+1/2} = f(t_n+\frac{h}{2}, u_{n+1/2})\). On appelle également cette méthode la méthode de Runge-Kutta ''classique'' à deux étapes :

\[ \begin{array}{rcl} K_1 &=& f(t_n,u_n)\,,\\ K_2 &=&f(t_{n}+\frac{h}{2},u_n+\dfrac{h}{2}K_1)\,.\end{array} \] Ainsi, le schéma peut être réécrit de la façon suivante :

\[ \left\{\begin{array}{rcl} u_{n+1} &=& u_n + hK_2\,,\\ u_0&=&y_0\,.\end{array}\right. \]

Méthode classique de Runge-Kutta

Notre étude de l'intégration numérique suggère que l'on peut également envisager utiliser la formule de quadrature non composite de Simpson :

\[ J_n^{\text{S}}(f) = \frac{h}{6} \left[ f(t_{n},y(t_{n})) + 4 f(t_{n}+\frac{h}{2},y(t_{n}+\frac{h}{2})) + f(t_{n+1},y(t_{n+1})) \right]\,. \]

La méthode de Runge-Kutta classique (à 4 étapes) RK4 consiste à prendre (il s'agit d'un choix) :

\[\begin{aligned} K_1 &=f(t_n,u_n) \,\,\leftarrow\text{ (point de gauche)}\\ K_2 &=f(t_{n}+\frac{h}{2},u_n+\frac{h}{2}K_1) \,\,\leftarrow\text{ (prédiction à l'aide d'Euler progressive)}\\ K_3 &=f(t_{n}+\frac{h}{2},u_n+\frac{h}{2}K_2) \,\,\leftarrow\text{ (prédiction à l'aide de } K_2)\\ K_4 &=f(t_{n+1},u_n+hK_3) \,\,\leftarrow\text{ (prédiction à l'aide de } K_3) \end{aligned}\]

Ainsi, le schéma RK4 peut être écrit de la façon suivante :

\[ \left\{\begin{array}{rcl} u_{n+1} &=& u_n + \dfrac{h}{6}(K_1+2K_2+2K_3+K_4)\,,\\ u_0&=&y_0\,.\end{array}\right. \]