ICS CMS | R. Sauser (EPFL)

7.6 Stabilité et estimation de l'erreur

Stabilité

Nous allons étudier la stabilité d'un schéma numérique à partir d'un problème de Cauchy particulier :

\[ \left\{ \begin{array}{rcl} y'(t) &=&-\beta y\,, \text{ où }t\gt 0 \text{ et }\beta\in \mathbb{R}^+\,,\\ y(t_0) &=&y_0\,. \end{array} \right. \]

La solution à ce problème est la fonction

\[ y(t) = y_0\exp(-\beta t)\,. \]

Numériquement, dans le cadre d'une partition régulière de pas \(h\), le schéma d'Euler progressif s'écrit :

\[ u_{n+1} = u_n + h(-\beta u_n) = (1-\beta h)u_n\,,\text{ où }n=0,1,2,\ldots\,. \]

Ainsi,

\[ u_{n+1} = (1-\beta h)^{n+1}u_0\,,\text{ où }n=0,1,2,\ldots\,. \]

On remarque que, même si la solution du problème de Cauchy tend vers zéro lorsque \(t\) tend vers l'infini, la solution approchée lorsque \(n\) tend vers l'infini tend, en alternance, vers plus ou moins l'infini si \(u_0\ne 0\) et \(1-\beta h\lt -1\):

\[ (1-\beta h)^n\xrightarrow{n\rightarrow\infty}\pm\infty\,. \]

Dans ce cas particulier, le schéma d'Euler progressif n'est pas stable.

Pour éviter cette instabilité, il est nécessaire de respecter la condition de stabilité suivante :

\[ -1 \lt 1-\beta h ~~\Leftrightarrow~~ h\le\dfrac{2}{\beta}\,. \]

En appliquant le schéma d'Euler rétrograde au même problème de Cauchy particulier, il vient

\[ u_{n+1} = u_n + h(-\beta u_{n+1})~~\Leftrightarrow~~(1+\beta h)u_{n+1} = u_n \] \[ ~~\Leftrightarrow~~u_{n+1} = \dfrac{1}{1+\beta h}u_n \,,\text{ où }n=0,1,2,\ldots\,. \]

Ainsi,

\[ u_{n} = \dfrac{1}{(1+\beta h)^{n}}\,u_0\,,\text{ où }n=0,1,2,\ldots\,, \]

et on observe que, pour tout \(h\gt0\), on a

\[ \lim_{n\rightarrow \infty}{u_n} = 0\,. \]

Le schéma numérique d'Euler rétrograde est donc stable quelle que soit la valeur de \(h\).

Erreur absolue commise

L'erreur absolue commise correspond à la valeur absolue de la distance (différence) au moment (point) \(t_{n+1}\) entre la valeur exacte \(y_{n+1}\) et la valeur approchée \(u_{n+1}\) est donnée par \[ d_{n+1} = y_{n+1} - u_{n+1}\,. \]

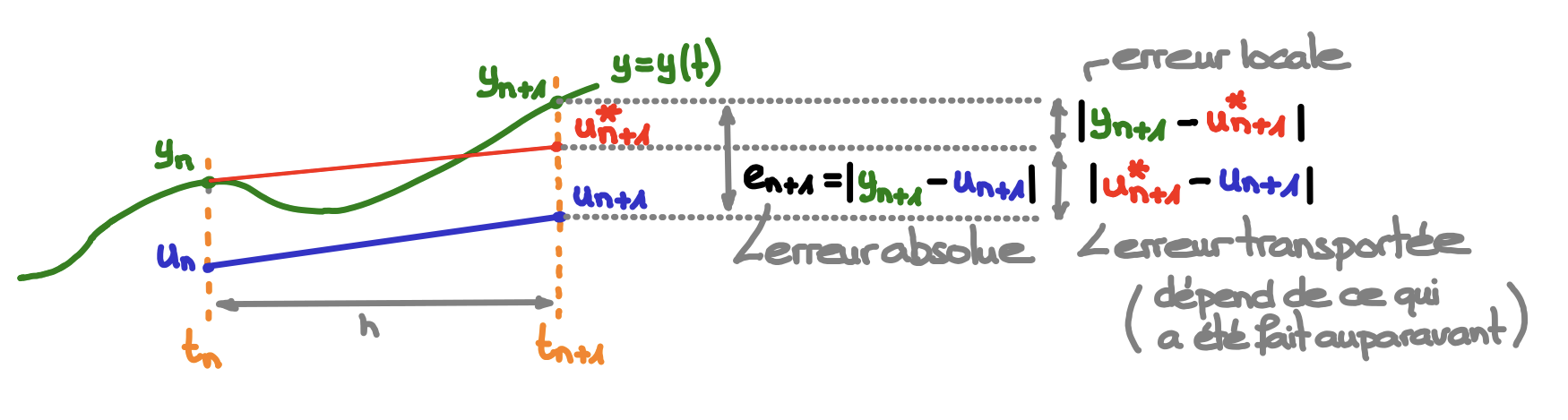
Deux types d'erreurs contribuent à l'erreur commise \(d_{n+1}\) :

les erreurs d'arrondi qui correspondent à des représentations inexactes des nombres dans l'ordinateur ;
les erreurs de troncature qui sont la somme d'une erreur locale et d'une erreur transportée : \[ d_{n+1} = \underbrace{(y_{n+1}-u_{n+1}^*)}_{\text{a)}} + \underbrace{(u_{n+1}^*-u_{n+1})}_{\text{b)}}\,, \] où
- l'erreur de troncature locale correspond à l'erreur commise sur une seule itération, à partir de la valeur exacte au pas précédent ;
- l'erreur de troncature transportée correspond aux erreurs accumulées depuis le temps initial.

La figure suivante illustre ces deux erreurs dans le cas de la méthode d'Euler progressive :