7.4 Champ de directions
Soient \(I\subset\mathbb{R}\) un intervalle réel et une EDO du premier
ordre à résoudre :
\[
y' = f(t,y)\,,
\]
où
-
\(t\) est la variable indépendante, \(t\in I\) ;
-
\(y=y(t)\) est une fonction solution cherchée et supposée
continûment différentiable sur \(I\), \(y:I\rightarrow\mathbb{R}\) ;
-
\(f(t,y)\) est une fonction donnée de \(t\) et
\(y\), \(f:I\times \mathbb{R}\rightarrow\mathbb{R}\).
En dessinant en tout point \((t,y)\) du domaine de définition
\(I\times \mathbb{R}\) de \(f\) un segment de pente \(f(t,y)\),
on obtient ce que l'on appelle le champ de directions de
l'EDO \(y'=f(t,y)\).
Une solution particulière \(y=y(t)\) de l'EDO est partout
tangente à ce champ de directions.
Ainsi, de manière plus concise, on peut donner la définition suivante :
Un champ de directions est une représentation graphique de
la fonction \(y'=f(t,y)\) avec \(t\) en abscisse et \(y\) en ordonnée.
Exemple:
Considérons la fonction
\[f(t,y)=2t
\]
et le problème de Cauchy associé
(sans préciser la condition initiale) :
\[
y' =2t\,.
\]
La solution à ce problème est la famille de fonctions
\[
y(t) = t^2 + A\,,\hskip 0.1cm \text{ où } A \text{ est une constante.}
\]
Le champ de directions de \(y'=2t\) permet de visualiser le comportement
des fonctions solutions avant même d'effectuer le moindre calcul
(analytique ou numérique) :
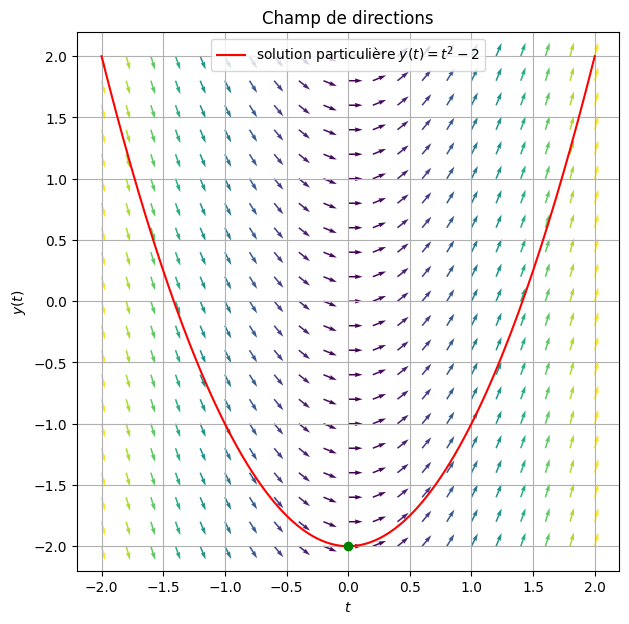
On remarque bien que, pour une valeur donnée de \(t\), la pente de la
fonction solution est la même pour toute valeur de \(y\) car \(y'\) ne
dépend pas explicitement de \(y\).
D'autre part, on vérifie que \(y(t)=t^2 -2\) est ici une solution du problème
de Cauchy considéré avec la condition initiale \(y(0)=-2\).
Cette solution particulière est en tout point de son graphe (dessiné
ici en rouge) tangente au champ de directions.
Dans le problème de Cauchy, le système évolue à partir de \(y_0\),
selon la dérivée \(y'\).
Le champ de directions est un outil qui permet de visualiser cette
évolution. Il permet en quelque sorte de
''visualiser'' l'EDO.